TU Wien:Algebra und Diskrete Mathematik VO (Karigl)/Prüfung 2017-01-27
Zur Navigation springen
Zur Suche springen
Beispiel 1[Bearbeiten | Quelltext bearbeiten]
Gegeben die Menge M={1, 2, ..., 7} und die Relation R mit aRb wenn a=b oder ggT(a,b)=2.
Gesucht:
- Vollständige Angabe der Menge R
- Graph G(R) für R
- Untersuche auf Reflexivität, Symmetrie, Antisymmetrie, Transitivität
- Ist R eine Äquivalenzrelation?
Beispiel 2[Bearbeiten | Quelltext bearbeiten]
Differenzengleichung 2. Ordnung
Beispiel 3[Bearbeiten | Quelltext bearbeiten]
Gegeben drei Vektoren aus
Bestimme Wert für sodass die Vektoren linear abhängig sind.
Beispiel 4[Bearbeiten | Quelltext bearbeiten]
Euklidischer Algorithmus:
- Nenne ein Beispiel mit zwei zweistelligen ganzen Zahlen.
- Wann bricht der Algorithmus ab?
- Wieso bricht der Algorithmus nach endlich vielen Schritten ab?
- Nenne zwei Anwendungsmöglichkeiten.
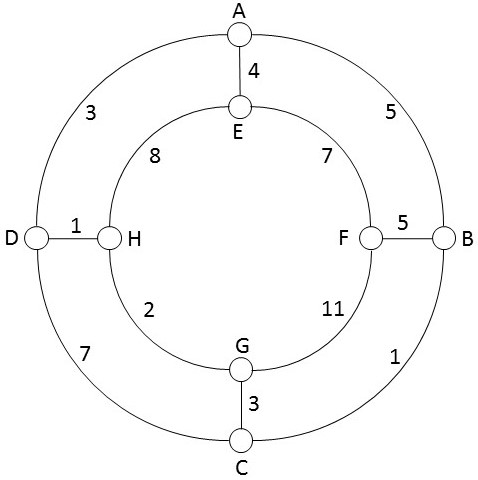
Beispiel 5[Bearbeiten | Quelltext bearbeiten]
Gegeben Netzwerk:
Hinweis: Die Werte für
- Knotenbezeichnungen und
- Kantenbewertungen
sind erfunden, jedoch für die Beantwortung der Single-Choice-Fragen irrelevant.
Single-Choice Fragen bzgl. dem gegebenen Netzwerk:
- Was ist der maximale Knotengrad?
- Wie viele Spannbäume sind im Graph enthalten?
- Wie viele Kanten hat ein Spannbaum?
- Hat der Graph ein minimales Gerüst?
- Ein minimales Gerüst ist minimal hinsichtlich welchem Kriterium?
- Kann zur Bestimmung eines minimalen Gerüsts der Algorithmus von Kruskal verwendet werden?