TU Wien:Algebra und Diskrete Mathematik VO (Karigl)/Prüfung 2019-05-03

Zeit: 100 Minuten

Aufgabe 1

Gegeben sei die rekursive Folge $x_{n+1}={\frac {x_{n}}{x_{n}(3^{n}-1)}},\quad (n\geq 1)$ mit Startwert ${\textstyle x_{1}={\frac {1}{2}}}$.

Berechnen Sie $x_{2},x_{3},x_{4}$ und $x_{5}$.

Beweisen Sie mittels vollständiger Induktion, dass Folgendes gilt:

$x_{n}={\frac {1}{3^{n}-1}}$

Notiz: Achtung, dieses Beispiel ist unlösbar. Angabe Falsch? Richtig lautet:

$x_{n}={\frac {1}{3^{n-1}-1}}$

Aufgabe 2

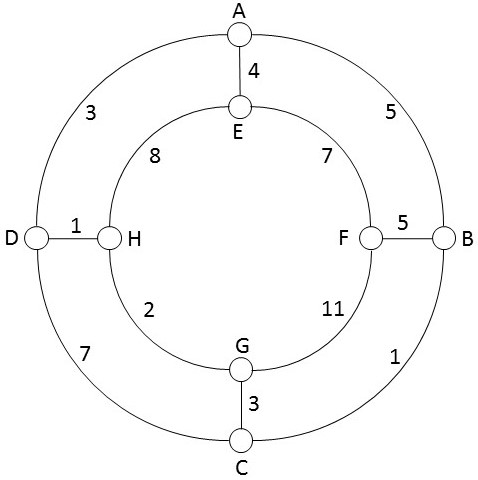
Man musste den minimalen Spannbaum eines Graphen bestimmen der genauso aussah wie der folgende nur mit anderen Kantenwerten.

Dies lässt sich sehr einfach mit dem Algorithmus von Kruskal bewerkstelligen.

Aufgabe 3

Lineares Gleichungssystem mit 3 Variablen und 3 Gleichungen auf Lösbarkeit untersuchen und gegenfalls alle Lösungen angeben (war nicht lösbar).

Aufgabe 4

Theorie zu Relationen:

• Definiere Reflexivität, Symmetrie, Antisymmetrie und Transitivität. Wofür stehen Äquivalenzrelation und Halbordnungsrelation? (Gebe jeweils ein Beispiel an)
• Beschreibe den Zusammenhang zwischen Äquivalenzrelation und Partition (kein Beweis notwendig).

Aufgabe 5

Multiple Choice zu einer 2019x2019 Matrize mit Determinante 2020. Die Matrix war nicht explizit angeben und man musste nur aufgrund ihrer Größe und Determinante auf Eigenschaften schließen.