TU Wien:Algebra und Diskrete Mathematik VU (diverse)/Übungen 2023W/Beispiel 282

Man bestimme die kleinste transitive Relation $R$ , die $G_{3}$ (als Relation aufgefaßt) enthält.
Anm: Angabe ist nicht eindeutig, siehe Alternativen.

Anm 071123: Angabe wurde im WS07 offenbar auf "umfasst" umgeändert, was aber nicht wirklich klarer ist.

Dieses Beispiel hat einen unbekannten Lösungsstatus. Bitte editiere diese Seite und schreibe den dir bekannten Status ins Beispiel. Die möglichen Werte sind hier: Vorlage:Beispiel dokumentiert. Führe folgende Änderung durch:

{{Beispiel|1=
Angabetext
}}

oder

{{Beispiel|
Angabetext
}}

zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)

{{Beispiel|status=solved|1=
Angabetext
}}

Wäre dann nach der Definiton aRb und bRc => aRc jede Verbindung dreier durch gerichtete Kanten verbundene Knoten:

z.b. (4,1,7), (1,7,6), (7,6,1), (4,3,2), (3,2,1), ...

Hapi

PS: Die Lösung bei Urbanek war dieselbe wie von jurewitsch. Habe die Definition der transitiven Relation nicht vollständig berücksichtigt.

Andere Meinung: Transitiv bedeutet: aRb und bRc => aRc

also müsste doch anhand des obigen Bsps zum Beispiel von 4 nach 7 ein Pfeil sein. Ist aber nicht. ein Beispiel für eine transitive Relations wäre meiner Meinung nach zum Beispiel (2,4,1). Weil 2R4 und 4R1 ABER AUCH: 2R1 und somit wäre das dann transitiv. Wenn wer weitere findet, bitte posten, ich kann nur die eine entdecken.

poseidon

Lösung von jurewitsch[Bearbeiten | Quelltext bearbeiten]

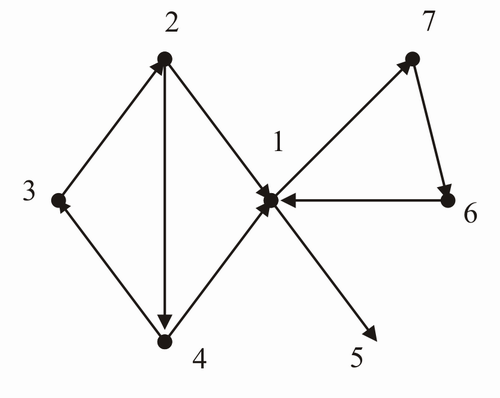
Transitive Relation: $\forall x,y,z:xRy\wedge yRz\Rightarrow xRz$ .

Der Graph $G_{3}$ als Relation: Die Menge $G$ ={1,2,3,4,5,6,7} und mit ( $x\in G$ , $y\in G$ ) $\in$ R:

(1,7),(1,5)
(2,1),(2,4)
(3,2)
(4,3)(4,1)
(6,1)
(7,6)

also (x,y) $\in$ R, wenn es eine gerichtete Kante von x nach y gibt.

Diese Paare sollen jetzt alle schon in der gesuchten transitiven Relation sein. Natürlich muss man aber dann einige dazu geben, damit das transitiv wird.

Zum Beispiel: Da (1,7) und (7,6) Element aus der neuen Relation muss auch (1,6) Element der neuen Relation sein.

Gesamt ergibt das folgende Relation: M: {1,2,3,4,5,6,7}, R:

{(1,7),(1,5),(1,6),(1,1)
 (2,1),(2,7),(2,5),(2,6),(2,4),(2,3),(2,2)
 (3,2),(3,1),(3,7),(3,5),(3,6),(3,4),(3,3)
 (4,3),(4,1),(4,2),(4,7),(4,5),(4,6),(4,7)
 (6,1),(6,7),(6,5),(6,6)
 (7,6),(7,1),(7,5),(7,7)}

Alternativen[Bearbeiten | Quelltext bearbeiten]

Die Angabe kann auf zwei verschiedene Arten aufgefaßt werden:

Man bestimme die kleinste transitive Relation $R$ , die den Graphen $G_{3}$ enthält, also $G_{3}\subseteq R$ .
Man bestimme die kleinste transitive Relation $R$ , die in $G_{3}$ enthalten ist, also $R\subseteq G_{3}$ .