TU Wien:Algorithmen und Datenstrukturen VU (Szeider)/Übungen 2019S

Übung 1

Aufgabe 1.1

Gegeben ist folgendes Stable Matching Problem.

   1. 2. 3. 4.      1. 2. 3. 4.
A  L  M  N  O    L  B  C  A  D
B  L  N  M  O    M  D  A  B  C
C  M  O  L  N    N  A  B  C  D
D  L  O  N  M    O  A  B  D  C

Aufgabe 1.2

Gegeben sind die folgenden Funktionen:

$f(n)=2^{-n}+(4n-3n^{2})^{2}+7n^{3}$

$g_{1}(n)={\begin{cases}3n^{3n}&{\text{falls n gerade und prim}}\\\log _{3}(n^{7})\cdot 9n^{3}&{\text{sonst}}\end{cases}}$

$g_{2}(n)={\sqrt[{3}]{\frac {n^{1}4-n^{8}}{n^{2}}}}$

$g_{3}(n)={\begin{cases}(n^{2}+1)^{3}&{\text{falls n gerade}}\\{\frac {5n^{2}}{\sqrt[{3}]{\frac {1}{27n^{6}}}}}&{\text{sonst}}\end{cases}}$

Kreuzen Sie in der folgenden Tabelle die zutreffenden Felder an und begründen Sie Ihre Antworten (formaler Beweis ist nicht notwendig):

f(n) ist in	Θ(.)	O(.)	Ω(.)	keines
$g_{1}(n)$			X
$g_{2}(n)$	X	X	X
$g_{3}(n)$		X

Hinweis: Setzen Sie statt dem Punkt die entsprechende Funktion (g1, g2 bzw. g3) ein. Beispielsweise ist die Zelle links oben als "f(n) ist in Θ(g1(n))" zu lesen.

Aufgabe 1.3

Fügen Sie bei den folgenden Aufwandsabschätzungen die entsprechenden Symbole Θ, O oder Ω in die dafür vorgesehenen Kästchen ein:

$n^{n+1}=$	Ω	$(n^{n})$
$16^{n}=$	Θ	$(2^{4n})$
${\sqrt[{3}]{n^{5}}}=$	O	$(n^{2})$
$(n-1)!=$	O	$(n!)$
$n^{11}\cdot 3^{n}=$	O	$(4^{n})$
$\log _{3}n=$	Θ	$(\ln n)$
$\log {\sqrt {3}}=$	Θ	$(1)$
${\sqrt[{3}]{n^{4}}}=$	Ω	$({\sqrt[{4}]{n^{3}}})$

Ist die Lösung in jedem Fall eindeutig? Begründen Sie ihre Antwort.

Aufgabe 1.4

(a) Beweisen oder widerlegen Sie, dass für die folgende Funktion f(n) die Beziehung $f(n)=\Omega (n^{4}\log _{2}n)$ gilt:

$f(n)={\begin{cases}n^{4}\log _{2}n^{5}+1000\cdot n^{3},&{\text{falls n eine Primzahl ist}}\\{\sqrt {n^{6}}}\cdot n\log _{3}n-{\frac {2}{n^{2}}}&{\text{sonst}}\end{cases}}$

(b) Beweisen oder widerlegen Sie, dass

${\binom {2n}{3}}=\Theta (n^{3})$

gilt.

Hinweis: Bedenken Sie, dass für einen Beweis gegebenenfalls auch geeignete Werte für die Konstanten c1, c2 und n0 angegeben werden müssen.

Aufgabe 1.5

Bestimmen Sie die Laufzeiten der unten angegebenen Algorithmen in Abhängigkeit von n in Θ-Notation. Verwenden Sie hierfür möglichst einfache Terme.

x = 4*n
y = 0
while x > 0
    x = ⌊x/2⌋
    for i = 1,...,n
        y = y + x*i

i = 1
x = 1
while i < n
    a = 4*i
    for j = a, ..., 1
        x = x + j
    i = a/2

Aufgabe 1.6

Bestimmen Sie die Laufzeiten und die Werte der Variablen a und b nach der Ausführung der unten angegebenen Algorithmen in Abhängigkeit von n in Θ-Notation. Verwenden Sie hierfür möglichst einfache Terme.

a = 1
b = 1
for c = 1, ... 1/2 log_2 n
    a = 4a
    b = c
    a = ⌊a/2⌋
i = 2^(2b)
while i > 1
    i = ⌊i/2⌋

a = n^3
b = 1
while a > 1
    b = b + 1
    c = n
    do
        a = ⌊b/2⌋
        c = 2c/n
        b = b*n
    while c >= n

Aufgabe 1.7

Zeigen Sie, dass $f(n)+g(n)=O(\max(f(n),g(n)))$ gilt.

Hinweis: Verwenden Sie die Definitionen aus den Folien.

Übung 2

Aufgabe 2.1

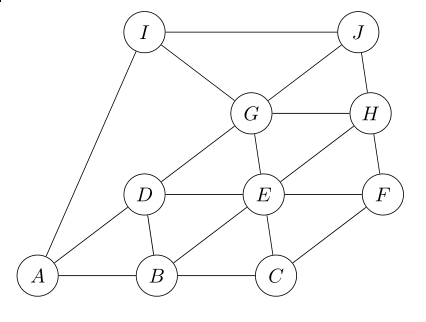
Führen Sie auf dem nachfolgenden Graphen die Breiten- und Tiefensuche entsprechend den Algorithmen in den Vorlesungsfolien durch. Geben Sie dabei jeweils eine gültige Reihenfolge an, in der die Knoten besucht werden.

Zeichnen Sie zusätzlich den Tiefen- und Breitensuchbaum. Eine Kante v → w in diesen Bäumen drückt aus, dass Knoten w von Knoten v aus entdeckt wurde.

Verwenden Sie jeweils A als Startknoten. Haben Sie die Wahl zwischen mehreren Knoten gehen Sie alphabetisch vor.

Aufgabe 2.2

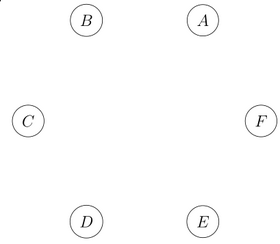
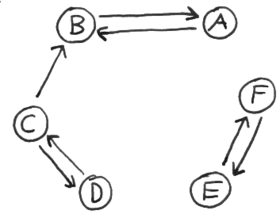
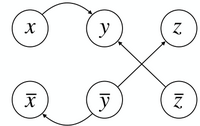
Zeichnen Sie gerichtete Kanten zwischen den gegebenen Knoten ein, so dass der resultierende, gerichtete Graph exakt zwei schwache und drei starke Zusammenhangkomponenten hat. Geben Sie zusätzlich die Komponenten an.

starke Zusammenhangkomponenten: (A,B), (C,D), (E,F)

schwache Zusammenhangkomponenten: (A,B,C,D), (E,F)

Aufgabe 2.3

Beantworten Sie folgende Fragen zu Graphen: (a) Wir nehmen eine kleine Modifikation an dem in der Vorlesung vorgestellten Pseudocode für Tiefensuche (Foliensatz Graphen) vor. Als letzte Zeile der Funktion DFS1 wird (nach der foreach-Schleife) Discovered[u] <- false eingefügt.

Wie oft tritt nun der Fall ein, dass DFS1 keinen weiteren Rekursionsaufruf tätigt, wenn dieser modifizierte Algorithmus (also DFS mit beliebigen Startknoten) auf den vollständigen ungerichteten Graphen (d.h. von jedem Knoten existiert eine Kante zu allen anderen Knoten) mit 15 Knoten ausgeführt wird?

(b) Sei G ein vollständiger gerichteter Graph (d.h. von jedem Knoten existiert eine gerichtete Kante zu allen anderen Knoten) mit 20 Knoten. Wie viele Kanten müssen mindestens entfernt werden, sodass zumindest eine topologische Sortierung existiert?

Aufgabe 2.4

Konstruieren Sie einen schlichten, ungerichteten, zusammenhängenden Graphen mit mehr als sechs Knoten, der mindestens drei Knoten mit Grad drei enthält. Wählen Sie den Graphen so, dass es (für einen von Ihnen gewählten Startknoten) für die Breiten- und Tiefensuche (zumindest) eine identische Abarbeitungsreihenfolge der Knoten gibt.

Aufgabe 2.5

Wir bezeichnen einen ungerichteten Graphen $G=(V,E)$ als bipartit, wenn sich dessen Knoten in zwei Mengen $V_{1}$ und $V_{2}$ aufteilen lassen, für die gilt: $V_{1}\cup V_{2}=V$, $V_{1}\cap V_{2}=\emptyset$ und $E\subseteq V_{1}\times V_{2}$.

Finden Sie einen Algorithmus, der in linearer Laufzeit bestimmt, ob ein gegebener Graph bipartit ist. Entwickeln Sie eine Lösung in detailliertem Pseudocode und argumentieren Sie, dass der Algorithmus korrekt ist und die geforderte Laufzeitschranke gilt.

Aufgabe 2.6

Gegeben sind n Programme $P_{1},\dots ,P_{n}$, welche auf einer Festplatte mit einer Kapazität von D Megabyte gespeichert werden sollen. Der Platz, der für ein Programm $P_{i}$ benötigt wird, ist s i Megabyte. Nehmen Sie an, dass es nicht möglich ist, alle Programme gleichzeitig auf der Festplatte zu speichern (es gilt also ${\textstyle D<\sum _{i=1}^{n}s_{i}}$).

(a) Maximiert ein Greedy-Algorithmus, der die Programme in aufsteigender, nach Größe geordneter, Reihenfolge auswählt, die Anzahl der zu speichernden Program- me? Geben Sie einen Beweis oder ein Gegenbeispiel an.

(b) Maximiert ein Greedy-Algorithmus, der die Programme in absteigender, nach Größe geordneter, Reihenfolge auswählt, die Auslastung der Festplatte? Geben Sie einen Beweis oder ein Gegenbeispiel an.

Aufgabe 2.7

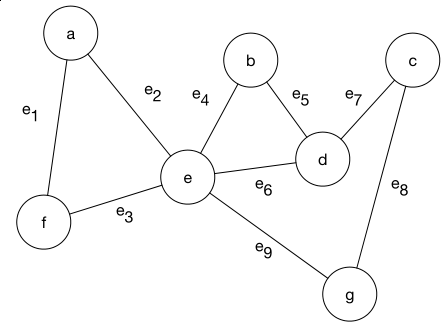
Bestimmen Sie den minimalen Spannbaum für folgenden Graphen. Verwenden Sie dazu den Algorithmus von Prim und beginnen Sie bei Knoten F . Haben Sie danach die Wahl zwischen mehreren Knoten gehen Sie alphabetisch vor. Geben Sie nach jedem Schleifendurchlauf den aktuell ausgewählten Knoten, den Inhalt der Priority Queue Q, die Knotenmenge S und das Gewicht des aktuellen Spannbaums an.

Übung 3

Aufgabe 3.1

Gegeben ist der folgende Min-Heap:

(a) Fügen Sie die Elemente 8 und 2 in der angegebenen Reihenfolge in den Min-Heap ein. Stellen Sie nach jedem Einfügevorgang den resultierenden Heap als Baum dar. Erklären Sie dabei, wie Sie Heapify-up korrekt anwenden.

(b) Entnehmen Sie aus dem in Aufgabe 1 gegebenen Min-Heap drei Mal das kleinste Element. Stellen Sie nach jedem Löschvorgang den resultierenden Heap als Baum dar. Erklären Sie dabei, wie Sie Heapify-down korrekt anwenden.

Anmerkung für Interessierte: Mithilfe von Heaps können Arrays sortieren werden. Ein bekannter Sortieralgorithmus, der einen Heap als zentrale Datenstruktur verwendet, ist Heapsort.

Aufgabe 3.2

Gegeben ist das Array [7, 3, 4, 6, 2, 9, 1].

(a) Führen Sie Mergesort auf dem oben gegebenen Array aus und geben Sie Zwischenschritte in Form eines Ablaufdiagrammes wie im Foliensatz Divide-and-Conquer an.

(b) Führen Sie Quicksort auf dem oben gegebenen Array aus. Wählen Sie stets das erste Element als Pivot-Element aus und implementieren Sie den Schritt des Aufteilens so, dass die Elemente einer Subfolge immer in derselben Reihenfolge angeordnet werden wie in der Originalfolge. Geben Sie die Zwischenschritte wie im Foliensatz Divide-and-Conquer an.

Aufgabe 3.3

Ein Vertreter der linearen Sortieralgorithmen ist Radixsort. Die Grundidee basiert darauf, dass die zu sortierenden Wörter oder Zahlen mehrmals in Fächer (Buckets) verteilt werden, sodass nach der letzten Verteilung die Elemente in sortierter Reihenfolge entnommen werden können.

Finden Sie zunächst mithilfe einer Internet- und/oder Literaturrecherche heraus, wie Radixsort genau funktioniert.

(a) Sortieren Sie die folgenden Zahlen aufsteigend mithilfe von Radixsort:

447, 415, 683, 437, 613, 645, 435

 3    5    7
683  415  447
613  645  437
     435

683, 613, 415, 645, 435, 447, 437

 1    3    4    8
613  435  645  683
415  437  447

613, 415, 435, 437, 645, 447, 683

 4    6
415  613
435  645
437  683
447

415, 435, 437, 447, 613, 645, 683

(b) Handelt es sich bei Radixsort um einen Divide-and-Conquer-Algorithmus? Begründen Sie Ihre Antwort.

Nur wenn man bei der höchstwertigen Stelle (MSD) beginnt.

Aufgabe 3.4

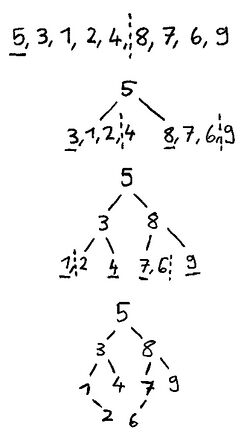
Gegeben ist die preorder-Traversierung eines binären Suchbaumes:

5, 3, 1, 2, 4, 8, 7, 6, 9

Rekonstruieren Sie mithilfe dieser Information den binären Suchbaum nach dem Divide-and-Conquer-Prinzip. Geben Sie dabei jeweils den aktuellen Zustand des Baumes nach jedem Teile-Schritt an.

• Preorder: Wurzel, linker Unterbaum, rechter Unterbaum
• binärer Suchbaum: jeder Knoten im linken Unterbaum muss kleiner und jeder Knoten im rechten Unterbaum muss größer sein als der aktuelle Knoten

Aufgabe 3.5

Schreiben Sie einen Algorithmus in detailliertem Pseudocode auf, der die Balance für jeden Knoten eines AVL-Baumes ermittelt. Ihre Funktion soll als Argu- ment einen Knoten des Baumes akzeptieren und mit dem Wurzelknoten des Baumes aufgerufen werden.

Jeder Knoten x des Baumes hat folgende Attribute:

• x.key: Schlüssel von x
• x.left / x.right: Verweis auf linkes / rechtes Kind von x (null, wenn nicht vorhanden)
• x.parent: Verweis auf den Elternknoten von x (null, wenn Wurzel)
• x.height: Höhe des Teilbaumes mit Wurzelknoten x
• x.balance: die Balance des Knotens x

Nach Ausführung Ihres Pseudocodes soll das Attribut x.balance für jeden Knoten x des Baumes korrekt berechnet sein. Gehen Sie davon aus, dass Sie das Attribut x.height für jeden Knoten zuerst neu berechnen müssen, bevor Sie darauf in Ihrem Code (erstmalig) zugreifen.

Aufgabe 3.6

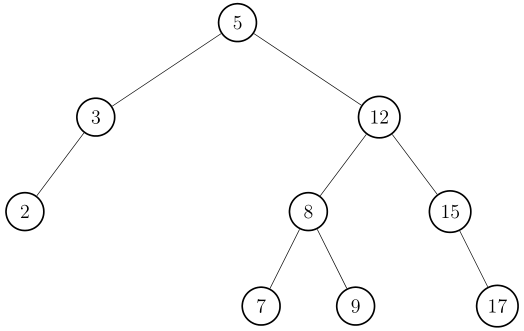
Gegeben ist folgender AVL-Baum:

(a) Fügen Sie zuerst den Schlüssel 1 und dann 11 in den oben gegebenen AVL-Baum ein. Falls notwendig, so rebalancieren Sie den Baum nach jedem Einfügen mit einer geeigneten Rotationsoperation (siehe Foliensatz Suchbäume), um wieder einen gültigen AVL-Baum zu erhalten. Markieren Sie dabei den unbalancierten Knoten mit maximaler Tiefe.

(b) Löschen Sie aus dem in Aufgabe 6 gegebenen AVL-Baum die Schlüssel 2 und 5 in dieser Reihenfolge. Falls notwendig, so rebalancieren Sie den Baum nach jedem Löschvorgang mit einer geeigneten Rotationsoperation (siehe Foliensatz Suchbäume), um wieder einen gültigen AVL-Baum zu erhalten. Markieren Sie dabei den unbalancierten Knoten mit maximaler Tiefe.

Aufgabe 3.7

Lösen Sie folgenden Unteraufgaben zu B-Bäumen.

(a) Fügen Sie die Elemente der Folge

1, 3, 6, 8, 11, 14, 20, 40

in dieser Reihenfolge in einen anfangs leeren B-Baum der Ordnung 3 ein. Zeichnen Sie den B-Baum jeweils vor und nach jeder Reorganisationsmaßnahme und geben Sie den endgültigen B-Baum an.

(b) Geben Sie den B-Baum an, der durch Löschen der Schlüssel 11 und 8 (in dieser Reihenfolge) aus dem Baum von Unteraufgabe (a) entsteht. Stellen Sie den B-Baum nach jedem Zwischenschritt dar und führen Sie gegebenenfalls geeignete Reorgansi- sationsmaßnahmen durch.

Übung 4

Aufgabe 4.1

Die Wahrscheinlichkeit, dass es nach dem Einfügen von n gleichverteilt zufällig gezogenen Elementen in eine Hashtabelle der Größe m mit uniformer Hashfunktion zumindest eine Kollision gibt, ist näherungsweise:

$p(n,m)\approx 1-\exp \left(-{\frac {n^{2}}{2m}}\right)$

(a) Wie groß muss m nach dieser Näherung gewählt werden, damit nach dem Einfügen von n = 23 Elementen mit 50% Wahrscheinlichkeit eine Kollision entsteht?

${\begin{aligned}0{,}5&=1-\exp \left(-{\frac {23^{2}}{2m}}\right)\\0{,}5&=\exp \left(-{\frac {23^{2}}{2m}}\right)\\\ln(0{,}5)&=-{\frac {23^{2}}{2m}}\\m&=-{\frac {23^{2}}{2\ln(0{,}5)}}\approx 381{,}59\approx 382\\\end{aligned}}$

(b) Betrachte eine uniforme Hashfunktion h und eine Hashtabelle der Größe $m=2^{512}$. Sei nun k ein Schlüssel und h(k) sein dazugehöriger Hashwert. Wie viele Schlüssel muss ein Angreifer nach der erwähnten Näherung durchprobieren, um mit 50% Wahrscheinlichkeit einen anderen Schlüssel $k'\neq k$ mit gleichem Hashwert $h(k')\neq h(k)$ zu finden?

${\begin{aligned}0{,}5&=1-\exp \left(-{\frac {n^{2}}{2^{512}}}\right)\\\ln(0{,}5)&=-{\frac {n^{2}}{2^{512}}}\\n^{2}&=-2^{512}\ln(0{,}5)\\n&={\sqrt {-2^{512}\ln(0{,}5)}}=2^{256}{\sqrt {-\ln(0{,5})}}\approx 9.64\cdot 10^{76}\end{aligned}}$

Aufgabe 4.2

Gegeben seien folgende geordnete natürliche Zahlen:

[19, 16, 11, 9, 20, 0, 3]

Fügen Sie diese in der vorgegebenen Ordnung jeweils in folgende Varianten von anfangs leeren Hashtabellen der Größe m = 9 ein und stellen Sie die einzelnen Schritte und die finale Belegung dar. Geben Sie weiters jeweils die durchschnittliche Laufzeit einer erfolgreichen Suche eines Elements an.

(a) Verkettung der Überläufer mit $h(k)=k\mod m$.

h(k) = k mod 9

h(19)=1, h(16)=7, h(11)=2, h(9)=0, h(20)=2, h(0)=0, h(3)=3

0	1	2	3	4	5	6	7	8
9 0	19	11 20	3				16

durchschnittliche Laufzeit für erfolgreiche Suche: ${\frac {5+2\cdot 2}{7}}={\frac {9}{7}}$

Für das Sondieren (quadratisch und Double-Hashing) gilt $i=0,1,\dots ,m-1$.

(b) Quadratisches Sondieren mit

• $h(k)=(h'(k)+c_{1}i+c_{2}i^{2})\mod m$
• $h'(k)=\lfloor m(kA-\lfloor kA\rfloor )\rfloor$
• $c_{1}={\tfrac {1}{2}},\ c_{2}={\tfrac {1}{2}}$ und $A=({\sqrt {5}}-1)/2$.

(c) Double-Hashing mit

• $h(k)=(h_{1}(k)+ih_{2}(k))\mod m$
• $h_{1}(k)=k\mod m$
• $h_{2}(k)=1+(k\mod 5)$

h1 = k mod 9

h2 = (k mod 5) + 1

• h1(19)=1, h1(16)=7, h1(11)=2, h1(9)=0
• h1(20)=2 (Kollision) → 2+1=3
• h1(0)=0 (Kollision) → 0+1=1 (Kollision) → 0+2=2 (Kollision) → 0+3=3 (Kollision) → 0+4=4
• h1(3)=3 (Kollision) → 3+4=7 (Kollision) → (3+8)mod 9 = 2 (Kollision) → (3+12) mod 9 = 6

0	1	2	3	4	5	6	7	8
9	19	11	20	0		3	16

durchschnittliche Laufzeit für erfolgreiche Suche: ${\frac {4+2+5+4}{7}}={\frac {15}{7}}$

Aufgabe 4.3

(a) Die Funktion sort() der C++ Standard Library wird üblicherweise mit einer Kombination mehrerer Sortieralgorithmen namens Introsort implementiert. Finden Sie heraus, welche Algorithmen bei Introsort kombiniert werden. Erklären Sie kurz wie diese Kombination funktioniert und welche Vorteile sie bietet.

(b) Die Funktion stable sort() der C++ Standard Library muss laut Spezifikation stabil sein und eine Worst Case Laufzeit von n log(n) aufweisen (falls ausreichend zusätzlicher Speicher zur Verfügung steht). Mit welchem Sortieralgorithmus, den Sie aus der Vorlesung kennen, können Sie diese Spezifikation erfüllen?

(c) Sie finden den Sourcecode für die OpenJDK Implementierung der Datenstruktur HashMap unter: http://hg.openjdk.java.net/jdk8/jdk8/jdk/file/687fd7c7986d/src/share/classes/java/util/HashMap.java In dieser Implementierung wird die verkettete Liste der Überläufer für einen Hashwert in einen Suchbaum umgewandelt, falls sie zu lang wird. Finden Sie heraus, beiwelchen Operationen und unter welchen Bedingungen ein Suchbaum wieder zu einer verketteten Liste umgewandelt wird.

Aufgabe 4.4

Sei P ein Ja/Nein-Problem für Instanzen mit Größe n. Nehmen Sie an, dass es eine Reduktion von P auf ein Problem Q gibt, die $O(n^{2})$ Zeit benötigt. Nehmen Sie weiterhin an, dass Problem Q NP-vollständig ist. Geben Sie für die folgenden Aussagen an, ob sie wahr oder falsch sind oder ob keine Aussage möglich ist. Begründen Sie Ihre Antwort.

(a) P ist in NP.

Wahr, da Q in NP liegt und P polynomiell auf Q reduziert werden kann.

(b) P ist NP-schwer.

Keine Aussage möglich. P könnte auch in P liegen.

(c) P ist NP-vollständig.

Keine Aussage möglich. Ein Problem kann nur dann NP-vollständig sein, wenn es NP-schwer ist.

Nehmen Sie nun zusätzlich an, dass Sie das Problem Q in Zeit O(m 2 log(m)) lösen können, wobei m die Eingabegröße einer Instanz von Q ist.

(d) Bedeutet dies, dass jede Instanz von P in polynomieller Zeit gelöst werden kann? Begründen Sie Ihre Antwort.

(e) Bedeutet dies, dass jede Instanz von Sat in polynomieller Zeit gelöst werden kann? Begründen Sie Ihre Antwort.

(f) Geben Sie eine obere Schranke für die Laufzeit (eines optimalen Algorithmus) für das Problem P an und begründen Sie Ihre Antwort kurz.

(g) Bedeutet dies, dass jede Instanz von Sat in O(n 8 ) gelöst werden kann? Begründen Sie Ihre Antwort.

Aufgabe 4.5

Aufgabe 5. Im Folgenden sind verschiedene Probleme mit einem Zertifikat und einem Zertifizierer gegeben. Überlegen Sie sich, ob das Zertifikat und der Zertifizierer geeignet sind um zu zeigen, dass das gegebene Problem in NP ist. Begründen Sie Ihre Antwort.

(a)

• Problem: Gegeben sei ein Graph G. Ist G 3-färbbar?
• Zertifikat: Eine 3-Färbung von G.
• Zertifizierer: Überprüfe, ob keine zwei benachbarten Knoten die selbe Farbe haben.

Geeignet, da Zertifikat polynomielle Länge hat und Zertifizierung in Polynomialzeit möglich ist.

(b)

• Problem: Ein Vertex Cover ist minimal, falls es kein Vertex Cover mit weniger Knoten gibt. Gegeben sei ein Graph G und ein Knoten v. Gibt es ein minimales Vertex Cover in dem v enthalten ist?
• Zertifikat: Ein minimales Vertex Cover C das v enthält.
• Zertifizierer: Überprüfe, ob C ein minimales Vertex Cover ist und ob v in C enthalten ist.

Ungeeignet, da kein Algorithmus (Zertifizierer) bekannt ist, der ein minimales Vertex Cover in Polynomialzeit findet.

(c)

• Problem: Gegeben sei ein gewichteter Graph G, Knoten u und v sowie eine natürliche Zahl k. Gibt es einen Pfad von u nach v der Länge k oder kürzer?
• Zertifikat: Ein leerer String.
• Zertifizierer: Überprüfe mit Hilfe des Dijkstra Algorithmus, ob es einen Pfad von u nach v der Länge k oder kürzer gibt.

Geeignet, da Dijkstra einen kürzesten Pfad findet und mit einer Laufzeit von O(m+n log n) implementiert werden kann.

(d)

• Problem: Gegeben sei ein ganzzahliges Polynom p(x). Hat p keine Nullstellen?
• Zertifikat: Eine Nullstelle $x_{0}$ von p.
• Zertifizierer: Überprüfe, ob $p(x_{0})=0$.

Ungeeignet, da es sich um Nein-Instanzen handelt.

(e)

• Problem: Gegeben sei ein Graph G und eine Zahl k. Hat G einen Minimal Spanning Tree T, sodass es keinen Knoten in T gibt, dessen Grad größer als k ist?
• Zertifikat: Ein MSP T, sodass es keinen Knoten in T gibt, dessen Grad größer als k ist.
• Zertifizierer: Überprüfe, ob T ein Spanning Tree ist und es keinen Knoten in T gibt, dessen Grad größer als k ist. Berechne einen MST T' via Prim/Kruskal und überprüfe, ob das Gewicht von T' gleich dem Gewicht von T ist.

Geeignet. Überprüfung auf Spannbaum mit Tiefensuche in O(n+m). MST mit Kruskal berechnen: O(m log n)

Aufgabe 4.6

Das komplett vernetzter Subgraph Problem ist wie folgt definiert: Gegeben sei ein Graph G = (V, E) und eine natürliche Zahl k. Existiert ein komplett vernetzter Subgraph der Größe k in G, d.h., gibt es k Knoten in G, die alle paarweise adjazent sind?

Geben Sie eine polynomielle Reduktion von Independent Set auf komplett vernetzter Subgraph an und begründen Sie die Korrektheit der Reduktion.

Wenden Sie Ihre Reduktion auf die folgende Independent Set Instanz an: Kreis C 5 mit 5 Knoten {a, b, c, d, e} und k = 3.

Übung 5

Aufgabe 5.1

Betrachten Sie das im Allgemeinen NP-schwere Problem den größten komplett vernetzten Subgraphen in einem gegebenen Graphen $G=(V,E)$ zu finden, d.h. einen Teilgraphen $G'=(V',E')$ mit maximal großer Teilmenge $V'\subseteq V$ , sodass $E'=\{(u,v)\mid u,v\in V'\}\subseteq E$.

Entwerfen und beschreiben Sie einen polynomiellen Algorithmus in Pseudocode, der das Problem für den Spezialfall löst, dass G ein Intervallgraph ist. Gehen Sie dabei davon aus, dass die Eingabe eine Menge I von (nicht leeren) Intervallen ist und in I alle Intervallgrenzen paarweise verschieden sind. Die Ausgabe soll wiederum eine Teilmenge $I'\subseteq I$ sein, die einem größten komplett vernetzten Subgraphen entspricht.

Begründen Sie die Korrektheit Ihres Algorithmus und geben Sie die asymptotische Laufzeit an.

Aufgabe 5.2

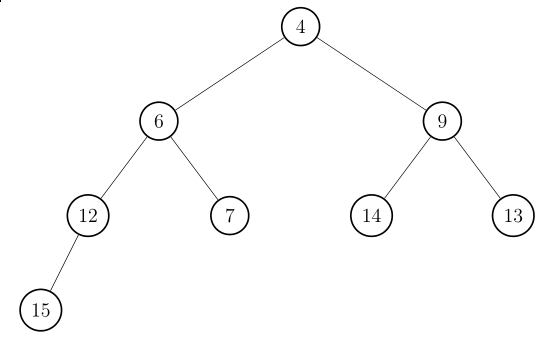
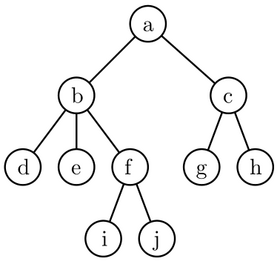
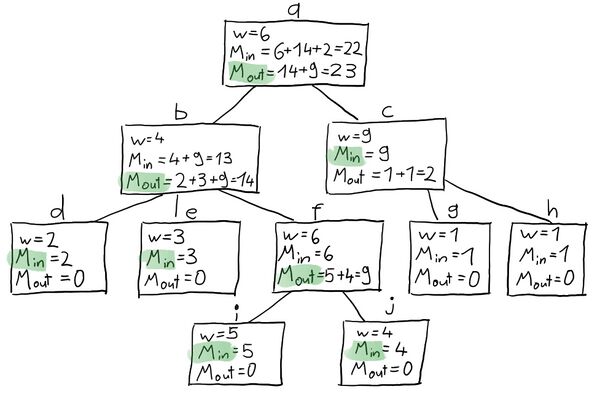
Führen Sie den Algorithmus zur Berechnung des Independent Sets mit maximalem Gewicht für den gegebenen Baum mit den Knotengewichten aus der Tabelle aus. Bestimmen Sie zu jedem Knoten u den Wert $M_{\text{in}}[u]$ und den Wert $M_{\text{out}}[u]$. Geben Sie das berechnete gewichtete Independent Set und sein Knotengewicht an.

Handelt es sich bei der Lösung auch um ein maximales Independent Set (bezüglich Kardinalität)? Begründen Sie Ihre Antwort.

Knoten   a b c d e f g h i j
Gewicht  6 4 9 2 3 6 1 1 5 4

Independent Set = {c, d, e, i, j}

Nicht maximal bezüglich Kardinalität (es gibt 6 Blätter).

Aufgabe 5.3

2-SAT bezeichnet eine Variante des Erfüllbarkeitsproblems aussagenlogischer Formeln (SAT), bei der jede Klausel der Eingabeformel genau zwei Literale enthält. Wir definieren nun folgenden Graphen:

Sei $F=(l_{1}^{1}\lor l_{1}^{2})\land \cdots \land (l_{m}^{1}\lor l_{m}^{2})$ eine KNF-Formel mit genau zwei Literalen in jeder Klausel, $var(F)$ die Menge der in F vorkommenden Variablen und ${\bar {\bar {x}}}=x$. Der Implikationsgraph (implication graph) der Formel F ist der gerichtete Graph $G=(V,E)$ mit Knotenmenge $V=\{x,{\bar {x}}\mid x\in var(F)\}$ und Kantenmenge $E=\{({\overline {l_{i}^{1}}},l_{i}^{2}),({\overline {l_{i}^{2}}},l_{i}^{1})\mid 1\leq i\leq m\}$.

Der Implikationsgraph zu $F=({\bar {x}}\lor y)\land (y\lor z)$ sieht zum Beispiel so aus:

Beantworten Sie die folgenden Fragen bzw. lösen Sie die folgenden Aufgaben:

(a) Geben Sie eine unerfüllbare 2-SAT-Instanz und den dazugehörigen Implikationsgraphen G an. Markieren Sie die starken Zusammenhangskomponenten von G. Was fällt Ihnen auf?

(b) Angenommen, eine starke Zusammenhangskomponente enthält die Literale l und l' 0, und τ ist eine erfüllende Belegung. Was kann man über die Wahrheitswerte τ(l) und τ(l') aussagen?

(c) Was bedeutet es, wenn eine starke Zusammenhangskomponente ein Literal $l$ und dessen Negation ${\bar {l}}$ enthält?

(d) Angenommen, eine Menge L von Literalen ist eine starke Zusammenhangskomponente von G. Zeigen Sie, dass die Menge ${\bar {L}}=\{{\bar {l}}\mid l\in L\}$ ebenfalls eine starke Zusammenhangskomponente von G ist.

Anmerkung. Angenommen, der Implikationsgraph G von F enthält keine starke Zusammenhangskomponente, die ein Literal $l$ und dessen Negation ${\bar {l}}$ enthält. Sei G' der Graph, der durch Kontraktion der starken Zusammenhangskomponenten von G entsteht.¹⁾ Die folgende Prozedur konstruiert eine erfüllende Belegung τ von F:

Sei $K_{1},\dots ,K_{r}$ eine topologische Sortierung von $G'$. Wir betrachten die Komponenten $K_{i}$ der Reihe nach für $i=1,\dots ,r$ (insbesondere hat $K_{1}$ keine eingehenden Kanten). Sei σ i : var (K i ) → {0, 1} die Belegung, die jedem Literal $l\in K_{i}$ den Wert $\sigma _{i}(l)=0$ zuweist. Wir erweitern die Belegung τ um $\tau :=\tau \cup \tau _{i}$ wenn die Variablen in K i noch nicht belegt sind.

1. Gemeint ist der Graph $G'=(V',E')$ mit $V'=\{K\subseteq V\mid K{\text{ ist eine starke Zusammenhangskomponente von G}}\}$ und $E'=\{(K,K')\mid \exists v\in K,\exists v'\in K'{\text{ sodass }}(v,v')\in E\}$.

Aufgabe 5.4

Wenden Sie den Branch-and-Bound Algorithmus zum Finden eines minimalen Vertex Covers auf den nachfolgenden Graphen an. Geben Sie den Ablauf des Algorithmus als Branch-and-Bound-Baum wieder. Geben Sie für jeden Schritt die obere Schranke U' und die untere Schranke L' an, sowie die aktuelle Teilinstanz und die aktuell beste gefundene Lösung S. (Falls mehrere Knoten für einen Branching-Schritt in Frage kommen, wählen Sie den mit der kleinsten Nummer.)

Aufgabe 5.5

Sei G = (V, E) ein ungerichteter Graph. Ein Matching (in G) ist eine Teilmenge M ⊆ E von Kanten, sodass keine zwei Kanten aus M einen Knoten teilen. Das Maximum Matching Problem besteht darin, ein Matching mit größtmöglicher Kardinalität zu bestimmen. Beweisen Sie, dass Maximum Matching in Polynomialzeit gelöst werden kann, wenn der Eingabegraph ein Baum ist.

Hinweis: Orientieren Sie sich an dem in der Vorlesung besprochenen Algorithmus für Independent Set auf Bäumen.

Dieser Algorithmus ist größteils von den Folien und wurde nur minimal angepasst, damit er diese Aufgabe erfüllt.

m <- leere Menge an Kanten
    while T hat zumindest eine Kante
        Sei e = (u,v) eine Kante, sodass v ein Blatt ist
        Füge e zu m hinzu
        Lösche aus T die Knoten u und v, sowie alle zu diesen beiden Knoten inzidenten Kanten
return m

Aufgabe 5.6

Entwerfen und beschreiben Sie einen Branch-and-Bound-Algorithmus für das Optimierungsproblem Max 2Sat, welches wie folgt definiert ist:

Gegeben sei eine Menge von Boole’schen Variablen $V=\{x_{1},x_{2},\dots ,x_{n}\}$ sowie eine Menge $C=\{c_{1},c_{2},\dots ,c_{m}\}$ von Klauseln mit genau zwei Literalen, d.h. für jede Klausel $c_{i}\in C$ gilt $c_{i}=(l_{i}^{1}\lor l_{i}^{2})$ und $l_{i}^{k}=x$ oder $l_{i}^{k}=x$ für $k\in \{1,2\}$ und $x\in V$. Gesucht ist eine Wahrheitsbelegung der Variablen, die möglichst viele Klauseln erfüllt.

Beantworten Sie folgende Fragen:

(a) Wie repräsentieren Sie ein Teilproblem und wie erfolgt das Branching, d.h. das Aufteilen eines (Teil-)Problems in weitere Teilprobleme?

(b) Beschreiben Sie eine sinnvolle Möglichkeit für die Auswahl des nächsten Teilproblems. Nach welcher Strategie gehen Sie dabei vor?

(c) Geben Sie Heuristiken für die Berechnung einer unteren und oberen Schranke an.

Übung 6

Aufgabe 6.1

Betrachten Sie das Knotenfärbungsproblem OptColor für die wie folgt definierte Familie von Graphen $\{G_{i}\mid i\in N,i\geq 3\}$. Der Graph $G_{i}=(V_{i},E_{i})$ für $i\geq 3$ hat die Knotenmenge $V_{i}=\{x,v_{1},v_{2},\dots ,v_{i}\}$ und die Kantenmenge $E_{i}=\{(x,v_{j})\mid j=1,\dots ,i\}\cup \{(v_{j},v_{j+1})\mid j=1,\dots ,i-1\}\cup \{(v_{i},v_{1})\}$. Entwerfen Sie einen Algorithmus zur optimalen Färbung aller Graphen G i und geben Sie den zugehörigen Pseudocode an. Gehen Sie davon aus, dass der Pseudocode $V_{i}$ , $E_{i}$ und x zu dem Graphen $G_{i}$ als Übergabeparameter bekommt. Begründen Sie die Korrektheit und Optimalität der Färbung. Welche Beobachtungen können Sie über die optimalen Färbungen der Graphen $G_{i}$ machen?

Aufgabe 6.2

Das 4-Color Problem ist wie folgt definiert: Gegeben sei ein ungerichteter Graph G. Kann man die Knoten des Graphen mit den vier Farben A, B, C und D so einfärben, dass benachbarte Knoten nicht die gleiche Farbe besitzen?

Beweisen Sie, dass 4-Color NP-vollständig ist.

Hinweis: Sie können eine einfache Reduktion erstellen, indem Sie Ihr Wissen aus der Vorlesung nutzen, dass 3-Color NP-vollständig ist. Um zu beweisen, dass 4-Color in NP liegt, benutzen Sie die Definition von NP.

https://crypto.iti.kit.edu/fileadmin/User/TGI_WS13/Beispielreduktion.pdf

Aufgabe 6.3

Seien A, B, C, D Ja/Nein-Probleme in NP und n die Eingabegröße. Angenommen, es gibt

• eine Reduktion von A auf B mit Laufzeit O(n 2.5 ),
• eine Reduktion von B auf C mit Laufzeit O(n · log(n)),
• sowie eine Reduktion von C auf D mit Laufzeit O(n 4 ).

Beantworten Sie die folgenden Fragen:

1. Geben Sie die engste obere Schranke für die Laufzeit einer Reduktion von A auf D in O-Notation an, die sich aus diesen Annahmen ableiten lässt und begründen Sie die Antwort.
2. Nehmen Sie an, dass C NP-schwer ist. Was folgt daraus für die Komplexität der Probleme A, B, D?
3. Nehmen Sie an, D kann in Polynomialzeit gelöst werden. Was folgt daraus für die Komplexität der übrigen Probleme A, B, C?

Aufgabe 6.4

Lösen Sie die folgende Instanz des Gewichteten Interval Scheduling Pro- blems mittels Dynamischer Programmierung. Geben Sie das Array M an, sowie jeweils die Werte $w_{j}+M[p(j)]$ und M [j − 1]. Geben Sie außerdem für jeden Job j den Wert p(j) an. Berechnen Sie anschließend aus diesem Array eine Lösung und erklären Sie wie Sie zu dieser Lösung gekommen sind.

Job	Start	Ende	Gewicht
1	10	18	11
2	3	25	7
3	14	16	1
4	1	4	2
5	3	10	5
6	12	15	3
7	4	6	1
8	4	7	2
9	19	24	9
10	15	21	10
11	6	12	1

Aufgabe 6.5

Betrachten Sie folgenden rekursiven Algorithmus zur Berechnung des n-ten Elements einer Zahlenfolge.

Sequence(int n):
if n <= 4
    return 1
else
    return Sequence(n-Sequence(n - 1)) + Sequence(n-Sequence(n - 4))

Geben Sie die ersten 10 Elemente der Zahlenfolge an. Wandeln Sie dann den Algorithmus um in einen Algorithmus mittels Dynamischer Programmierung und analysieren Sie dessen Laufzeit. Was ist der größte Vorteil Ihres Dynamischen Programms gegenüber dem ursprünglichen Algorithmus?

Sequence(n):
erstelle S[] der Länge n
for i = 1 bis 4
    S[i] = 1
for i = 5 bis n
    S[i]= S[i - S[i-1]] + S[i - S[i-4]]
return S[n]

Die Laufzeit liegt in O(n). Berechnete Zwischenergebnisse werden abgespeichert und müssen somit nicht neu berechnet werden.

Aufgabe 6.6

Gegeben sei eine Folge $(a_{i})_{0\leq 1\leq n}$ von n natürlichen Zahlen. Ihre Aufgabe ist es, die Länge der längsten strikt aufsteigenden Teilfolge in (a i ) zu bestimmen, in der keine zwei geraden Zahlen aufeinanderfolgen dürfen. Entwerfen und beschreiben Sie einen Algorithmus mittels Dynamischer Programmierung um dieses Problem zu lösen. Die Laufzeit soll $O(n^{2})$ nicht überschreiten.

Beispiel: Sei $(a_{i})=(9,2,1,4,5,6,10,7,8)$. Die Folge (1, 4, 5, 7, 8) als Teilfolge von $(a_{i})$ wäre zulässig, da die Folge strikt aufsteigend ist und keine zwei aufeinanderfolgenden Zahlen gerade sind. Die Folge (1, 4, 6, 7, 8) ist nicht zulässig, da sie zwei aufeinanderfolgende Zahlen enthält, die gerade sind. Die längste Teilfolge von (a i ), die strikt aufsteigend ist und keine zwei aufeinanderfolgenden Zahlen enthält, die gerade sind, ist in diesem Beispiel (1, 4, 5, 6, 7, 8).

Func(seq[]):
in = neues Array der Länge seq.length
max = 0
for i = 0 bis seq.length - 1
    for j = 0 bis i - 1
        if seq[j] < seq[i] und !(seq[i]%2==0 && seq[j]%2==0) und in[j] > in[i]
            in[i] = in[j]
    in[i] = in[i] + 1
    max = max(in[i], max)
return max

Übung 7

Aufgabe 7.1

Betrachten Sie die folgende Instanz des symmetrischen Traveling Salesman Problems:

Wenden Sie die Spanning-Tree-Heuristik aus der Vorlesung auf diese Instanz an und illustrieren Sie klar jeden Ihrer Schritte. Konstruieren Sie dabei Ihre Eulertour von A ausgehend und besuchen Sie die möglichen Knoten in alphabetischer Reihenfolge, wenn diese nicht eindeutig ist. Welche Länge hat Ihre Tour P ? Ist hier die Gütegarantie 2 aus der Vorlesung eingehalten?

Aufgabe 7.2

Gegeben ist eine Instanz I = (G, k) von Independent Set mit dem unten abgebildeten Eingabegraph G. Wenden Sie der Reihe nach die in der Vorlesung besprochenen Problemreduktionen von Independent Set auf Vertex Cover sowie von Vertex Cover auf Set Cover an, um aus der Instanz I eine äquivalente Instanz I' = (S', k') von Set Cover zu erzeugen.

Aufgabe 7.3

Eine einfache Heuristik für das Traveling Salesman Problem (TSP) ist die Nearest Neighbor Heuristik. Sie startet bei einem beliebigen Knoten und gehen dann immer zu einem noch nicht besuchten nächstliegenden Knoten weiter. Sind alle Knoten erreicht, wird der Pfad zu einer Rundtour geschlossen.

Zeigen Sie mit einem möglichst einfachen Beispiel, dass diese Heuristik auch für das Euklidische TSP nicht immer eine optimale Lösung liefert.

Weiters: Beweisen oder widerlegen Sie, dass diese Heuristik für das Euklidische TSP die Gütegarantie 3/2 besitzt.

Aufgabe 7.4

Gegeben ist eine Variante des Rucksack-Problems, bei der jeder Gegenstand beliebig oft gewählt werden kann. Zeigen Sie, dass der Greedy-Algorithmus aus der Vorlesung für dieses Problem eine Gütegarantie von 1/2 erzielt.

Aufgabe 7.5

Sei G = (V, E) ein gerichteter Graph. Jeder Kante (u, v) ∈ E ist ein Symbol σ(u, v) aus einem endlichen Alphabet Σ zugeordnet (es kann auch mehrere ausgehende Kanten mit dem gleichen Symbol geben), sodass jede Kantenfolge ein Wort aus Σ ∗ erzeugt. Umgekehrt muss ein Wort $s=(\tau _{1},\dots ,\tau _{k})$ nicht unbedingt einer Kantenfolge in G entsprechen.

(a) Geben Sie einen Polynomialzeitalgorithmus an, der für einen Eingabegraphen G, einen Startknoten v 0 , und ein Wort s entscheidet, ob eine von v 0 ausgehende Kan- tenfolge in G existiert, die das Wort s erzeugt, und gegebenenfalls eine entspechende Kantenfolge zurückliefert.

Angenommen, jeder Kante (u, v) ∈ G ist eine Wahrscheinlichkeit p(u, v) > 0 zugeordnet, mit der die Kante ausgehend von u gewählt wird. Für jeden Knoten u ergibt die Summe der Wahrscheinlichkeiten der von u ausgehenden Kanten 1. Sei $\pi =(e_{1},\dots ,e_{k})$ eine von Knoten v ausgehende Kantenfolge. Das Produkt $p(\pi )=\prod _{i=1}^{k}p(e_{i})$ entspricht der Wahrscheinlichkeit, dass ein von v ausgehender "Random Walk", bei dem an jedem Knoten u zufällig eine ausgehende Kante (u, w) mit Wahrscheinlichkeit p(u, w) gewählt wird, die Kantenfolge π wählt.

(b) Erweitern Sie Ihren Algorithmus aus Unteraufgabe (a), sodass er eine wahrschein- lichste von v 0 ausgehende Kantenfolge zurückliefert, die das Wort s erzeugt. Welche (asymptotische) Laufzeit hat Ihr Algorithmus, in Abhängigkeit von |V |, |E| und |s|?

Aufgabe 7.6

Gegeben ist das folgende Planungsproblem. Ein Roboter bewegt sich auf einem Raster $S=\{1,\dots ,n\}\times \{1,\dots ,n\}$ mit $n\times n$ Feldern. Zu jedem Zeitpunkt $t\in \{0,\dots ,T\}$ kann er an seinem aktuellen Standort $S_{t}\in {\mathcal {S}}$ eine der vier Richtungen $A_{t}\in \{{\text{oben, unten, links, rechts}}\}$ wählen. Er bewegt sich daraufhin auf das in dieser Richtung gelegene benachbarte Feld $S_{t+1}$ und erhält einen dem Feld $S_{t+1}$ zugeordneten Wert ${\mathcal {R}}(S_{t+1})\in \mathbb {Q}$ als Belohnung $R_{t+1}$ , es sei denn, er würde das Raster dadurch verlassen—in diesem Fall bewegt er sich nicht von der Stelle und erhält eine "Belohnung" von $R_{t+1}=-1$.

Eine Strategie ist eine Funktion

$\pi :{\mathcal {S}}\times {0,\dots ,T-1}\rightarrow \{{\text{oben, unten, links, rechts}}\}$,

die für jeden Standort und Zeitpunkt die Bewegungsrichtung des Roboters angibt. Für jeden Startpunkt S 0 ∈ S und jede Strategie π ergibt sich eine Episode

$S_{0},A_{0},R_{1},S_{1},A_{1},R_{2},S_{2},\dots ,S_{t-1},A_{t-1},R_{T}$.

Der Nutzen G t für einen Zeitpunkt t ist die P Summe aller Belohungen, die der Roboter bis zum Ende der Episode erhält, also ${\textstyle G_{t}=\sum _{i=t+1}^{T}R_{i}}$. Eine optimale Strategie ist eine Strategie $\pi ^{*}$, die für jeden Standort $S_{t}$ ab dem Zeitpunkt t den maximalen Nutzen $G_{t}$ liefert. Der Wert $v^{*}(S,t)$ eines Punktes $S\in {\mathcal {S}}$ zum Zeitpunkt $t\in \{0,\dots ,T-1\}$ entspricht dem von einer optimalen Strategie $\pi ^{*}$ erzielten Nutzen G t bei Startpunkt $S_{t}=S$.

Geben Sie einen Polynomialzeitalgorithmus an, der die Dimension n des Rasters, die Länge T einer Episode, sowie die Funktion ${\mathcal {R}}:{\mathcal {S}}\rightarrow \mathbb {Q}$ (als Tabelle) als Eingaben erhält, und für jeden Punkt S ∈ S mittels dynamischer Programmierung den Wert $v^{*}(S,0)$ berechnet. Nutzen Sie dazu Bellmans Gleichungen.

Wenden Sie Ihren Algorithmus auf die unten dargestellte Instanz mit n = 4 und T = 3 an (der Wert ${\mathcal {R}}(i,j)$ ist in Abbildung 1 im jeweiligen Feld eingetragen). Stellen Sie die von einer optimalen Strategie $\pi ^{*}(S,t)$ vorgeschlagenen Bewegungsrichtungen für t = 0 dar, indem Sie Abbildung 2 vervollständigen.

Abbildung 1: ${\mathcal {R}}(i,j)$

0	0	0	8
0	0	0	0
0	10	0	0
0	5	0	0

Abbildung 2: (Eine) optimale Strategie $\pi ^{*}$ für t=0.

		←

Materialien

Neues Material hinzufügen

T

• Task21.png (details)
• Task22 solution.png (details)
• Task22.png (details)
• Task27.png (details)
• Task31.png (details)
• Task34 solution.jpg (details)
• Task36.png (details)
• Task52 solution.jpeg (details)
• Task52.png (details)
• Task53.png (details)
• Task54.png (details)
• Task71.png (details)
• Task72.png (details)