TU Wien:Algorithmen und Datenstrukturen VU (Szeider)/Test 1 2018S
26. April 2018 Gruppe A
Sie dürfen die Lösungen nur auf die Angabeblätter schreiben, die Sie von der Aufsicht erhalten. Es ist nicht zulässig, eventuell mitgebrachtes eigenes Papier zu verwenden. Benutzen Sie bitte dokumentenechte Schreibgeräte (keine Bleistifte!). Die Verwendung von Taschenrechnern, Mobiltelefonen, Tablets, Digitalkameras, Skripten, Büchern, Mitschriften, Ausarbeitungen oder vergleichbaren Hilfsmitteln ist unzulässig.
Kennzeichnen Sie bei Ankreuzfragen eindeutig, welche Kästchen Sie kreuzen!
Algorithmenanalyse[Bearbeiten | Quelltext bearbeiten]
a) (3 Punkte) Geben Sie für das Codestück FunktionA die Laufzeit in Abhängigkeit von n in Θ-Notation an.
FunktionA(n):
Input: n ≥ 1
z←0
for j ← 1, . . . , n
z ←z+j+1
k←0
while k ≤ n
k ←k+j
while z > 0
z ← ⌊z/2⌋
Laufzeit: Θ( )
Hinweis: Es gilt .
b) (3 Punkte) Geben Sie für das Codestück FunktionB den Rückgabewert (z) in Abhängigkeit von n in Θ-Notation an.
FunktionB(n):
Input: n ≥ 1
i←1
a←1
repeat
i=i+1
a=a·2
until i ≥ log2 n
z←0
for j ← 0, . . . , a
z ←z+j+n
return z
Rückgabewert (z): Θ( )
c) (4 Punkte) (i) Vervollständigen Sie die folgende Definition:
- Eine Funktion T (n) ist in O(f (n)) wenn
(ii) Gegeben ist die folgende Funktion:
Sind die nachfolgenden Abschätzungen wahr, wenn man die gegebenen Werte
für n0 und c in der jeweiligen Definition der asymptotischen Notation einsetzt?
Kreuzen Sie die zutreffende Antwort an.
n0 c Richtig Falsch
g ist in O(n2 ) 10 3
g ist in O(n3 ) 4 1
g ist in Ω(1) 6 100
(richtiges Kreuz +1 Punkt; falsches Kreuz -1 Punkt; kein Kreuz 0 Punkte; negative Summe wird auf 0 gesetzt)
Greedy-Algorithmen[Bearbeiten | Quelltext bearbeiten]
a) (6 Punkte) Im Folgenden definieren wir ein Scheduling Problem. Gegeben ist eine
Menge von Jobs J = {1, . . . , n}, die alle abgearbeitet werden müssen. Für jeden
Job, j ∈ J, ist eine Bearbeitungsdauer pj > 0, und ein Gewicht wj > 0 spezifiziert.
Wie beim Interval Scheduling, können Jobs nicht unterbrochen werden und es kann
immer nur ein Job zu einem Zeitpunkt ausgeführt werden.
Ziel ist es, allen Jobs, jP∈ J, eine Startzeit sj zuzuweisen, sodass die Summe der
gewichteten Endzeiten j∈J wj fj minimal ist, wobei die Endzeit eines Jobs, j ∈ J,
durch fj = sj + pj gegeben ist.
Ein Algorithmus führt die Jobs unmittelbar aufeinanderfolgend aus. Zur Bestim-
mung der Reihenfolge sind zwei Strategien gegeben. Beurteilen Sie, ob das jeweilige
Kriterium immer zu einer optimalen Lösung führt. Geben Sie ein Gegenbeispiel
an, wenn Optimalität nicht garantiert ist.
(i) Ordne die Prozesse aufsteigend gemäß ihrer Bearbeitungsdauer.
Optimal: Ja Nein
Gegenbeispiel:
(ii) Ordne die Prozesse absteigend gemäß ihres Gewichtes.
Optimal: Ja Nein
Gegenbeispiel:
Hinweis: Spezifizieren Sie ggf. möglichst kleine Gegenspiele in Form konkreter Mengen von Paaren: {(p1 , w1 ), (p2 , w2 ), . . . }. Eine Begründung ist nicht erforderlich.
b) (2 Punkte) Betrachten Sie die folgenden Behauptungen in Bezug auf minimale
Spannbäume für schlichte ungerichtete zusammenhängende Graphen und kreuzen Sie die korrekten an.
Der minimale Spannbaum eines Graphen enthält zumindest eine Kante mi- nimalen Gewichtes innerhalb jeder Kantenschnittmenge. Das Kreislemma besagt, dass die günstigste Kante jedes in einem Graph ent- haltenen Kreises Teil des minimalen Spannbaumes dieses Graphen sein muss. Der Algorithmus von Prim und der Algorithmus von Kruskal berechnen gülti- ge minimale Spannbäume und retournieren somit zwangsläufig denselben Spannbaum. Der Algorithmus von Kruskal ist wegen seiner Laufzeitkomplexität auf dünnen Graphen gegenüber dem Algorithmus von Prim zu bevorzugen.
(2 Punkte, wenn alle Kreuze korrekt sind, 1 Punkt bei genau einem Fehler, ansonsten 0 Punkte)
Dijkstra und Heap[Bearbeiten | Quelltext bearbeiten]
Gegeben ist die folgende Beschreibung einer Ausführung des Algorithmus von Dijkstra zum Finden eines kürzesten Pfades auf einem gerichteten Graphen in der Implementierung mit einer Liste.
1. Discovered = ∅, L = {s, v1 , v2 , v3 , v4 , u}
Vertex s v1 v2 v3 v4 u
d(·) 0 ∞ ∞ ∞ ∞ ∞
2. Discovered = {s}, L = {v1 , v2 , v3 , v4 , u}
Vertex s v1 v2 v3 v4 u
d(·) 0 ∞ 5 ∞ 3 ∞
3. Discovered = {s, v4 }, L = {v1 , v2 , v3 , u}
Vertex s v1 v2 v3 v4 u
d(·) 0 ∞ 4 ∞ 3 ∞
4. Discovered = {s, v4 , v2 }, L = {v1 , v3 , u}
Vertex s v1 v2 v3 v4 u
d(·) 0 12 4 5 3 ∞
5. Discovered = {s, v4 , v2 , v3 }, L = {v1 , u}
Vertex s v1 v2 v3 v4 u
d(·) 0 9 4 5 3 15
6. Discovered = {s, v4 , v2 , v3 , v1 }, L = {u}
Vertex s v1 v2 v3 v4 u
d(·) 0 9 4 5 3 12
7. Discovered = {s, v4 , v2 , v3 , v4 , u}, L = ∅
Vertex s v1 v2 v3 v4 u
d(·) 0 9 4 5 3 12
a) (2 Punkte) Extrahieren Sie aus diesem Ablauf den kürzesten Pfad von s nach u
sowie seine Länge. (Geben Sie den Pfad als Liste von Knoten an).
Pfad:
Länge:
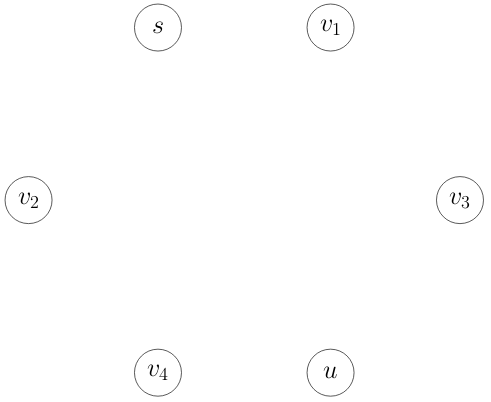
b) (4 Punkte) Zeichnen Sie die Kanten und Kantengewichte eines minimalen (so we-
nige Kanten wie möglich) Graphen, der zu einem solchen Ablauf führt, in der folgenden Grafik ein.
c) (2 Punkte) Geben Sie für die folgenden Operationen an, ob sie im Worst-Case asymptotisch in Bezug auf die Anzahl der Elemente schneller in einem Min-Heap, in einem sortierten Array oder in beiden gleich schnell ausgeführt werden können.
(i) Finden des minimalen Elements:
- Min-Heap / sortiertes Array / asymptotisch gleich schnell
(ii) Einfügen eines beliebigen Elements:
- Min-Heap / sortiertes Array / asymptotisch gleich schnell
(iii) Erstellen aus einem unsortierten Array:
- Min-Heap / sortiertes Array / asymptotisch gleich schnell
(iv) Finden des maximalen Elements:
- Min-Heap / sortiertes Array / asymptotisch gleich schnell
(2 Punkte, wenn alle Kreuze korrekt sind, 1 Punkt bei genau einem Fehler, ansonsten 0 Punkte)
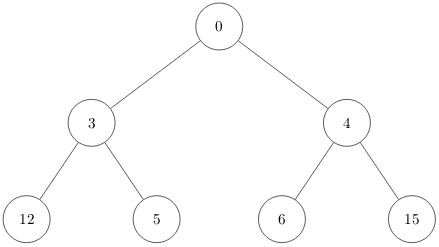
d) (4 Punkte) Gegeben ist der folgende Min-Heap H:
Hinweis: Gehen Sie bei den Teilaufgaben (i) und (ii) jeweils von diesem Heap aus.
(i) Zeichnen Sie den Heap H, wie er nach dem Einfügen des Element 1 aussieht.
(ii) Zeichnen Sie den Heap H, wie er nach dem Löschen des Element 0 aussieht.
Divide-and-Conquer[Bearbeiten | Quelltext bearbeiten]
a) (6 Punkte) Führen Sie den Quicksort-Algorithmus auf folgendes Array (Index star-
tet bei 0) aus, um es aufsteigend zu sortieren:
[ 18, 1, 22, 34, 6, 27, 2, 4 ]
Als Pivotelement wird jeweils das Element an der Position ⌊n/2⌋ gewählt. Geben Sie die Zwischenschritte nach jedem Aufteilen an und markieren Sie jeweils das als nächstes gewählte Pivotelement. Der Schritt des Aufteilens ist so implementiert, dass die Elemente einer Subfolge immer in der gleichen Reihenfolge angeordnet werden wie in der Originalfolge.
b) (4 Punkte) Geben Sie ein Eingabearray mit 8 unterschiedlichen Elementen an,
sodass der Quicksort-Algorithmus aus Teilaufgabe a) Worst-Case-Laufzeit hat.
Graphen[Bearbeiten | Quelltext bearbeiten]
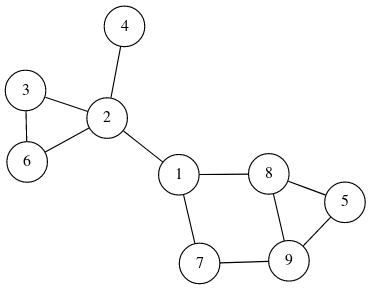
Sei G der folgende ungerichtete schlichte zusammenhängende Graph mit Knoten V und Kanten E:
Macht das Entfernen einer Kante b ∈ E den Graphen unzusammenhängend, so nennen wir b eine Brücke.
a) (2 Punkte) Markieren Sie im oben abgebildeten Graphen alle Brücken.
b) (2 Punkte) Wir führen nun im Graphen eine Tiefensuche durch. Aus der Entde-
ckungsreihenfolge der Knoten entsteht ein Baum. Eine Kante v → w in diesem
Baum drückt aus, dass w von v aus entdeckt wurde. Wir bezeichnen v als El-
ternknoten von w.
Wird bei der Tiefensuche durch eine Kante r ein bereits entdeckter Knoten ge-
ringerer Tiefe gefunden, der nicht der Elternknoten ist, so nennen wir r eine
Rückwärtskante. Das heißt, sie beginnt unten und zeigt auf einen Knoten weiter
oben im Baum.
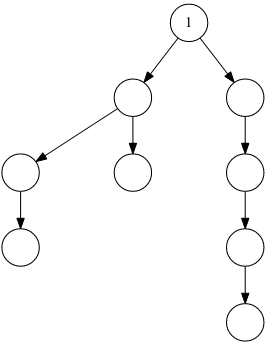
Vervollständigen Sie den unten dargestellten Tiefensuchbaum für den oben abge-
bildeten Graphen. Lässt die Suche eine Auswahl zwischen Knoten zu, wählen Sie
den numerisch kleinsten. Ergänzen Sie dabei die Rückwärtskanten.
c) (6 Punkte) Es gilt nun einen effizienten Algorithmus zur Bestimmung aller Brücken eines beliebigen ungerichteten schlichten zusammenhängenden Graphen zu finden.
Kreuzen Sie im folgenden Pseudocode die Codezeilen an, die ausgeführt werden müssen, um die Brücken zu finden. Je Block ist genau eine Zeile richtig.
Hinweis: Teilaufgabe b) gibt bereits einen guten Hinweis auf die Idee des gesuchten Algorithmus. Betrachten Sie dabei die Rückwärtskanten und Brücken im Baum.
(richtiges Kreuz +2 Punkte; falsches Kreuz/mehrere Kreuze im Block -2 Punkte; kein Kreuz 0 Punkte; negative Summe wird auf 0 gesetzt)
// Mengen R und B, sowie Arrays Tiefe und Eltern sind global.
Brücken(Graph G, Startknoten s):
R←∅ // Rückwärtskanten
B←∅ // Baumkanten
foreach v ∈ V do
Tiefe[v] ← −1
Eltern[v] ← null
call Tiefensuche(G, s, 0)
foreach (v, w) ∈ R do
foreach (v, w) ∈ B do
foreach (v, w) ∈ E do
while v 6= w
x ← Eltern[v]
B ← B ∪ {(x, v)}
B ← B ∩ {(x, v)}
B ← B \ {(x, v)}
v←x
return B
Tiefensuche(Graph G, Knoten v, Tiefe d):
Tiefe[v] ← d
// für jeden an v adjazente Knoten w
foreach (v, w) ∈ E do
if Tiefe[w] = −1 then
Eltern[w] ← v
B ← B ∪ {(v, w)}
call Tiefensuche(G, w, d + 1)
else if (Eltern[v] 6= w) and (d > Tiefe[w]) then
R ← R ∪ {(v, w)}
R ← R ∪ {(w, Eltern[v])}
R ← R ∪ {(v, Eltern[w])}