TU Wien:Algorithmen und Datenstrukturen VU (Szeider)/Zusammenfassung Test 2

Der Stoff vom 1. Test kommt auch.

Komplexitätstheorie

Video vom MIT

Arten von Problemen:

Entscheidungsproblem

Hat eine Ja oder Nein Antwort.

Funktionales Problem

Hat eine Antwort komplexer als Ja/Nein.

Optimierungsproblem

Gesucht ist die beste Lösung.

Polynomialzeitreduktion

Wir beschränken uns auf Entscheidungsprobleme.

$A\leq _{P}B$ ... Polynomialzeitreduktion von Problem A auf Problem B

Polynomialzeitalgorithmus der Eingaben von A zu Eingaben von B, welche die gleiche Antwort liefern, konvertiert.

• Lösung durch Reduktion
• Nicht-Handhabbarkeit zeigen

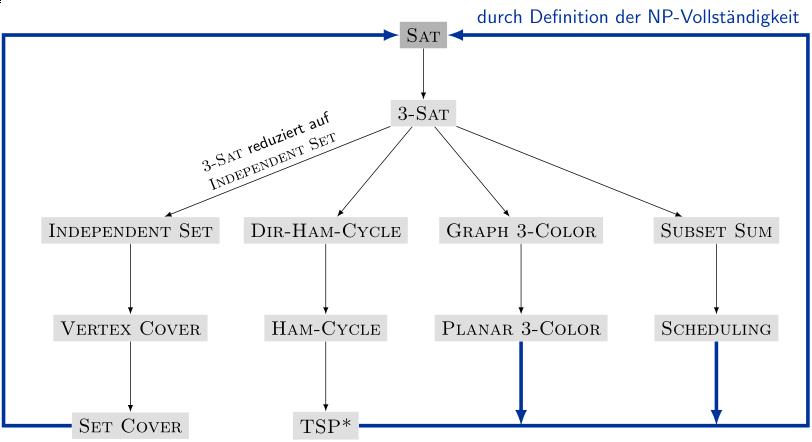
Reduktionsstrategien

• Einfache Äquivalenz
  Vertex Cover $\equiv _{P}$ Independent Set [1]
• Spezieller Fall auf allgemeinen Fall
  Vertex Cover $\leq _{P}$ Set Cover
• Kodierung mit Gadgets
  3-Sat $\leq _{P}$ Independent Set

Transitivität

$X\leq _{P}Y\land Y\leq _{P}Z\supset X\leq _{P}Z$

Erfüllbarkeit

Literal: Eine boolesche Variable oder ihre Negation: $x_{i}$ oder ${\overline {x_{i}}}$

Klausel: Eine Disjunktion von Literalen

Erfüllbarkeitsproblem (Sat, von satisfiability)

3-Sat

SAT, bei dem jede Klausel genau 3 Literale enthält.

3-Sat $\leq _{P}$ Independent Set

Komplexitätsklassen

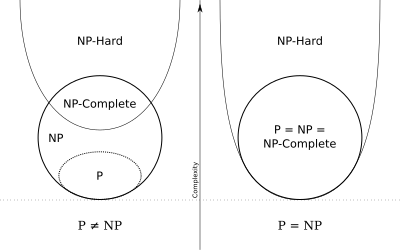
P

Enthält alle Entscheidungsprobleme, die in Polynomialzeit für deterministische Turingmaschinen lösbar sind.

NP

Enthält alle Entscheidungsprobleme, bei denen es für Ja-Antworten Beweise gibt, die in Polynomialzeit verifiziert werden können.

NP-schwer

Ein Entscheidungsproblem, wenn alle Probleme in NP auf es in Polynomialzeit reduziert werden können.

NP-vollständig

Ein Entscheidungsproblem, wenn es in NP liegt und NP-schwer ist.

NP-Probleme

NP = nicht-deterministisch polynomielle Zeit

Zertifikat

Ein Zertifikat $t$ für einen Input $x$ ist ein beliebiger String dessen Länge polynomiel in der Länge von $x$ beschränkt ist, das heißt $|t|\leq p(|x|)$ gilt für ein Polynom $p$.

Zertifizierer

Einen Polynomialzeitalgorithmus $C(x,t)$, der Ja-Instanzen $x$ mit Hilfe von Zertifikaten $t$ überprüft, nennt man Zertifizierer.

Siehe auch Karp's 21 NP-complete problems.

Independent Set

Knotenteilmenge, in der keine zwei Knoten adjazent sind. Gibt es Independent Set S, sodass |S| ≥ k?

Vertex Cover

Knotenteilmenge, sodass jede Kante mit min. einem der Knoten inzidiert. Gibt es ein Vertex Cover S, sodass |S| ≤ k?

Set Cover

Gegeben ist eine Menge S von Teilmengen von Elementen in einem Universum. Ein Set Cover ist eine Teilmenge von S, deren Vereinigung dem Universum entspricht. Gibt es ein Set Cover C, sodass |C| ≤ k?

Hamiltonkreis

Existiert ein Kreis C, der alle Knoten genau einmal enthält?

Travelling Salesman Problem (TSP)

Gesucht ist die Reihenfolge für die Besuche mehrer Knoten, in einem kantengewichtetem Graphen. Der erste Knoten sollte gleich dem letzten Knoten sein. Gibt es eine Tour T, sodass |T| ≤ k?

Knotenfärbung

Erlaubt der Graph eine Färbung mit k Farben, sodass keine zwei benachbarten Knoten dieselbe Farbe haben?

Rucksackproblem

Gegeben sind Gegenstände mit Gewichten und Werten, und eine Kapazität G (alles positiv rational). Gesucht ist eine Teilmenge der Gegenstände mit Gesamtgewicht ≤ G und maximalem Gesamtwert.

NP-Vollständigkeit Spezialfälle

• Finden von kleinen Vertex Covers
• Independent Set auf Bäumen
• Gewichtetes Independent Set auf Bäumen
  • ${\textstyle OPT_{\text{in}}(u)=w_{u}+\sum _{v\in {\text{Nachfolger}}(u)}OPT_{\text{out}}(v)}$
  • ${\textstyle OPT_{\text{out}}(u)=\sum _{v\in {\text{Nachfolger}}(u)}\max\{OPT_{\text{in}}(v),OPT_{\text{out}}(v)\}}$
• Knotenfärben in Intervallgraphen

Optimierung

Kombinatorische Optimierung

Es geht bei der kombinatorischen Optimierung darum, aus einer (großen) Menge von diskreten Elementen eine Teilmenge zu konstruieren, die gewissen Nebenbedingungen entspricht und bezüglich einer Kostenfunktion optimal ist.

Branch-and-Bound

Wikipedia

Beschränke eine auf Divide-and-Conquer basierende systematische Durchmusterung aller Lösungen mit Hilfe von Methoden, die untere und obere Schranken liefern, und ermittle eine optimale Lösung.

Rucksackproblem

Verbesserung der Enumeration

• Untere Schranke: Greedy-Algorithmus
• verbesserte obere Schranke: wenn ein Gegenstand nicht passt wird er teilweise eingepackt

Maximierungsproblem

Bounding: Für jedes Teilproblem wird

• eine lokale obere Schranke U' (upper bound) und
• eine lokale untere Schranke L' (lower bound) berechnet

Abbruch wenn $U'\leq L$

Minimales Vertex Cover

Matching

Kantenmenge, wenn keine zwei Kanten einen Knoten gemeinsam haben.

Untere Schranke L'

Größe eines nicht erweiterbaren Matchings

Wähle beliebige Kante (u,v), entferne u und v samt inzidenten Kanten, solange bis keine Kante mehr vorhanden ist. Anzahl der gewählten Kanten entspricht Größe des Matchings.

Obere Schranke U'

$S\leftarrow \emptyset$. Solange der Graph Kanten enthält:

1. Sortiere die Knoten nach absteigendem Knotengrad.
2. Füge den Knoten u mit höchstem Knotengrad zu S hinzu.
3. Entferne u und alle seine inzidenten Kanten.

obere Schranke = |C'|+|S|

Dynamische Programmierung

Teile das Problem in eine Folge von überlappenden Teilproblemen auf und erstelle und speichere Lösungen für immer größere Teilprobleme unter Verwendung der abgespeicherten Lösungen.

Optimalitätsprinzip von Bellman

Dynamische Programmierung führt genau dann zu einem optimalen Ergebnis, wenn es sich aus den optimalen Ergebnissen der Subprobleme zusammensetzt.

Gewichtetes Interval Scheduling

Ziel: Finde eine Teilmenge maximalen Gewichts von paarweise kompatiblen Jobs.

Compute-Opt(j):
if j = 0
  return 0
else
  return max(wj + Compute-Opt(p(j)), Compute-Opt(j − 1))

Segmented Least Squares

Gegeben seien n Punkte in der Ebene. Gesucht ist eine Gerade $y=ax+b$, welche die Summe des quadrierten Fehlers minimiert.

${\text{Err}}=\sum _{i=1}^{n}(y_{i}-(ax_{i}+b))^{2}$

Kürzeste Pfade

Bellman-Ford-Algorithmus

Shortest-Path(G,s,t):
foreach node v ∈ V
    M[0,v] ← ∞
M[0,t] ← 0
for i ← 1 bis |V| − 1
    foreach Knoten v ∈ V
        M[i,v] ← M[i − 1,v]
    foreach Kante (v,w) ∈ E
        M[i,v] ← min(M[i,v],cvw + M[i − 1,w])
return M[n − 1, s]

Push-Based-Shortest-Path(G,s,t):
foreach Knoten v ∈ V
    M[v] ← ∞
    Nachfolger[v] ← ∅
M[t] = 0
for i ← 1 bis |V| − 1
    foreach Kante (v, w) ∈ E
         if M[v] > M[w] + cvw
             M[v] ← M[w] + cvw
             Nachfolger[v] ← w
    if kein M[w] Wert andert sich in Iteration i, stop.
return M[s]

Approximation

Wikipedia

Die Güte eines Approximationsalgorithmus A für die Eingabe x sei definiert als:

${\frac {c_{\text{A}}(x)}{c_{\text{opt}}(x)}}:={\frac {\text{Lösung des Algorithmus}}{\text{optimale Lösung}}}$

Garantiert ein Algorithmus eine Güte ≤ ε für Minimierungsprobleme bzw. ≥ ε für Maximierungsprobleme, so heißt der Wert ε Gütegarantie und man spricht von einem ε-Approximationsalgorithmus.

Es folgt:

• für Minimierungsprobleme: ε ≥ 1,
• für Maximierungsprobleme: 0 ≤ ε ≤ 1
• ε = 1 ⇔ der Algorithmus ist exakt

2-Approximationsalgorithmus für Vertex Cover

Approx-Vertex-Cover(G):
C ← ∅
while E != ∅
    Wähle eine beliebige Kante (u, v) ∈ E
    C ← C ∪ {u, v}
    Entferne aus E alle Kanten, die inzident zu u oder v sind
return C

Spanning-Tree-Heuristik (ST) für das symmetrische TSP

symmetrisches TSP: Für alle Knotenpaare sind die Kantenlängen in beide Richtungen identisch.

Aus Wikipedia:

1. minimaler Spannbaum
2. verdopple jede Kante
3. Wähle einen beliebigen Startknoten und folge den Kanten des verdoppelten Spannbaums im Sinne eines Eulerkreises. Bereits besuchte Knoten werden dabei durch die direkte Kante zum folgenden Knoten übersprungen, sofern es sich nicht um den letzten Knoten des Kreises handelt.

Der Algorithmus von Hierholzer findet einen Eulerkreis (falls vorhanden) in einem Graphen G in linearer Zeit.

Lastverteilung

m identische Maschinen, n Jobs, Job j hat die Bearbeitungszeit t_j.

• Jeder Job j muss ununterbrochen auf einer Maschine ausgeführt werden.
• Eine Maschine kann nur einen Job auf einmal ausführen.

Center Selection

Gegeben ist eine Menge von n Standorten und eine ganze Zahl k > 0.

Wähle k Mittelpunkte C, so dass die maximale Distanz von einem Standort zu einem nächsten Mittelpunkt minimiert wird.

Heuristische Verfahren

Erzeuge in polynomieller Zeit eine Näherungslösung. In der Praxis kann eine solche Lösung häufig sehr gut oder sogar optimal sein, es gibt aber keine Garantie dafür.

Lokale Suche

Idee: Versuche eine Ausgangslösung durch kleine Änderungen iterativ zu verbessern

wichtige Komponenten:

• Lösungsrepräsentation
• Nachbarschaftsstruktur
• Schrittfunktion (best improvement, next improvement, random neighbor)
• Abbruchkriterium

Maximaler Schnitt (MAX-CUT)

Gegeben sei ein ungerichteter Graph G = (V, E) mit positiven ganzzahligen Kantengewichten $w_{uv}$ für alle Kanten (u, v) ∈ E. Finde eine Partition der Knoten (A, B), sodass das Gesamtgewicht von Kanten, die Knoten in den unterschiedlichen Partitionen verbinden, maximiert wird.

Metaheuristiken

Sind problemunabhängig formulierte Algorithmen zur heuristischen Lösung schwieriger Optimierungsaufgaben.

Simulated Annealing

Metropolis Kriterium

Tabu-Suche (TS)

• Vermeidung von Zyklen durch Verbieten des Wiederbesuchens früherer Lösungen.
• Best Improvement Schrittfunktion
• Tabulistenlänge ist kritisch
  • zu kurz → Zyklen, zu lang → verbietet viele mögliche Lösungen
  • geeignete Länge meist problemspezifisch, muss experimentell bestimmt, zufällig gewählt, oder adaptiv angepasst werden (Reactive Tabu Search)
• Aspirationskriterium: überschreibt den Tabu-Status einer "interessanten" Lösung

Evolutionäre Algorithmen

• Population: Es wird mit einer Menge von aktuellen Kandidatenlösungen gearbeitet.
• Selektion
• Rekombination
• Mutation

Materialien

Neues Material hinzufügen

N

• Np-complete-reductions.png (details)

P

• P np np-complete np-hard.svg (details)