TU Wien:Analysis VU (diverse)/Übungen 2024S/Beispiel 362
Bestimmen Sie alle Tangenten mit Anstieg an die Kurve .
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
Theoretische Grundlagen[Bearbeiten | Quelltext bearbeiten]
Hauptsatz über implizite Funktionen[Bearbeiten | Quelltext bearbeiten]
offene Menge, stetig differenzierbare Funktion,
Dann gibt es in der Umgebung eine eindeutig bestimmbare und stetig differenzierbare Lösung y(x) und es gilt:
Lösungsvorschlag von Matmö[Bearbeiten | Quelltext bearbeiten]
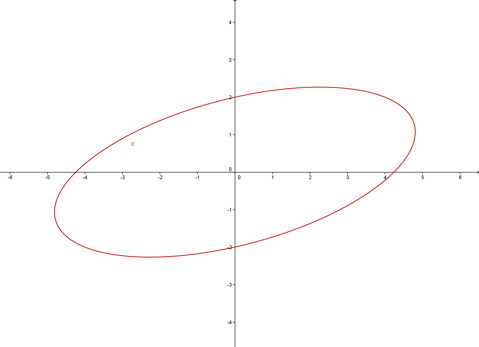
Wenn wir uns die Funktion ausgeben lassen, dann sieht das so aus:
Wir haben es also mit einer Ellipse zu tun. Wenn man da versucht "normal" abzuleiten kommt man relativ schnell zu dem Schluss, das da alles Mögliche rauskommt, nur nicht die Tangente, die man sucht: schlecht.
Zu unserem Glück hat sich aber ein(e) sehr gscheite(r) Mathematiker(in) den Hauptsatz über implizite Funktionen einfallen lassen (Der Legende nach füllt alleine der Beweis dieses Satzes mehrere Din-A4-Seiten). Uns soll das jetzt aber alles nicht kümmern, sondern wir schauen lieber mal, ob er irgendetwas zur Lösung unseres Problems beitragen kann:
Da wir die Tangenten mit dem Anstieg suchen, setzen wir die Funktion erst mal auf 1:
Mit ein bisschen Umformen kommt man dann auf
Dann wollen wir diese Erkenntnis mal in die ursprüngliche Funktion einsetzen:
Wenn wir x nun explizit machen und die Wurzel ziehen, kommen wir auf folgende Lösung: . Somit haben wir auch schon die zwei Punkte bestimmt, an denen die Steigung der Tangente 1 beträgt:
Jetzt müssen wir aus den Punkten nur noch die Tangentengleichung aufstellen. Eine Gerade ist definiert durch . Wir kennen y, Die Steigung k und auch x - somit können wir uns das d berechnen: . In unserem Fall ist und damit haben wir auch schon die Lösung für unsere ersten zwei Tangenten:
Jetzt schauen wir uns das ganze noch für an:
Im Prinzip das selbe Prozedere wie, nach ein bissl umformen kommen wir auf: . Wir setzen das wieder in die Ausgangsfunktion ein:
. Macht man das y explizit (Herausheben, durch 36 dividieren, Wurzel ziehen), kommen wir auf .
Damit haben wir jetzt auch die zwei Punkte der Ellipse, an denen die Steigung -1 beträgt - Nämlich:
Wieder das d berechnen:
Damit haben wir auch die anderen zwei Tangenten gefunden:
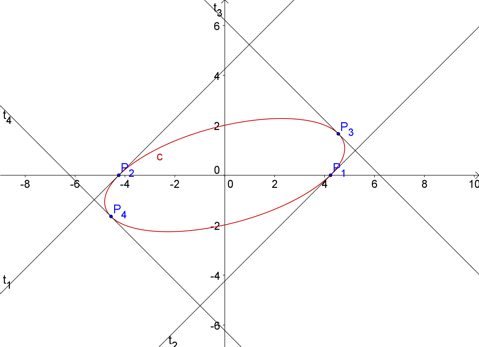
Wir tragen das Ganze nun noch in das Mathe-Programm unserer Wahl ein, um zu sehen, ob das auch hinkommen kann:
Sieht doch gar nicht so schlecht aus, würd ich mal sagen :)
Links[Bearbeiten | Quelltext bearbeiten]
Siehe Diskussion Informatik-Forum WS07 Beispiel 121