TU Wien:Analysis VU (diverse)/Übungen 2024S/Beispiel 348
Gegeben sei die Funktion mit
Zeigen Sie: ist an der Stelle unstetig, aber an dieser Stelle existieren alle Richtungsableitungen und sind identisch 0.
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
Lösungsvorschlag von andrey[Bearbeiten | Quelltext bearbeiten]
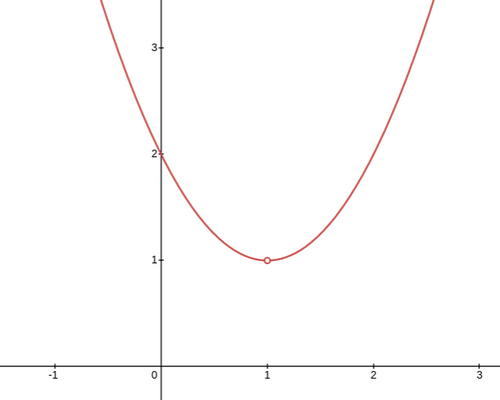
Beginnen wir mit dem, dass wir die Angabe entschlüsseln. Es ist eine Parabel mit Scheitelpunkt im (1, 1) in impliziter Form gegeben. Explizite Gleichung dieser Parabel lautet , auf die wir später noch zu sprechen kommen werden. Die Funktion nimmt also den Wert 1 für alle Punkte auf den Ästen der Parabel an und 0 andernfalls. Die einzige Ausnahme zu dieser Regel ist der Scheitelpunkt selbst, wo die Funktion wegen der verletzten Bedingung ebenfalls den Wert 0 annimmt.
Stetigkeit[Bearbeiten | Quelltext bearbeiten]
Zur Erinnerung: Eine Funktion ist genau dann stetig, wenn für eine beliebige Folge der Grenzwert der Funktionswerte gleich der Funktion der Grenzwerte ist. Um die Stetigkeit zu widerlegen, müssen wir also eine Folge finden, die selbst zu konvergiert, der Grenzwert der Funktionswerte jedoch ungleich ist.
Wir betrachten nun die Folge . Klarerweise liegt jedes der Folgenglieder auf den Ästen der Parabel und die Folge konvergiert zu , wodurch für alle gilt. Die Funktion ist also nicht stetig, weil ist.
Richtungsableitungen[Bearbeiten | Quelltext bearbeiten]
Die Definition der Richtungsableitung an der Stelle lautet , wo für einen beliebigen Einheitsvektor steht. Wenn wir nun für einsetzen und vereinfachen, erhalten wir . Konzeptuell entspricht einer Geraden durch den Punkt mit der Richtung , auf der abhängig von dem Wert ein Punkt herauf und herunter verschoben wird. Da eine Gerade und eine Parabel maximal zwei Schnittpunkte haben können, wird für fast alle genau 0 sein.
Demzufolge existieren alle Richtungsableitungen und sind identisch 0.