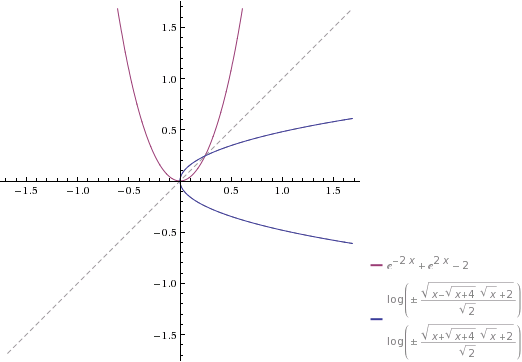TU Wien:Analysis VO (Karigl)/Prüfung 2013-11-29

Aufgabe 1: Funktion, Potenzreihenentwicklung

$f(x)=e^{2x}+e^{-2x}-2$

Graphen zeichnen von $f(x)$ und deren Umkehrfunktion $f(x)^{-1}$ (Wo ist diese überhaupt definiert?). Potenzreihenentwicklung der Funktion angeben (unter Verwendung der Exponentialreihe von $e^{x}$) bei $x_{0}=0$

Lösungsvorschlag

Skizze via WolframAlpha:

Berechnen der Umkehrfunktion scheint hier nicht gefragt zu sein, und da ich das zieml. schwer finde, würde ich in diesem Fall einfach die Spiegelung an der y=x-Achse als Lösungsweg heranziehen.

Definitionsbereich offensichtlich 0 bis $\infty$

Exponentialreihe:

$e^{x}=\sum _{n\geq 0}{\frac {x^{n}}{n!}}$

Daraus folgt:

$e^{2x}+e^{-2x}-2=\sum _{n\geq 0}{\frac {(2x)^{n}}{n!}}+\sum _{n\geq 0}{\frac {(-2x)^{n}}{n!}}-2=$

${\frac {1}{1}}+{\cancel {\frac {2x}{1!}}}+{\frac {4x^{2}}{2!}}+{\cancel {\frac {8x^{3}}{3!}}}+{\frac {16x^{4}}{4!}}+{\cancel {\frac {32x^{5}}{5!}}}+...$

${\frac {1}{1}}-{\cancel {\frac {2x}{1!}}}+{\frac {4x^{2}}{2!}}-{\cancel {\frac {8x^{3}}{3!}}}+{\frac {16x^{4}}{4!}}-{\cancel {\frac {32x^{5}}{5!}}}+...-2=$

$2\sum _{n\geq 0}{\frac {2^{2n}x^{2n}}{(2n)!}}-2=2\sum _{n\geq 0}{\frac {(2x)^{2n}}{(2n)!}}-2$

Edit: Es gilt: $cosh(x)={\frac {1}{2}}*(e^{x}+e^{-x})$
Damit kann man das Gesamtergebnis noch vereinfachen auf $2*cosh(2x)-2$

Aufgabe 2: Funktion

$f(x)={\frac {3}{2e^{2}}}\ -xe^{x}$

Zeigen, dass die Funktion im Intervall $I=[-2,0]$ konkav ist. Außerdem die Fläche unter der Funktion ausrechnen (von -2 bis 0).

Aufgabe 3: Differentialgleichung

Differentialgleichung 1. Ordnung lösen:

$xy'+y=3x^{2}-2$

Wie lautet die partikuläre Lösung mit der Anfangsbedingung $y(1)=4$?

Aufgabe 4: Theorie

Differentialrechnung in mehreren Variablen: Definieren der 3 Begriffe mit je einem Beispiel.

• Partielle Ableitungen
• Richtungsableitung
• Gradient

Aufgabe 5: Theorie

Theoriefragen zum ankreuzen (keine, eine oder mehrere richtige Antworten möglich).

1. Für eine Folge $a_{n}$ gilt:

   • $\forall \varepsilon >0:\forall N(\varepsilon )\in \mathbb {N} :\forall n>N(\varepsilon ):|a_{n}-a|<\varepsilon$
   • $\forall \varepsilon >0:\exists N(\varepsilon )\in \mathbb {N} :\forall n>N(\varepsilon ):|a_{n}-a|<\varepsilon$
   • $\exists \varepsilon >0:\forall N(\varepsilon )\in \mathbb {N} :\forall n>N(\varepsilon ):|a_{n}-a|<\varepsilon$

2. Die Folge $a_{n}=...$ ist... (?? Die Folge fällt mir im Moment nicht ein. Irgendwas mit einem x unter dem Bruch...)

   • monoton
   • beschränkt
   • konvergent

3. Die Folge $a_{n}=(-1)^{n+1}$ ist...

   • monoton
   • beschränkt
   • konvergent

4. Ist die Reihe $\sum a_{n}$ konvergent, dann auch die Folge $a_{n}$

   • Ja
   • Nein

5. ... (Ich glaube eine Frage fehlt noch?!)

Kommentar

Habe ich etwas falsch wiedergegeben, einfach ausbessern. Und wem das fehlende Zeugs noch einfällt, einfach hinschrieben! :-) --Filzstift (Diskussion) 14:44, 30. Nov. 2013 (CET)

Materialien

Neues Material hinzufügen

S

• skizze bsp 1.gif (details)