TU Wien:Dependable Systems VU (Poledna)/Prüfungsordner

Die Zusammenfassung ist in der Datei:TU Wien-Dependable Systems VU (Poledna) - latex fragen.pdf vollständig beinhaltet!

nachdem die Prüfungsfragen mMn quer in den Foren verstreut sind und nicht leicht auffindbar bzw. erweiterbar sind, hab ich mal die Seite angelegt in der Hoffnung, dass sich auch andere finden, die die Fragen ergänzen

Der Grundstock kommt aus dem Informatik- Forum und dieser Ausarbeitung

Alle diese Fragen sind auch unter Datei:TU Wien-Dependable Systems VU (Poledna) - latex fragen.pdf zu finden.

Kapitel 1

Failure vs. Error vs. Fault

Ein Failure ist ein Event, das auftritt, wenn der tatsächliche Service vom korrekten Service abweicht. Ein Failure ist also eine Transition (Übergang) vom korrekten zum fehlerhaften Service. Tritt ein Failure auf, weicht der externe Zustand vom korrekten Zustand ab. Die Abweichung des Zustands nennt man Error. Den festgestellten oder angenommenen Grund für den Error nennt man Fault.

Kapitel 2

Was bedeutet Dependability?

Dependability ist die Vertrauenswürdigkeit eines Computersystems, so dass es vertretbar ist sich auf die zur Verfügung gestellten Services zu verlassen.

Reliance: Man kann sich darauf verlassen, dass

• sich das System gemäß den Spezifikationen verhält
• das System Hazards (=Verhalten, das zu unerwünschten Konsequenzen führen kann) vermeiden kann.

die wichtigsten attribute (reliability, availability, safety, security)?

• Reliability (Funktionsfähigkeit): Verlässlichkeit bezogen auf Kontinuität des Service. R(t) ist die Wahrscheinlichkeit, dass das System über eine Periode t hinweg ununterbrochen zur Verfügung steht
• Availability (Verfügbarkeit): Verlässlichkeit bezogen auf die Verfügbarkeit zu einem bestimmten Zeitpunkt: A oder V ist der Prozentsatz der Zeit, zu dem das System gemäß den Spezifikationen funktioniert.
• Safety (Sicherheit): Verlässlichkeit bezogen auf das Vermeiden katastrophaler Auswirkungen: S(t) ist die Wahrscheinlichkeit, dass ein bestimmtes katastrophales Verhalten innerhalb einer Periode t nicht auftritt.
• Security (Vertraulichkeit): Verlässlichkeit bezogen auf das Verhindern von unerlaubtem Zugriff auf Informationen.
  • Secrecy: wer kann Daten lesen
  • Integrity: wer kann Daten ändern
  • Availability: für wen ist es möglich, die Verfügbarkeit eines Systems zu verringern
• Maintenance (Wartbarkeit): Möglichkeit das System zu warten

reliability vs. safety

Reliability wird durch funktionale Spezifikationen der Korrektheit der Services beschrieben, Safety durch nichtfunktionale Spezifikationen des Vermeidens von Hazards (=Verhalten, das zu unerwünschten Konsequenzen führt).

Die Auswirkungen einer Safety Verletzung sind im Gegensatz zu den Auswirkungen einer Reliability Verletzung katastrophal.

Um Safety bzw. Reliability zu erreichen werden unterschiedliche Methoden des Systemdesigns angewandt. Oft stehen die Ziele in Konflikt miteinander (z.B. Zugsignale: alle Ampeln auf rot ist sicher, aber kein Zug kann fahren, wodurch das Zugsystem nicht funktionsfähig ist).

Wenn es keinen sicheren, nichtfunktionalen Systemzustand gibt (d.h. das System ist fail-operational), sind Safety und Reliability jedoch eng verwandt (z.B. FlybyWire).

reliability vs. availability

Availability ist als Kenngröße nur dann relevant, wenn die Möglichkeit der Wartung existiert.

Beispiel: Bei einem MarsRover muss die Reliability möglichst hoch sein, da das System ab dem ersten Ausfall für immer unbrauchbar wird. Ein System zur MontageAutomation muss jedoch eine gewisse Anzahl an Stücken pro Jahr produzieren, die Availability ist daher der wichtigste Parameter.

Wie hoch ist die Availability in einem System, das nicht gewartet wird

Ist ein System ab dem ersten Ausfall nie wieder einsatzfähig (= Reparatur dauert unendlich lange), beträgt die Availability Null:

$A={\frac {MTTF}{MTTF+MTTR}}={\frac {endlich}{endlich+unendlich}}=0$

• MTTF ... Mean Time to Failure
• MTTR ... Mean Time to Repair

Spezifikation

Alle Attribute der Dependability basieren auf einer Spezifikation. Die Spezifikation und die Analyse des möglichen Verhaltens eines Systems und dessen Auswirkungen sind die schwierigsten Aufgaben beim Design eines dependable Systems.

Eine gute Spezifikation ist:

• exakt
• konsistent
• vollständig
• verbindlich (authoritative)

Oft werden Spezifikationen auf unterschiedlichen Ebenen verwendet, z.B. funktionelle, Reliability, SafetyEbene

Kapitel 3

Assumption Coverage

Jedes Modell/Design basiert auf einer Menge von Annahmen über das Verhalten der Komponenten in der Umgebung. Die Assumption Coverage ist die Wahrscheinlichkeit, dass die Annahmen dem Szenario der realen Welt entsprechen.

Die berechnete Reliability eines Systems muss immer noch mit der Assumption Coverage multipliziert werden. Dadurch kann die Reliability oft empfindlich reduziert werden. Ein System mit perfekter Reliability ist immer nur so gut wie die Assumption Coverage, die der Berechnung der Reliability zugrunde liegt.

Beispiel:

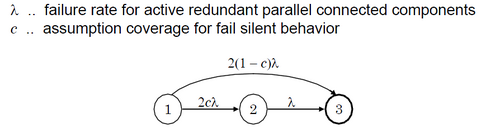
2- Aktive- Redundanz (zwei parallel geschaltete Komponenten) vs. TMR (Triple Modular Redundancy):

Reliability von 2AktiverRedundanz höher, beruht jedoch auf der Annahme, dass sich die Komponenten failsilent verhalten. TMR beruht auf der Annahme, dass sich Komponenten failconsistent verhalten, was einer AssumptionCoverage von annähernd 1 entspricht (byzantinische Fehler sind sehr selten).

Good article on this topic.

Wie sieht die Reliability bei konstanter Fehlerrate aus?

$R(t)=e^{-\lambda t}$

+ Kurve aufzeichnen

Was ist coverage allgemein, und was bedeutet sie beim markov-graphen?

Unter der Abdeckung (Coverage) eines Fehlermodells versteht man die Anzahl von Fehlern, die im Modell beschreibbar sind, zu der Anzahl von tatsächlich auftretenden Fehlern.

• Assumption Coverage: Zu welchem Prozentsatz stimmen die getroffenen Annahmen mit der Realität überein?
• Error Detection Coverage (bei passiver Redundanz): Wie viel Prozent der Fehler einer Komponente werden von einem Switch erkannt, so dass dieser zur funktionierenden Komponente umschalten kann.

Beim Markov- Graph muss die Coverage entsprechend berücksichtigt werden. D.h. die Wahrscheinlichkeit, dass der Fehler innerhalb der failure- semantic liegt, muss bei den "normalen" Übergängen berücksichtigt werden. Mit der Gegenwahrscheinlichkeit führt dann zusätzlich noch eine Kante direkt zum Fehlzustand.

markov property?

Das Verhalten des Systems ist zu jedem Zeitpunkt unabhängig von der Vorgeschichte, abgesehen vom letzten Zustand.

Reliability Growth Model?

Probabilistic Structural Modeling ist für Software nicht gut geeignet, da es bei Software keine ausreichend definierten individuellen Komponenten gibt, die Komplexität sehr hoch ist, keine Unabhängigkeit der Fehler angenommen werden kann (da nur eine CPU und ein Speicherbereich für verschiedene Prozesse existiert), Aspekte der Echtzeitverarbeitung nicht modelliert werden können und Parallelität und Synchronisierung nicht beachtet werden (außer bei GSPNs)

Reliability Growth Models basieren auf der Idee einer Iterativen Verbesserung nach dem Schema testing → correction → retesting

Dabei werden keine Annahmen über die SystemStruktur (insbesondere über die Aufteilung in Komponenten) getroffen.
Z.B. Software reliability growth: SoftwareTest → Aufzeichnen der Zeitperioden zwischen aufeinander folgenden Fehlern → ausbessern der Fehler
Ausgehend von den gemessenen Zeiträumen (Perioden) kann auf die zukünftigen Perioden zwischen zwei Fehlern geschlossen werden (und z.B. als MTTF angegeben werden)

Ziele:

• Disziplinierte und Kontrollierte Verbesserung der Reliability
• Extrapolieren von Zukünftiger Reliability auf Basis der Aktuellen Reliability
• Abschätzen des Aufwands für Test, Verbesserung und ReTest

Vorteile:

• Erlaubt Modellierung von alterungsbedingten Fehlern und DesignFehlern
• Kann für Hardware und für Software eingesetzt werden

Nachteile:

• Die Zuverlässigkeit dieses Modells variiert stark

Warum werden beim Modellieren von zuverlässigen Systemen gerne konstante Fehlerraten angenommen?

Part 3 auf Folie 7. Weitere Erklärungen finden sich in Part 5 auf Seite 12ff.

Kapitel 4

probability/severity?

Das primäre Ziel von Safety ist eine umgekehrt proportionale Beziehung zwischen Wahrscheinlichkeit und Schwere eines Fehlers herzustellen: Wahrscheinliche Fehler sollen keine schwerwiegenden Konsequenzen haben, während Fehler mit katastrophalen Auswirkungen sehr unwahrscheinlich gemacht werden sollen.

Klassen der Severity:

• No Safety Effect
• Minor
• Major
• Hazardous (starke Reduktion der Sicherheit, zu Schaden kommen einer relativ kleinen Gruppe von Personen)
• Catastrophic (Absturz des Flugzeugs)

Klassen der Probability:

• Probable: ein oder mehrere Vorkommen im Leben eines Flugzeugs, p > 10⁻⁵ pro Flugstunde
• Improbable: Fehler tritt wahrscheinlich nicht im Leben eines Flugzeugs auf, könnte aber bei einigen wenigen Flugzeugen eines Typs auftreten, 10⁻⁹ < p < 10⁻⁵
• Extremely Improbable: Fehler tritt wahrscheinlich kein einziges mal in irgendeinem Flugzeug des selben Typs auf, p < 10⁻⁹

Kapitel 5

Failure Modes?

Fehler sind definiert nach dem Verhalten, das an der Systemschnittstelle beobachtet werden kann.

Hierarchische Klassifikation:

• Byzantinische, Arbitrary (beliebige) Failures: keine Einschränkung des Verhaltens, z.B. kann das Fehlverhalten von zwei unterschiedlichen (korrekt arbeitenden) Komponenten unterschiedlich wahrgenommen werden.
• Authentification detectable byzantine Failures: wie Byzantinisch, jedoch können Nachrichten von anderen Systemen nicht gefälscht werden (nur sinnvoll bei verteilten Systemen)
• Performance Failures:Resultate sind korrekt bezogen auf den Wert, jedoch treffen sie zu früh oder zu spät ein (early oder late failures)
• Omission Failures: Resultate kommen entweder rechtzeitig oder nie an (Spezialfall von PerformanceFailures)
• Crash Failures: Bei Auftreten eines Fehlers sendet die Komponente in der Folge keine Resultate mehr. (Spezialfall von OmissionFailures)
• FailStop Failures: Spezialfall von CrashFailures, der von anderen Systemen erkannt werden kann. Außerdem kann der letzte gültige Zustand von einem stabilen Datenspeicher gelesen werden.

Klassifikation nach Auftreten

• Value Failures (byzantinisch, a.d. byzantinisch)
• Timing Failures (performance, omission, crash, failstop)

Klassifikation nach Wahrnehmung des Users

• Consistent Failures: von allen Usern gleich wahrgenommen (performance, omission, crash, failstop)
• Inconsistent Failures: von unterschiedlichen Usern unterschiedlich wahrgenommen (byzantinisch, a.d. byzantinisch)

Klassifikation nach Auswirkungen auf die Umgebung

• Benign Failures: Höhe des Schadens im Fehlerfall ungefähr gleich des Nutzens des funktionsfähigen Systems
• Catastrophic failures: Schaden im Fehlerfall wesentlich Höher als Nutzen des funktionsfähigen Systems, insbesondere Schaden für menschliche Gesundheit/ menschliches Leben.

Arrhenius Equation?

Gibt den Zusammenhang zwischen Aktivierungsrate von Fehlern und Temperatur von Halbleiterbauteilen an:

$R=R_{0}\cdot e^{-{\frac {E_{A}}{k\cdot T}}}$

$R_{0}$... Konstante
$E_{A}$... Aktivierungsenergie [eV]
T... Absute Temperatur [K]
k... Boltzmannkonstante $8.6\cdot 10^{-5}{\frac {eV}{K}}$

Für Software nicht anwendbar, da nicht bekannt ist, wie man „Stress“ für Software charakterisieren und simulieren kann.

Accelerated Stress Testing?

Wird verwendet um die InfantMortalityFailures schon vor der Auslieferung zu erkennen, und um die zu erwartende Fehlerrate mit relativ kurzen Testperioden abschätzen zu können.

Möglichkeiten des künstlichen Beschleunigens von FehlerauftrittsIntervallen:

• Erhöhung der Temperatur
• Verringerung der Temperatur
• schnelles Abwechseln von hohen und niedrigen Temperaturen
• Erhöhung der Spannung
• Erhöhung der Temperatur und der Spannung
• Erhöhung der Temperatur, Spannung und Feuchtigkeit
• Beschießen mit AlphaPartikeln

Für Software nicht anwendbar, da nicht bekannt ist, wie man „Stress“ für Software charakterisieren und simulieren kann.

Safety Analysis (auch die einzelnen Methoden, also PHA HAZOP usw. was bedeuten Abkürzungen, kurz wies funktioniert und Vor- und Nachteile)?

Die Safety- Analyse beschäftigt sich mit dem gesamten Lebenszyklus eines Projekts, von der Spezifikation bis zur Modifikation. Wichtig sind Definitionen von Zuständigkeiten, Kommunikation mit anderen Gruppen, vollständige Dokumentation, Analyse komplexer Prozesse und ManagementProzeduren (Meetings, TimeScheduling, etc.).

Hauptfragen der Safety- Analysis sind:

• welche Hazards sind möglich (Hazard Analysis)
• wie kann es zu diesen Hazards kommen (Accident Sequencing)
• wie wahrscheinlich kommt es zu Hazards (Quantitative Analyse)

Preliminary Hazard Analysis (PHA)

Stellt die erste Phase in jeder SafetyAnalyse dar. System Hazards, kritische Zustände und Failure- Modes werden definiert, kritische Elemente identifiziert und Konsequenzen und Wahrscheinlichkeiten der hazardous Events bestimmt und festgelegt. Die gewonnenen Erkenntnisse sind Thema genauerer Analyse in darauf folgenden Phasen.

Hazards and Operability Study (HAZOP)

Systematisches Suchen nach Abweichungen, die zu Hazards führen könnten. Dazu wird für jeden Teil des Systems eine Spezifikation der „Intention“ erstellt, danach kann das System nach Abweichungen durchsucht werden. Es werden Guide Words anhand einer CheckListe abgearbeitet, um verschiedene Typen von Abweichungen zu spezifizieren: NO, NOT, MORE, LESS, AS WELL AS, PART OF, REVERSE, OTHER THAN

Die Analyse wird von einem Team bestehend aus unterschiedlichen Spezialisten durchgeführt.

Diese Methode ist gut um die Kommunikation zwischen beteiligten Personen zu erhöhen und um Ausgangspunkte für detaillierte Studien zu schaffen, jedoch ist sie nicht gut Standardisiert.

Action Error Analysis (AEA)

Beschäftigt sich mit den potentiellen Fehlern, die Menschen bei der Verwendung, Wartung, Kontrolle und Überwachung machen können.

• Die einzelnen Schritte in Bedienungsabläufen werden aufgelistet,
• für jeden Schritt eine Liste möglicher Fehler erstellt,
• die Konsequenzen der Fehler beurteilt
• sowie deren Ursache (gewisse Aktionen nicht durchgeführt, in Falscher Reihenfolge durchgeführt, etc..) bestimmt.

Darauf aufbauend kann analysiert werden, wie man Kontrolle über diese Ursachen bekommen kann.

AEA beschäftigt sich nicht mit den Gründen für Bedienungsfehler.

AEA ist besonders für Software im Bereich des User Interface Design wichtig.

Fault Tree Analysis (FTA)

Graphische Repräsentation von Kombinationen, die zu Hazards führen können. Dabei wird vom Hazard als Wurzel des Baums ausgegangen, die Verzweigungen finden an ODER- oder UND- Symbolen statt. Die einzelnen Knoten sind Events.

Kann als quantitative Methode verwendet werden.

Einschränkungen:

• Es wird angenommen, dass Fehler binär sind, also eine Komponente entweder komplett oder garnicht ausfällt.
• Bäume werden schnell sehr groß und unverständlich,
• sind nicht mathematisch eindeutig.

Event Tree Analysis (ETA)

Etwaige Konsequenzen von Fehlerursachen und Faults werden als Events modelliert. Ausgehend von grundlegenden Events werden die möglichen Konsequenzen des Events bis hin zu möglichen Fehlern abgeleitet. Umgekehrte Vorgehensweise wie bei FTA: es wird mit den Events begonnen. Kann als quantitative Methode verwendet werden.

Einschränkungen: Detaillierte Analysen können wegen des Großen Umfangs nicht erstellt werden, parallele Sequenzen, unvollständige, zu frühe oder zu späte Aktionen werden als Fehlerursache nicht in Betracht gezogen.

Failure Modes and Effect Analysis (FMEA)

Der Designer muss systematisch die Fragen „Wie kann eine Komponente ausfallen?“ und „Was passiert in diesem Fall?“ beantworten. Dazu wird das System in Komponenten zerlegt (→ Block Diagram), für die die FailureModes, die Ursache und die Bedeutung von Fehlern identifiziert werden. Es wird ermittelt, wie Failures erkannt werden können und wenn notwendig Empfehlungen zu geeigneten Kontrollmaßnahmen gegeben.

Die Analyse wird durch standardisierte Tabellen unterstützt.

Einschränkungen: Kombinationen von technischen und menschlichen Fehlern werden oft nicht bedacht und es ist schwierig gleichzeitige Fehler zu Analysieren.

Failure Modes, Effect and Criticality Analysis (FMECA)

Wie FMEA, jedoch wird besonderes Augenmerk auf CriticalityAspekte gelegt.

(Criticality: Wie viel Spielraum besteht zwischen korrektem Verhalten laut Spezifikation und Hazards)

CauseConsequence Analysis

Kombination aus FTA und ETA: Startpunkte der Analyse sind kritische Events, ETA wird Verwendet um die Konsequenzen, FTA um die Ursachen zu ermitteln. Diese Methode ist sehr flexibel und gut dokumentiert, hat jedoch viele Nachteile der FTA (Baum wird schnell zu groß und unübersichtlich, bestimmte Kombinationen werden nicht bedacht, etc.)

Kapitel 6

maintenance (warum besser als fault-tolerance)?

Maintenance macht ein System zwar komplexer, aber in wesentlich geringerem Ausmaß als FaultTolerance. Dadurch sinkt auch die Wahrscheinlichkeit von DesignFaults. ErrorDetection wird benötigt, jedoch kein FaultTreatment auf Systemebene

Allerdings ist Maintenance als Mittel zu Dependability nur möglich, falls SystemDownTimes erlaubt sind (d.h. es handelt sich um ein FailStop- oder FailSafe- System wie z.B. Zugsignale, nicht jedoch um ein FailOperational- System wie z.B. Flugzeug).

Außerdem kann nur begrenzte Reliability erzielt werden. Preventive Maintenance ist nur dann sinnvoll möglich, wenn die auswechselbaren Komponenten konstante oder steigende FailureRates haben und die InfantMortality gut kontrolliert werden kann.

Replika Determinismus?

Definition:

Korrekte Replikate erzeugen korrespondierende ServiceOutputs und/oder ServiceStates unter der Annahme, dass alle Server der Gruppe im gleichen Zustand starten und korrespondierende Service- Requests innerhalb eines gegebenen Zeitintervalls ausführen. Diese Art von Replika- Determinismus wird Replica Control genannt.

Es ist notwendig, dass replizierte Komponenten eines systematisch Faulttoleranten Systems (Fault Tolerance wird unabhängig von Applikationspezifischem Wissen implementiert, also durch Replikation) im fehlerfreien Fall korrespondierende Werte zu korrespondierenden Zeitpunkten liefern, das Verhalten der Komponenten also konsistent ist. Dies ist notwendig, um zwischen fehlerhaftem und korrektem Verhalten unterscheiden zu können.

Mögliche Ursachen für Replika- Nichtdeterminismus:

• unterschiedliches Runden analoger Eingangsgrößen
• unterschiedliche Wahrnehmung der Reihenfolge von Ereignissen durch nicht perfekt synchronisierte lokale Uhren
• unterschiedliche Wahrnehmung der Reihenfolge von Ereignissen durch unterschiedliche Message Transmission Delays
• Inkonsistente Information über die Gruppenmitgliedschaft von Replikationen
• nichtdeterministische Programmkonstrukte (Zufallsgenerator, Konstrukte zur Kommunikation, Synchronisation, etc.)
• Entscheidungen, die auf lokalen Informationen beruhen (z.B. CPULoad, lokale Zeit)
• Unterschiedliche TimeoutEntscheidungen durch ClockDrifts
• Dynamische Scheduling- Entscheidungen
• Unterschiedliche Rundung von Real- Zahlen auf unterschiedlichen Implementierungen

Kann Replika- Nichtdeterminismus nicht verhindert werden, müssen Agreement Protokolle verwendet werden. (Auch diese können das Problem jedoch nicht vollständig lösen)

Was ist Konsistenz?

Konsistenz im Allgemeinen bezeichnet die Abwesenheit von Widersprüchen. Ein Zustand in einem verteilten System wird Konsistent genannt, wenn er während der Ausführung des Systems existieren könnte. (Part 6, Seite 74)

Was ist Konsistenz bei Replica?

Konsistenz ist der Zustand, in dem sich alle korrekten Prozessoren einer Gruppe auf einen Wert geeinigt haben und alle Entscheidungen endgültig sind. (Vorlesungsfolien, part6)

Ein Zustand in einem verteilten System ist konsistent, wenn er ohne das Auftreten von Fehlern existieren könnte.

recovery lines?

Eine Menge von RecoveryPoints bildet eine Recovery Line (= ein konsistenter Zustand), wenn er folgende Bedingungen erfüllt:

• Die Menge enthält genau einen RecoveryPoint für jeden Prozess.
• Keine Nachricht wird von Prozess P vor dessen RecoveryPoint empfangen, wenn sie nicht auch vor dessen RecoveryPoint gesendet wurde. (No Orphan Message)
• Keine Nachricht wird von Prozess P vor dessen RecoveryPoint gesendet, wenn sie nicht auch vor dessen RecoveryPoint empfangen wurde. (No lost Message)

consensus protocols?

Wird bei Strictly Distributed Replica Control (alle Replikate sind Gleichwertig) benötigt, um Konsistenz unter den Replikaten zu erzeugen.

Ein Konsens- Protokoll muss folgende Eigenschaften aufweisen:

• Konsistenz: Jeder Knoten muss zur gleichen Entscheidung kommen
• Nicht- Trivialität: Der Wert, auf den sich die Knoten einigen, muss der Eingabewert eines Knoten der Gruppe oder eine Funktion der einzelnen EingabeWerte sein
• Terminierung: Jeder Knoten trifft seine Entscheidung in endlicher Zeit.

reliable broadcast?

Wird bei Central Replica Control (eines der Replikate hat eine Führungsposition) benötigt, um Konsistenz unter den Replikaten zu erzeugen. Ein Reliable Broadcast muss folgende Eigenschaften aufweisen:

• Konsistenz: Alle Knoten müssen den selben Wert erhalten, dieser Wert ist endgültig
• Nicht- Trivialität: Wenn der Transmitter nicht fehlerhaft ist, erhalten alle Knoten den Eingangswert des Transmitters
• Terminierung: Jeder Knoten trifft seine Entscheidung in endlicher Zeit.

Common Mode Failure? Diagnose

Common Mode Failures treten dann auf, wenn die Ursachen für einen Failure von unterschiedlichen Komponenten nicht statistisch unabhängig sind.

Beispiel: Mehrere Knoten an einem Bus, ein Knoten der ausfällt verhält sich nicht failsilent („Babbling Idiot“) Die Kommunikation aller Knoten wird gestört und alle → Resultate werden unbrauchbar.

Mit der Common Mode Analysis versucht man zu beweisen, dass als unabhängig angenommene Failures wirklich statistisch unabhängig sind. Dabei werden auch die Auswirkungen von Design, Fertigung und Wartung analysiert.

wieviele nodes braucht man um byzantinische fehler zu erkennen?

man braucht

• 3k+1 Komponenten, um k byzantinische Fehler zu tolerieren
• 2k+1 Komponenten, um k Performance- Fehler zu tolerieren
• k+1 Komponenten, um k Crash- oder Omission- Fehler zu tolerieren

Für Performance- und byzantinische Fehler werden k+1 identische Resultate benötigt

+ erklärung! (zb. warum 3k+1 f. byzantinische fehler, muss bei crash failures auf alle entscheidungen gewartet werden oder kann die erste gleich verwendet werden)

Consistency algorithm?

sind geeignet, um für Konsistenz unter den funktionsfähigen Knoten zu sorgen, selbst wenn sich k Knoten byzantinisch verhalten (bei einer Anzahl von n>=3k+1 Knoten insgesamt).

Beispiel 1:

Annahmen über das Kommunikationssystem:

• Alle Nachrichten werden korrekt übertragen
• Der Empfänger weiß, wer der Absender einer Nachricht ist
• Die Abwesenheit einer Nachricht kann erkannt werden

Der Transmitter sendet seinen Wert an alle Empfänger. Diese senden den empfangenen Wert, bzw. den Default- Wert (falls sie keinen Wert vom Transmitter erhalten haben) an alle anderen Knoten. Jeder Knoten entscheidet nach der Mehrheit der empfangenen Werte.

Beispiel 2:

Es werden signed Messages verwendet, um byzantinisches Verhalten zu erkennen

Lässt sich in jedem System Consensus herstellen?

Asynchrone Systeme könnnen keinen Konsens mit einem deterministischen Algorithmus herstellen, weil es unmöglich ist zwischen einer späten Rückmeldung oder einem Prozessor- Crash zu unterscheiden.

Es gibt aber probabilitische Protokolle mit denen ein Konsens in einer (zu erwartenden) konstanten Number von Durchgängen hergestellt werden kann. (coin- flipping)

In synchronen Systemen geht das schon, sofern die Kriterien für die fault- tolerance erfüllt sind.

Eigenschaften eines synchronen Systems

Ein System wird synchron genannt, wenn alle Prozessoren synchron sind und die Kommunikations- Verzögerung beschränkt ist.

Ein Prozessor ist synchron, wenn er zumindest einen Schritt in einem Realtime- Schritt durchführt.

Ein Kommunikation- Verzögerung ist beschränkt, wenn eine Nachricht spätestens nach einer bestimmten Zeit eintreffen muss.

(sihe auch Seite 29 in den Folien)

Unterschied zwischen Systematischer und Anwendungsspezifischer Fehlertoleranz (+ Vor- und Nachteile)

(Seite 10ff)

Im Gegensatz zur systematischen Fehlertoleranz, welch versucht durch die Replikation gleichartiger Komponenten Fehler zu erkennen und zu tolerieren, baut die anwendungsspezifische Fehlertoleranz auf ein Modell der Wirklichkeit auf. Anhand dieses Modells werden bei der anwendungsspezifischen Fehlertoleranz Plausibilitätsprüfungen abgeleitet, welche Fehler erkennen sollen. Des weiteren kann auf Basis des Modells eine Schätzung des Zustands und dadurch ein (eingeschränkter) Betrieb erfolgen.

Anwendungsspezifische Fehlertoleranz: Der physikalische Prozess, mit dem das Computersystem interagiert unterliegt gewissen physikalischen Gesetzen und dadurch Beschränkungen. Diese Beschränkungen können im Computersystem implementiert werden um Fehler zu identifizieren. Die Plausibilitätsprüfungen sind dabei anwendungsspezifisch und ermöglichen ein "fail-stop" Verhalten des Systems. Um ein fail-operational Verhalten des Systems zu implementieren kann zusätzlich eine Abschätzung des Betriebszustandes (state-estimation) erfolgen.

Vorteile:

• forward- und backward-recovery möglich
• Keine zusätzlichen Kosten für replizierte Komponenten
• Kein Zuwachs an Komplexität auf Systemebene

Nachteile:

• Die Fehlererkennung ist durch eine Grauzone eingeschränkt
• Für manche Anwendungsgebiete existieren keine brauchbaren Plausibilitätsprüfungen
• Die Qualität des bereitgestellten Dienstes ist im Fehlerfall geringer als im Normalbetrieb
• Die korrekte Funktion des Systems hängt von der Schwere des Fehlers ab
• Zuwachs an anwendungsspezifischer Komplexität
• Anwendung und Fehlertoleranz sind stark verflochten

Systematische Fehlertoleranz: Bei der systematischen Fehlertoleranz werden keine Annahmen über den zugrundeliegenden physikalischen Prozess getroffen sondern eine etwaige Abweichung replizierter Komponenten zur Fehlererkennung eingesetzt. Replika müssen daher im Normalfall korrespondierende Ergebnisse liefern um Abweichungen im Fehlerfall erkennen zu können (replica-determinism). Diese Eigenschaft muss durch ein agreement protocol sichergestellt werden.

Bei der systematischen Fehlertoleranz wird davon ausgegangen, dass manche, aber nicht alle Komponenten fehlerhaft sind. (n-resiliency) Ein fail-stop Verhalten kann hier durch die Divergenz von Ergebnissen erreicht werden, ein fail-operational Verhalten durch mehrfach redundante Auslegung von Subsystemen.

Vorteile:

• Kein Anwendungswissen erforderlich
• Keine state-estimation erforderlich
• Unabhängige Bereiche der Applikation
• Qualität des bereitgestellten Dienstes ist unabhängig von Fehlern
• Keine Steigerung der anwendungsspezifischen Komplexität
• Fehlertoleranz kann transparent erfolgen

Nachteile:

• Benötigt Replica-Determinismus
• Die korrekte Funktion des Systems hängt von der Anzahl der eingesetzten Komponenten ab
• Nur backward-recovery
• Zusätzliche Kosten für replizierte Komponenten
• Steigerung der Komplexität auf der Systemebene

(noch) nicht zugeordnet

fail silent/fail consistent?

(Übernommen und Überarbeitet von: Echzeitsysteme )

Die Anzahl an benoetigten redudanten Komponenten welche bei Ausfall einer Komponente das fortlaufen des Systems sichern, ist abhaengig von der Art des auftretenden Fehlers. Man unterscheidet hier zwischen consisten failure und inconsistent failure.

Bei consisten failure ist der aufgetretende Fehler fuer alle Beobachter ident.
Bei den consistent failures kann man weiter fail silent failure und crash failure unterscheiden. Ein fail silent failure bedeutet das die fehlerhafte Komponente nicht mehr ansprechbar ist bzw. auch keine weiteren noch funktionierenden Systme negativ beeinflusst, also silent. Bei crash failure wuerde der Ausfall einer Komponenten den Absturz des gesammten Systems bedeuten.

Bei inconsitent failurs kann dieser fuer die Beobachter verschieden sein.
Inconsistent Failure sind die "teuersten" Fehler, da hier am meissten redudante Komponenten benoetigt werden. Incosistent Failure werden auch two-faced failurs, malicious failures, oder Byzantine failures genannt.

Bei k auftetenden fehlerhaften Kompoenten, benötigt man N redudante idente? Komponenten:

• fail-silent: k+1
• fail-consistent: 2k+1
• fail-malicious/byzantine: 3k+1

fault-tolerance by self-stabilization

Ein verteiltes System S ist self-stabililizing unter Berücksichtigung eines globalen Prädikats P, wenn es folgende beiden Kriterien erfüllt:

• Closure: P ist geschlossen unter der Ausführung von S, so dass wenn P in S eingeführt wird es nicht mehr verfälscht werden kann.
• Convergence: Ausgehend von einem beliebgen globalen Zustand muss gewährleistet werden, dass S in endlichen Zustandsübergängen einen globalen Zustand erreicht wo P is satisfied.