TU Wien:Diskrete Mathematik für Informatik UE (Gittenberger)/Übungen WS13/Beispiel 21

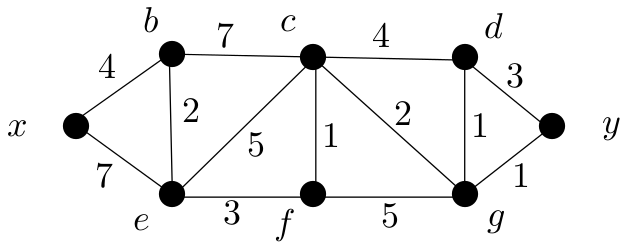
Use Dijkstra’s algorithm to determine d(x, y) in the following graph.

Solution[Bearbeiten | Quelltext bearbeiten]

x	b	c	d	e	f	g	y	Node	Predecessor
0	∞	∞	∞	∞	∞	∞	∞	x	-
	4	∞	∞	7	∞	∞	∞	b	x
		11	∞	6	∞	∞	∞	e	b
		11	∞		9	∞	∞	f	e
		10	∞			14	∞	c	f
			14			12	15	g	c
			13				13	d	g
							13	y	g

The shortest path from x to y is x-b-e-f-c-g-y with length 13.

x	b	c	d	e	f	g	y	Node	Predecessor
0	∞	∞	∞	∞	∞	∞	∞	x	-
	4	∞	∞	7	∞	∞	∞	b	x
		11	∞	6	∞	∞	∞	e	b
		11	∞		9	∞	∞	f	e
		10	∞			14	∞	c	f
			14			12	15	g	c
			13				13	d	g
							13	y	g

x	b	c	d	e	f	g	y	Node	Predecessor
0	∞	∞	∞	∞	∞	∞	∞	x	-
	4	∞	∞	7	∞	∞	∞	b	x
		11	∞	6	∞	∞	∞	e	b
		11	∞		9	∞	∞	f	e
		10	∞			14	∞	c	f
			14			12	15	g	c
			13				13	d	g
							13	y	g

x	b	c	d	e	f	g	y	Node	Predecessor
0	∞	∞	∞	∞	∞	∞	∞	x	-
	4	∞	∞	7	∞	∞	∞	b	x
		11	∞	6	∞	∞	∞	e	b
		11	∞		9	∞	∞	f	e
		10	∞			14	∞	c	f
			14			12	15	g	c
			13				13	d	g
							13	y	g