TU Wien:Diskrete Mathematik für Informatik UE (Gittenberger)/Übungen WS13/Beispiel 31

Let $G$ be an Eulerian graph and $H$ be a subdivision of $G$. Is $H$ Eulerian? Suppose that $G$ is Hamiltonian. Does this imply that $H$ is Hamiltonian as well?

Solution

We get a subdivision of a graph if we split edges in two parts by adding a node between these parts. The degree of the nodes which were already in the graph stays the same. Since each node we add goes between two edges, the degree of each new node is two and therefore even. This means that if all node degrees of a graph were even (Eulerian graph), then all nodes of a subdivisions this graph also have even degree. Therefore for each Eulerian graph $G$ a subdivision $H$ is also Eulerian.

Lets assume we have an Hamiltonian graph $G$. This means that there has to exist a cycle which visits every node exactly once. Now we have two possibilities:

• We subdivide edges, which are not part of the Hamiltonian cycle: Then it is possible that $H$ is not Hamiltonian:

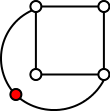
• We subdivide on the Hamiltonian cycle: Then we can construct a new Hamiltonian cycle. Lets say $H_{1}$ is the first step in the process of adding additional nodes on edges of the Hamiltonian cycle in $G$ to get to $H$. We assume the edge we slitted into two parts was $(u,w)$ and we used the node $v$ to split the edge into the new edges $(u,v)$ and $(u,w)$. We can then construct a Hamiltonian path for $H_{1}$ by modifying the Hamiltonian path for $G$. Instead of the edge $(u,w)$ we add the two edges $(u,v)$ and $(v,w)$. By iterating this process for $H_{2},H_{3},\dots$ we are able to construct the Hamiltonian path for the subdivision $H$.

---

I think the solution above is correct for Eulerian graphs, but wrong for Hamiltonian graphs. First of all, the definition of a Hamiltonian graph is "$G$ is Hamiltonian, iff it contains a Hamiltonian cycle" (not a path). Second, note, that there is no need for all edges to be involved into a Hamiltonian cycle. Suppose there is a graph containing only one Hamiltonian cycle, but a few more edges, and one of these edges is subdivided, this will create a graph, that is not Hamiltonian any more.

---

The solution is correct but only valid for graphs where you subdivide along the hamlitonian cycle. If you don't do that, it's easy to find counter evidence:

---

Thanks a lot! I tried to fix the solution above.

Materialien

Neues Material hinzufügen

D

• DiMa w13 31 counter evidence.png (details)