TU Wien:Diskrete Mathematik für Informatik UE (Gittenberger)/Übungen WS13/Beispiel 33

Use a suitable graph model to reformulate the exercise as graph theoretical problem:

Given a subset $A\subseteq R^{2}$ which has area $a$ and two decomposition of $A$ into subsets $A_{1},A_{2}\dots ,A_{m}$ and $B_{1},B_{2},\dots ,B_{m}$ such that all the $A_{i}$ ’s and all the $B_{i}$ ’s have the same area $a/m$. Prove that there exists a permutation $\pi$ of ${1,2,\dots ,m}$ such that for all $i=1,\dots ,m$ we have $A_{i}\cap B_{\pi }(i)\neq \varnothing$.

Solution

For every area $A_{1},A_{2},\dots ,A_{m}$ and $B_{1},B_{2},\dots ,B_{m}$ we draw a node. For every set $A_{i}$ and $B_{j}$ which share a common area ($A_{i}\cap B_{j}\neq \emptyset$) we draw an undirected edge between their nodes. From this construction we get a bipartite graph. To show that there exists a permutation $\pi$ we need to find an edge matching where every node occurs exactly once (perfect matching). The Figure below shows an example for two compositions and a possible permutation $\pi$.

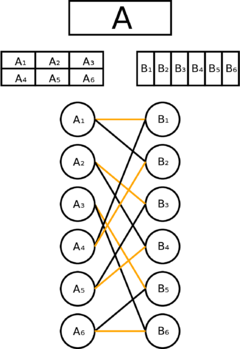
According to König's theorem the number of edges in a perfect matching equals the number of nodes in a minimum vertex cover. Since we need either all nodes $A_{i}$ or $B_{i}$ to get a minimum vertex cover (Why?? Example from Wikipedia: http://upload.wikimedia.org/wikipedia/commons/2/2e/Koenigs-theorem-graph.svg - not every vertex from A or B is used. The only thing I can come up with is, that every vertex is connected to at least one distinct vertex in B (when A = B, so all Ai = Bi) or have additional edges (when moving the areas a little bit, they will still overlap there Bi, but also other areas. But this would already be a proof for the whole thing. Any other ideas? — no nodes of either group are directly connected to each other — we need $m$ nodes to construct a minimal vertex cover. This means a perfect matching with $m$ edges exist. This matching gives us a correct permutation $\pi$ since each node in this edge matching must occur exactly once.

Scheint nicht ganz zu stimmen, siehe: https://math.stackexchange.com/questions/1511777/reformulating-a-problem-as-graph-theoretic

Alternative Solution (suggestion)

Using the graph model from above, let $L=A_{1}\cup \ldots \cup A_{m}$ and $R=B_{1}\cup \ldots \cup B_{m}$. Until now we have a model, and we know that for the permutation to exist, there must be a complete (i.e. perfect) matching in our graph. So we need to show that such a matching exists for all m. Now observe some properties of the graph:

• $|L|=|R|$, since both L and R are decompositions into m parts.
• Every $A_{i}$ is connected to at least one $B_{j}$ - Since both decompositions cover the whole area of A, the area covered by any one element of one decomposition must also be covered in the other decomposition.
• Because every element in L is connected to at least one element in R, we can state that $\forall LP\subseteq L:|\Gamma (LP)|\geq |LP|$, i.e. the neighborhood of every set of elements on the left has at least as many elements as the set itself.

These are exactly the conditions under which a complete matching exists according to Hall's Marriage Theorem - which is known to be true ;) - so we're done here.

Materialien

Neues Material hinzufügen

E

• Exercise 33.png (details)