TU Wien:Diskrete Mathematik für Informatik UE (Gittenberger)/Übungen WS13/Beispiel 34

Reformulate the exercise as graph theoretical problem:

Given a set $A$ with $n$ elements and $B=\{A_{1},A_{2},...,A_{n}\}\subseteq 2^{A}$. Prove that there exists an injective mapping $f:B\rightarrow A$ such that $f(A_{i})\in A_{i}$ for all $i\in \{1,2,...,n\}$ if and only if for all $I\subseteq \{1,2,...,n\}$ the cardinality of $\bigcup _{i\in I}A_{i}$ is at least equal to the cardinality of $I$.

Solution

We construct a bipartite graph by placing a node for every set $A_{i}$ on the left side. Then we place a node for every element of $A$ on the right side. We connect a node for a certain set $A_{i}$ with every node which contains an element of $A_{i}$ with an undirected edge. To get an injective mapping we need to select a complete matching. This is the same task as in the marriage theorem. The elements of the set $A$ represent the men, while $A_{i}$ represents the set that woman $i$ is willing to marry. So to get to a complete matching all unions of the form $\bigcup _{i\in I}A_{i}$ must be greater or equal to the number of sets in the union $I$.

Comment: This has to be proven here, doesn't it? Selfanswering (for other people): No, it hasn't. The iff-part in the description of this exercise refers exactly to the marriage theorem, so this is correct.

To make things clearer we give a small example where we can construct an injective mapping:

$A=\{1,2,3\}$

$B=\{A_{1},A_{2},A_{3}\}\subseteq 2^{A}\quad {\text{e.g. }}B=\{\{1\},\{1,2\},\{2,3\},\}$

$f(A_{1})\in A_{1}\quad f(A_{2})\in A_{2}\quad f(A_{3})\in A_{3}$

The Figure below shows the injective mapping for this example.

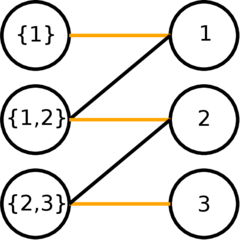
Siehe: https://math.stackexchange.com/questions/1506816/reformulating-a-problem-as-graph-theoretic-problem

Materialien

Neues Material hinzufügen

E

• Exercise 34.png (details)