TU Wien:Diskrete Mathematik für Informatik VO (Drmota)/Prüfung 2015-11-27
1 Generating functions[Bearbeiten | Quelltext bearbeiten]
a) A(z) is the OGF of . Compute the OGF of und
Solution: Either by building difference of b_n and b_n+1, or applying convolution formula
Solution: Differentiate formula for (a_n) = 1, multiply z
b) D(z)
and
for
Solution: Compute difference of d_(n+1) and d_(n), simplify, build the difference again, plug in OGF formula
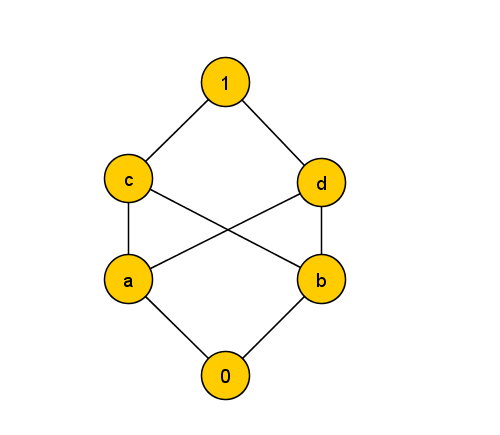
2 Möbius function[Bearbeiten | Quelltext bearbeiten]
a) Calculate Möbiusfunction
Solution: -1 IIRC
b) Relations (c,b) and (d,a) removed, what is the new
Solution: 1 IIRC
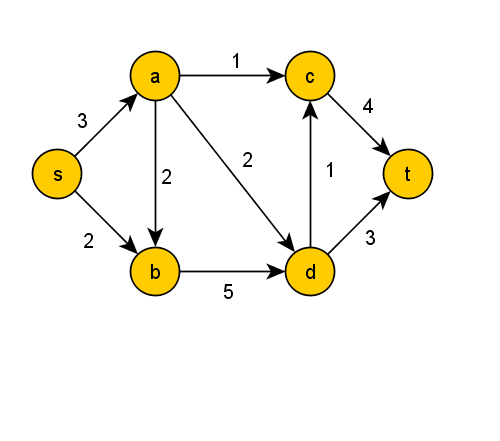
3 Maximal Flow[Bearbeiten | Quelltext bearbeiten]
a) Compute the maximal flow of
Solution: Use Edmond Karp Algo (=Ford Fulkerson with shortest path)
b) Does the maximal flow change if edge is capped.
Solution: No, same flow can be pushed over other edges if (a,d) is missing
4 Irreducible Polynoms / System of Congruences[Bearbeiten | Quelltext bearbeiten]
Irreducible Polynoms over Z3[Bearbeiten | Quelltext bearbeiten]
Solution: Plug in all , irreducible if there are no roots
System of Congruences[Bearbeiten | Quelltext bearbeiten]
Solution: Fermat's little theorem for the y^3 part, then Chinese Remainder Theorem