TU Wien:Diskrete Mathematik für Informatik VO (Drmota)/Prüfung 2017-03-03
Zur Navigation springen
Zur Suche springen
1 Erzeugende Funktionen[Bearbeiten | Quelltext bearbeiten]
a) A(z) ist bekannt, bestimme die erzeugende Funktionen für und
b) erzeugende Funktionen D(z) für :
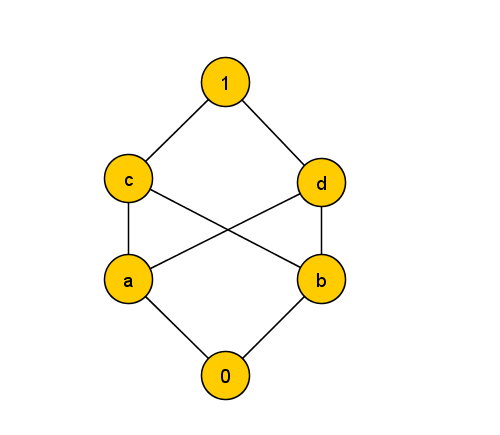
2 Möbiusfunction[Bearbeiten | Quelltext bearbeiten]
a) Calculate Möbiusfunction
b) Relations (c,b) and (d,a) removed, what is the new
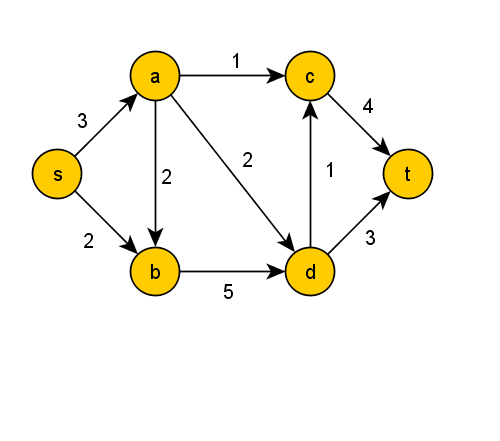
3 Maximal Flow[Bearbeiten | Quelltext bearbeiten]
a) Maximal Flow with Ford-Fulkerson algorithm
b) Does the maximal flow change if edge is capped.
4 System of Congruences[Bearbeiten | Quelltext bearbeiten]
System of Congruences[Bearbeiten | Quelltext bearbeiten]