TU Wien:Diskrete Mathematik für Informatik VU (Drmota)/Übungen WS20/Beispiel 24

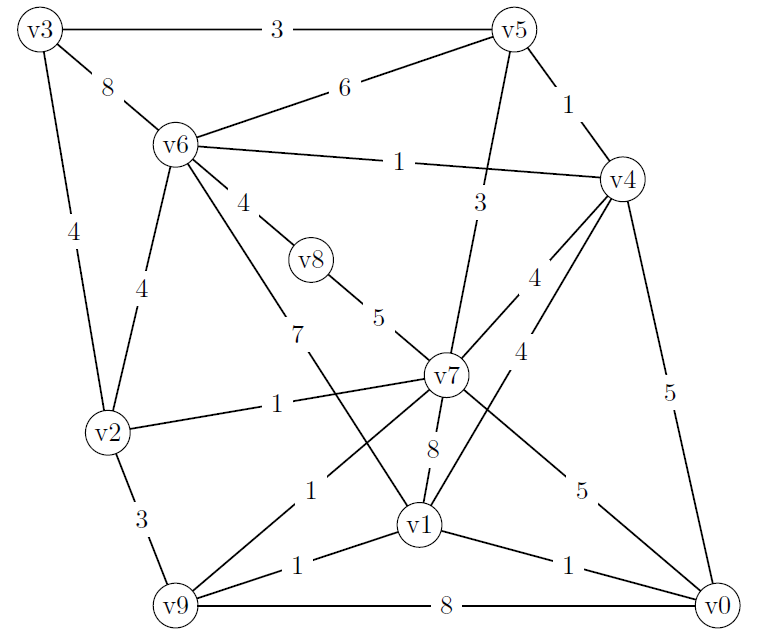
Modify Dijkstra's algorithm such that it finds a path whose longest edge is as short as possible and apply it to the first graph in exercise 16, starting at $v_{0}$.

Dieses Beispiel hat einen unbekannten Lösungsstatus. Bitte editiere diese Seite und schreibe den dir bekannten Status ins Beispiel. Die möglichen Werte sind hier: Vorlage:Beispiel dokumentiert. Führe folgende Änderung durch:

{{Beispiel|1=
Angabetext
}}

oder

{{Beispiel|
Angabetext
}}

zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)

{{Beispiel|status=solved|1=
Angabetext
}}

Graph from exercise 16:

Lösungsvorschlag

Instead of considering the weights for the path until a vertex, consider only the weights of the currently available edges.

Iteration	v0	v1	v2	v3	v4	v5	v6	v7	v8	v9	Auswahl	Vorgänger
0	0	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$	v0
1		1	$\infty$	$\infty$	5	$\infty$	$\infty$	5	$\infty$	8	v1	v0
2			$\infty$	$\infty$	4	$\infty$	7	5	$\infty$	1	v9	v1
3			3	$\infty$	4	$\infty$	7	1	$\infty$		v7	v9
4			1	$\infty$	4	3	7		5		v2	v7
5				4	4	3	4		5		v5	v7
6				3	1		4		5		v4	v5
7				3			1		5		v6	v4
8				3					4		v3	v5
9									4		v8	v6

Materialien

Neues Material hinzufügen

G

• Graph 16.png (details)