TU Wien:Diskrete Mathematik für Informatik VU (Drmota)/Übungen WS20/Beispiel 34

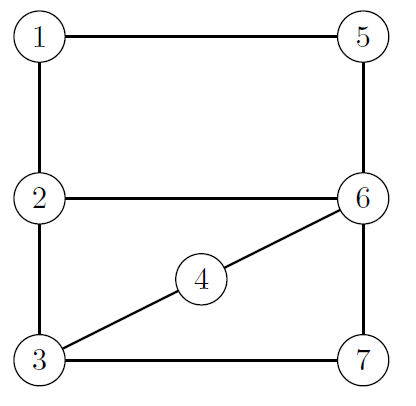
Compute the closure of the following graph:

Dieses Beispiel hat einen unbekannten Lösungsstatus. Bitte editiere diese Seite und schreibe den dir bekannten Status ins Beispiel. Die möglichen Werte sind hier: Vorlage:Beispiel dokumentiert. Führe folgende Änderung durch:

{{Beispiel|1=
Angabetext
}}

oder

{{Beispiel|
Angabetext
}}

zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)

{{Beispiel|status=solved|1=
Angabetext
}}

Lösungsvorschlag

Closure: Given a Graph $G=(V,E),\forall v,w\in V$ with $d(v)+d(w)>=|V|$ add the edge (v,w) to E</math>

Write down all possible edges/vertex pairs (which are not yet part of the graph). Then check the formula above for each of these vertex pairs. If the sum of the degrees is larger than the number of vertices, add the edge, and restart the comparison for those pairs, where one of the vertices has now a higher degree.
Example:

Possible pairs/edges: (v1, v3) (v1, v4) (v1, v6) (v1, v7) (v2, v4) (v2, v5) (v2, v7) (v3, v5) (v3, v6) (v4, v5) (v4, v7) (v5, v7)
Check edges, e.g. for (v3, v6) the formula holds --> add the edge to the graph
Possible pairs/edges: (v1, v3) (v1, v4) (v1, v6) (v1, v7) (v2, v4) (v2, v5) (v2, v7) (v3, v5) (v3, v6) (v4, v5) (v4, v7) (v5, v7)
Check edges (recheck pairs where one of the vertices is v3 or v6): (v1, v6) --> add the edge to the graph
etc....

Materialien

Neues Material hinzufügen

A

• Angabe.png (details)