TU Wien:Einführung in Visual Computing VU (W. Kropatsch, W. Purgathofer, R. Sablatnig)/Zusammenfassung Test 1
Für den Stoff der zum 2. Test hinzukommt, siehe hier.
Computergraphik[Bearbeiten | Quelltext bearbeiten]
Teilgebiet der Informatik, das sich mit künstlich erzeugten Bildern und deren Manipulation beschäftigt.
Zu den Anwendungsgebieten zählen Entertainment, Computer Aided Design (CAD), Werbung, Simulatoren, Kulturerbe und die Wissenschaft.
Graphikpipeline, Objektrepräsentation[Bearbeiten | Quelltext bearbeiten]
Informationen werden in aufeinanderfolgenden Schritten in ein Bild transformiert.
Viewing-Pipeline Objektkoordinaten ↓ Modelltransformation Weltkoordinaten ↓ View-Transformation Kamerakoordinaten ↓ Projektion + Homogenisierung normalisierte Gerätekoordinaten ↓ Viewport-Transformation Pixelkoordinaten
Rendering-Pipeline Objektkoordinaten ↓ Objekterschaffung Objekte im Objektraum ↓ Modellierung ↓ Viewing ↓ Projektion transformierte Punkte im Clipraum ↓ Clipping + Homogenisierung Szene in normalisierten Gerätekoord. ↓ Viewport-Transformation ↓ Rasterisierung ↓ Schattierung Rasterbild in Pixelkoordinaten
- Polygon-Listen
- Boundary-Representation (B-Rep)
- Eine Menge von Polygonen, die die Oberfläche eines Objektes beschreibt.
- Punkt (Vertex), Kante, Fläche
- Constructive Solid Geometry (CSG)
- Quadtrees und Octrees
- Szenengraphen
Geometrische Transformationen[Bearbeiten | Quelltext bearbeiten]
2D-Transformationen[Bearbeiten | Quelltext bearbeiten]
Normalerweise skaliert man, dann rotiert man, dann translatiert man (T * R * S).
- Translation
- Rotation
- (gegen Uhrzeigersinn)
- Skalierung
- Reflexion: Skalierung mit -1
- Homogene Koordinaten
3D-Transformationen[Bearbeiten | Quelltext bearbeiten]
z.B. Spiegelung um yz-Ebene:
Farbe[Bearbeiten | Quelltext bearbeiten]
- Kolorimetrie
- Wissenschaft von der technischen Beschreibung von Farben
- Farbfehlsichtigkeit
- Farbmodelle
- CIE 1931 XYZ-Farbmodell
- RGB-Farbmodell: Rot, Grün, Blau (additiv)
- CMY-Farbmodell: Cyan, Magenta, Yellow (subtraktiv), CMYK
- HSV-Farbraum: Farbton, Sättigung, Helligkeit (hue, saturation, value), HLS
- Farbsymbolik
Rasterisierung[Bearbeiten | Quelltext bearbeiten]
- Linienalgorithmen
- Attribute
- Baryzentrische Koordinaten
- Punkt wird als gewichtetes Mittel der Eckpunkte des Dreiecks dargestellt:
- Ein Punkt liegt im Dreieck, wenn α, β und γ zwischen 0 und 1 liegen.
Was ist bei einem Polygon innen?[Bearbeiten | Quelltext bearbeiten]
- Odd-Even-Rule
- Zieht man von einem Punkt aus einen beliebigen Halbstrahl, so ist der Punkt innerhalb, wenn die Zahl der Schnitte mit der Kurve ungerade ist, ansonsten ist der Punkt außerhalb.
- Nonzero-Winding-Number-Rule
- Punkte sind außerhalb, wenn sich auf einem beliebigen Halbstrahl gleich viele im Uhrzeigersinn und gegen den Uhrzeigersinn verlaufende Kurvenkanten befinden, ansonsten innerhalb.
- All-In-Rule
- Alles, was irgendwie umschlossen ist, ist innen. (selten verwendet)
Ein Polygon heißt konvex wenn alle inneren Winkel kleiner als 180° sind, andernfalls konkav.
Polygonfüllen[Bearbeiten | Quelltext bearbeiten]
- Scanlinien-Flächenfüllen
- Floodfill-Algorithmus
- Paralleles Füllen konvexer Polygone
- Behandlung von 3D Polygonen
Viewing[Bearbeiten | Quelltext bearbeiten]
- Viewport-Transformation
- Projektionstransformation
- Kamera-Transformation
- Orthographisches Viewing
- Perspektive
Computer Vision[Bearbeiten | Quelltext bearbeiten]
Zu den Anwendungsgebieten zählen Kontrollprozesse, Navigation, Erkennen von Ereignissen, Informationsorganisation, Modellierung von Objekten und Umgebungen, und Interaktion.
- Plenoptische Funktion berechnet die Lichtintensität aus mehreren Eingabeparametern
- Camera Obscura / Lochkamera
Bildaufnahme[Bearbeiten | Quelltext bearbeiten]
- Das menschliche Auge
- Perspektivische Projektion
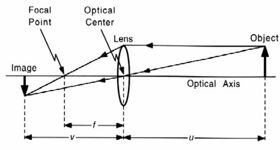
- einfache Linsengleichung
- Radiometrie
- Methoden zur Messung elektromagnetischer Strahlung
- Sampling
- radiometrische Auflösung
- Anzahl der unterscheidbaren Grautonstufen
- Bildsensoren
- Farbe auf CCD Sensoren
- Field Sequential Technik
- Color Filter Array (CFA), z.B. Bayer Filter
Der Mensch ist für grünes Licht am empfindlichsten.
- Ideale vs. Reale Kamera
- optische Aberration
- chromatische Aberration
- sphärische Aberration
- Linsen-Verzerrung
- Weißabgleich
Bildcodierung und Kompression[Bearbeiten | Quelltext bearbeiten]
- Digitales Bild-Dateiformat
- Raster-Bildformate
- Vektor-Bildformate
- Bildkompression
- Verlustfreie Kompression
- Lauflängenkodierung (Run Length Encoding; RLE)
- Huffman-Codierung
- Lempel Ziv (LZ)
- Bildformate, die verlustfreie Kompression verwenden (z.B. GIF, PNG und TIFF)
- Verlustbehaftete Kompression
- JPEG
- Farbraumkonversion und Downsampling
- Kosinustransformation und Quantisierung im Spektralraum
- verlustfreie Kompression
- JPEG
- Diskrete Cosinus Transformation (DCT)
- Verlustfreie Kompression
- Video Kompression
- Interframe-Kompression
- Intraframe-Kompression
- MPEG (Moving Picture Experts Group)
Punktoperationen[Bearbeiten | Quelltext bearbeiten]
Punktoperationen berücksichtigen nur den aktuellen Pixel und keine Nachbarpixel. Punktoperationen, welche keine Bildkoordinaten berücksichtigen heißen homogen (andernfalls inhomogen).
- Identitätsfunktion und Invertierung
- Schwellwertoperation
- Kontrast und Helligkeit
- Histogramm
- Histogrammnormalisierung
- Histogrammequalisierung
Lokale Operationen[Bearbeiten | Quelltext bearbeiten]
Auch Filteroperationen (kurz Filter) genannt. Ergebnis wird aus mehreren Pixeln (einer zusammenhängenden Region) berechnet. Geometrie des Bildes bleibt erhalten.
- Nachbarschaften
Lineare Filter[Bearbeiten | Quelltext bearbeiten]
- Tiefpassfilter (z.B. Mittelwertfilter und Gauß-Filter)
- Hochpassfilter
- Differenzfilter
- basierend auf 1. Ableitung: Gradientenfilter
- basierend auf 2. Ableitung: Laplace-Filter
- Differenzfilter
- Bildrandproblem
- Formale Eigenschaften linearer Filter
- Faltungsoperation
- kommutativ, linear, assoziativ
- Separierbarkeit
Nicht-lineare Filter[Bearbeiten | Quelltext bearbeiten]
- Minimumfilter
- Medianfilter: Median der sortierten Werte; gut für Salt und Pepper Noise
- Maximumfilter
Kanten Filterung[Bearbeiten | Quelltext bearbeiten]
- Bildschärfung
- Laplace-Operator
- Kanten
- Gradienten-basierte Kantendetektion
- Kantendetektionsfilter
- Prewitt-Operator
- Sobel-Operator
- Roberts-Operator
- Kirsch-Operator
- Kantendetektion mit zweiten Ableitungen
- Laplace-Operator
- Laplacian-of-Gaussian-Operator (LoG)
- Canny Operator
Globale Operationen[Bearbeiten | Quelltext bearbeiten]
Globale Operationen verwenden das gesamte Bild als Ausgangsbasis.