TU Wien:Einführung in die Technische Informatik VO (Schildt)/Ausarbeitung praktische Prüfungsbeispiele WS10

Hier ensteht der Versuch einer gesammelten Ausarbeitung der Praktischen Prüfungsbeispiele zu ETI

Schaltalgebra

Kühlschrank

Angabe

Der Alarm eines Kühlschranks soll anschlagen, wenn der Temperatursensor über 12°C misst. Die Temperatur wird vom Sensor ganzzahlig von 0°C bis 15°C in 4 Bit-Darstellung geliefert

• a) Tragen Sie entsprechende Werte in unten stehende Wahrheitstabelle ein.
• b) Wie lautet die minimale Boolsche Funktion y, die den Alarm ansteuert, also logisch "1" ausgibt, wenn die Temperatur 12°C überschreitet.
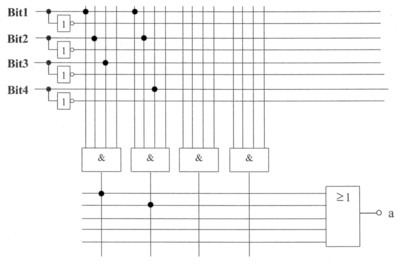
• c) Skizzieren Sie die Funktion y in untestehendem PLA
• d) Berechnen Sie die maximale Taktfrequenz der PLA-Schaltung aus c) unter der Annahme, dass eine Negation 10ns und ein Gatter 20ns Durchlaufzeit hat.

Lösungsvorschlag

Wahrheitstabelle:

b1	b2	b3	b4	> 12°
0	0	0	0	0
0	0	0	1	0
0	0	1	0	0
0	0	1	1	0
0	1	0	0	0
0	1	0	1	0
0	1	1	0	0
0	1	1	1	0
1	0	0	0	0
1	0	0	1	0
1	0	1	0	0
1	0	1	1	0
1	1	0	0	0
1	1	0	1	1
1	1	1	0	1
1	1	1	1	1

Funktion y:

${\begin{aligned}y&=(b_{1}\land b_{2}\land \neg b_{3}\land b_{4})\lor (b_{1}\land b_{2}\land b_{3}\land \neg b_{4})\lor (b_{1}\land b_{2}\land b_{3}\land b_{4})\\&=(b_{1}\land b_{2}\land b_{3})\lor (b_{1}\land b_{2}\land b_{4})\end{aligned}}$

${\begin{aligned}y&=(b_{1}\land b_{2})\land (b_{3}\lor b_{4})\end{aligned}}$

PLA

(praktisch die erste zeile aus y hier nach der reihe eingetragen)

Maximale Takfrequenz

$f_{max}={\frac {1}{t_{min}}}$, $t_{min}\,$ ist dabei die zeit, die man mindestens braucht um einmal durch das komplette schaltnetz zu laufen. (minmale taktperiode)

also, wir müssen mindestens 2 gatter durchlaufen (AND und OR) (werte aus der angabe lesen):

$t_{min}=2*20ns=40ns\,$

$f_{max}={\frac {1}{40ns}}=0.025$

was 25MHz entspricht.

--thomas 16:58, 7. Okt. 2010 (CEST)

Haushalt - Geräte

Angabe

In einem Haushalt befinden sich folgende Geräte: Spülmaschine (S) mit 2200W, Waschmaschine (W) mit 2200W, Trockner (T) mit 1350W, Elektro-Kochmulde (E) mit 3500W und eine Kaffeemaschine (K) mit 1300W.
Ein Alarm soll anschlagen, wenn die Gesamtleistung 5000W überschreitet. Zur Ansteuerung des Alarms erhalten Sie von den Geräten Signale mit folgender Bedeutung: "0" bedeutet, dass das Gerät nicht in Betrieb ist, "1" beduetet, dass das Gerät läuft.
Tip: Sie können Quine-McCluskey als Minimierungsverfahren verwenden, müssen es aber nicht!

• a) Tragen Sie entsprechende Werte in unten stehende Wahrheitstabelle ein.
• b) Wie lautet die minimale Boolsche Funktion y, die den Alarm ansteuert, also logisch "1" ausgibt, wenn die Gesamtleistung 5000W überschreitet?
• c) Skizzieren Sie die Ausgangsfunktion in untenstehendem PLA
• d) Berechnen Sie die maximale Taktfrequenz der PLA-Schaltung aus c) unter der Annahme, dass eine Negation 10ns und ein Gatter 20ns Durchlaufzeit hat.

Lösungsvorschlag

Wahrheitstabelle:

E	S	W	T	K	> 5000W
0	0	0	0	0	0
0	0	0	0	1	0
0	0	0	1	0	0
0	0	0	1	1	0
0	0	1	0	0	0
0	0	1	0	1	0
0	0	1	1	0	0
0	0	1	1	1	0
0	1	0	0	0	0
0	1	0	0	1	0
0	1	0	1	0	0
0	1	0	1	1	0
0	1	1	0	0	0
0	1	1	0	1	1
0	1	1	1	0	1
0	1	1	1	1	1
1	0	0	0	0	0
1	0	0	0	1	0
1	0	0	1	0	0
1	0	0	1	1	1
1	0	1	0	0	1
1	0	1	0	1	1
1	0	1	1	0	1
1	0	1	1	1	1
1	1	0	0	0	1
1	1	0	0	1	1
1	1	0	1	0	1
1	1	0	1	1	1
1	1	1	0	0	1
1	1	1	0	1	1
1	1	1	1	0	1
1	1	1	1	1	1

Funktion y:

Wenn man sich ausrechnet, bei welchen Geräten der Verbrauch über 5000 W steigt, erkennt man schnell, dass gewisse Kombinationen immer über 5000 Watt ergeben, wie E mit S (oder W welches gleich viel verbraucht). Diese offensichtlichen Zusammenhänge kann man einfach direkt als boolsche Formel aufschreiben.

${\begin{aligned}y&=(S\land W\land T)\lor (S\land W\land K)\lor (E\land W)\lor (E\land S)\lor (E\land T\land K)\end{aligned}}$

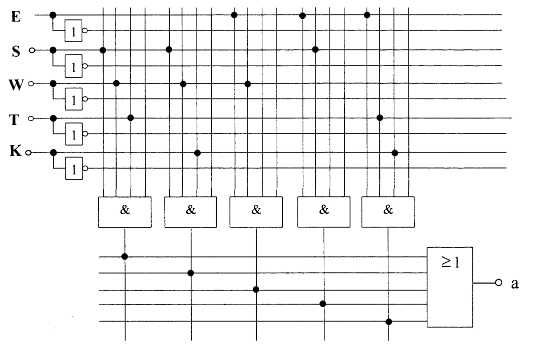
PLA

Die Funktion y wird einfach genau wie oben auf dem PLA markiert.

Maximale Takfrequenz

$t_{min}=2*20ns=40ns=40*10^{-9}\,$

$f_{max}={\frac {1}{40*10^{-9}}}=25000000=25MHz$
edit: eine 0 hat gefehlt ..

Schaltwerke

Bombe

Angabe

Sie sind diensthabender Informatiker in der nationalen Anti-Terror Organisation und als Experte zum Bombenkommando hinzugezogen worden. Vor Ort finden Sie ein Schaltwerk vor, das nur über einen Eingang E verfügt. Zusätzlich findet die Spurensicherung folgende Skizze:

• a) Wie wird der Terrorist die Ausgänge beschalten, um den Zünder der Bombe anzusteuern? (Geben sie die logische Schaltung an)
• b) Welche Bitfolge legt der Terrorist an, um die Bombe zu entschärfen?
• c) Welche Bitfolge legen Sie an, wenn Sie nicht wissen, in welchem Zustand sich das Schaltwerk befindet und die Bombe weder gezündet noch entschärft wurde? Ihr Ziel ist es, den Startzustand Armed zu erreichen.
• d) Um welche Art von Schaltwerk handelt es sich hier, und warum?
• e) Welche Art der Zustandscodierung wurde verwendet?
• f) Welche formalen Fehler sind dem Terroristen im Entwurf des Zustandsgraphen unterlaufen?

Lösungsvorschlag

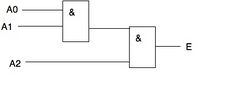
a) A0 = 1, A1 = 1, A2 = 1

b) Aus "Armed" -> 1111

c) Überlegung (Beispielkonkret): sieht man sich die eingabewerte an, führen wegen, wenn man lauter 0 eingibt, von allen zuständen entweder nach "Armed", oder nach "Minsk". beide zustände sind fallen für 0 eingaben. dh wenn wir lauter nullen anlegen, kommen wir auf jeden fall (egal wo wir stehen) entweder nach "Minsk" oder nach "Armed". von beiden zuständen aus, kommt man mit 1 auf jeden fall nach "Rome", und von dort mit 110 auf jedenfall nach "Armed".

wieviele nullen man vorher reinklopft ist im prinzip egal, sieht man sich den graphen etwas an, sieht man, dass 3 nullen reichen um auf jeden fall nach "Minsk" oder nach "Armed" zu kommen.

lösung ist also: 000 (von überall nach "Minsk"/"Armed") + 1 (nach "Rome") + 110 (nach "Armed") => 0001110

d) Mealey Schaltwerk.

Da die Ausgänge beim Mealy-Schaltwerk von den Eingängen abhängen, sind sie im Graphen nicht mehr den Zuständen, sondern den Zustandsübergängen zugeordnet, die ja ebenfalls von den Eingängen abhängen.

e) Dichte Zustandscodierung. Man sieht 3 Bits für 8 Zustände.

f) Der Zustandsgraph ist nicht widerspruchsfrei.

Der Übergang von Minsk zeigt X auf Minks, was Minsk zu einer Falle für alle weiteren Eingaben machen würde. Allerdings hat Minsk mit Eingabe 0 einen Folgezustand. Richtig wäre also statt X, 1. Jedes Eingangsbitmuster darf immer nur auf einer von einem Zustand wegführenden Kante notiert sein.

--thomas 17:48, 7. Okt. 2010 (CEST)

Garagentor

Angabe

Entwerfen Sie eine möglichst einfache State Machine für die Ansteuerung eines Motors, der ein Garagentor bewegen soll.
Als Eingangssignale der Schaltung stehen zwei Endschalter ($S_{o}$, $S_{u}$) zur Verfügung, die logisch 1 werden, sobald das Tor die enstrepchende Endposition erreicht hat ($S_{o}$ für oben und $S_{u}$ für unten). Außerdem gibt es einen Taster (E), mit dem das Tor in Bewegung versetzt werden soll. Die Ausgänge $A_{0}$ und $A_{1}$ bewegen den Motor in die entsprechende Richtung. Realisieren sie die Aufgabe als Moore-Schaltwerk mit 1-aus-n Codierung. Die gewünschten Zustände, sowie die Kantenbezeichnung des Graphen sind ebenfalls vorgegeben.

• a) Entwerfen Sie den Zustandsgraphen
• b) Skizzieren Sie die allgemeine Schaltung (mit Übergangsfunktion und D-Latches zur Zustandsspeicherung)
• c) Stellen Sie die Tabelle für die Übergangsfunktion auf

Semaphor

-- todo