TU Wien:Einführung in die Telekommunikation VO (Goiser)/Ausarbeitung häufiger Prüfungsfragen SS10

Ausarbeitung von Fragen die laut Informatik-Forum und Prüfungsberichten im VOWI bei Prüfungen häufig vorgekommen sind. Stellen mit TODO sind noch auszuarbeiten - deine Hilfe ist gefragt!

Quellen:

• Folien vom SS2010
• Ausarbeitung von Matthias Neugschwandtner und Matthias Auchmann

Einleitung

Generisches Modell

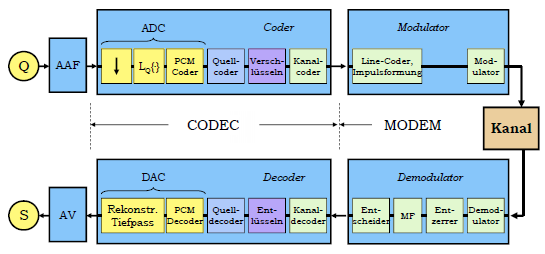
Quelle -> AAF -> +---------+ -> +----------+ ->
                 |  CODEC  |    |   MODEM  |    Kanal
Senke  <- AV  <- +---------+ <- +----------+ <-

Quelle -> Anti-Aliasing-Filter -> Coder-Teil von CODEC   -> Modulator-Teil von MODEM   ->
                                                                                          Kanal
Senke  <- Audio-Verstärker     <- Decoder-Teil von CODEC <- Demodulator-Teil von MODEM <-

• Coder besteht aus:
  • ADC:
    • Abtastung ($\Rightarrow$ PAM)
    • Quantisierung der abgetasteten Werte ($\Rightarrow$ "quantisierte" PAM)
    • Zahl, welche eindeutig die Quantisierungsstufe (Amplitude) darstellt, binär codieren ($\Rightarrow$ PCM)
  • Quellkodierung: Entfernung von Redundanz
  • Verschlüsselung
  • Kanalkodierung: Gezieltes Hinzufügen von Redundanz

• Modulator besteht aus:
  • Line-Coder, Impulsformung
    • erzeugt aus dem Bitstrom ein Basisbandsignal
    • Wichtig die Frage: "Wie formt man Impulse, sodass sie nahe der maximalen Symbolrate (Nyquist: 2*B Symbole/s) übertragen werden können?"
  • Modulator
    • Ziel: Frequenzumsetzung und Filterung auf Übertragungsbandbreite
    • erzeugt aus Basisbandsignal ein Bandpasssignal (durch Multiplikation mit einem Trägersignal)

• Demodulator besteht aus:
  • Demodulator
    • Bandpasssignal $\rightarrow$ Basisbandsignal
  • Entzerrer
  • Matched Filter (MF): maximiert SNR vor der Entscheidungsstufe
  • Entscheider

• Decoder besteht aus:
  • Kanaldecoder
  • Entschlüsseln
  • Quelldecoder
  • DAC:
    • PCM Decoder
    • Rekonstruktion Tiefpass

Warum digitale Kommunikationssysteme?

• Einfache Informationsdarstellung durch Bits
• Einfache Speicherung
• Einfache Informationsverarbeitung (Quellkodierung, Komprimierung, Verschlüsselung, Kanalkodierung)
• Einfache Signalverarbeitung (Abtasten, Quantisieren)
• Robust gegen Amplitudenstörungen

Signale und Systeme

Energiedichtespektrum

• Leistungsdichtespektrum eines periodischen Signals: $G_{1}(f)={\frac {|V(f)|^{2}}{\sqrt {2}}}$
• Energiedichtespektrum eines transienten Signals: $\ G_{2}(f)=|V(f)|^{2}$

Edit Ford_Prefect:

• Leistungsdichtespektrum eines periodischen Signals: $G(f)={\frac {|S_{RMS}(f)|^{2}}{R}}={\frac {|S(f)|^{2}}{2R}}$
• Energiedichtespektrum analog

Leistungsdichtespektrum von periodischen Signalen ist diskret, Energiedichtespektrum ist immer kontinuierlich.

Autokorrelationsfunktion

Betrachtet man das Skalarprodukt eines Signals mit sich selbst, so bekommt man die Autokorrelationsfunktion $\Rightarrow$ die Autokorrelationsfunktion gibt die Ähnlichkeit eines Signals mit einer zeitversetzten Kopie seiner selbst an

Eigenschaften:

• Autokorrelationsfunktion ist gerade
• Maximumstelle der Autokorrelationsfunktion in 0

Wiener-Kintchin Theorem

[Wikipedia-Definition: Besagt, dass die spektrale Leistungsdichte eines "stationären Zufallsprozesses" die Fourier-Transformation der korrespondierenden Autokorrelationsfunktionen ist.]

Die Autokorrelationsfunktion und das doppelseitige Leistungsdichtespektrum von $x(t)$ bilden eine Fouriertransformations-Paar:

$R_{x}(\tau )\Longleftrightarrow ^{FT}G_{x}(f)$

$\ R_{x}(\tau )$ ... Autokorrelationsfunktion

$\ G_{x}(f)$ ... Spektrale Leistungsdichte

bzw. FT ausgeschrieben: $G_{x}(f)=\int _{-\infty }^{\infty }R_{x}(\tau )e^{-j\pi 2f\tau }d\tau$

Zufallssignale und AWGN

TODO

Zufallssignale sind Signale, deren Verlauf sich nicht durch mittels einer Funktion darstellen lässt. Sie können lediglich mit Werkzeugen der Wahrscheinlichkeitsrechnung beschrieben werden.

AWGN = (Additive White Gaussian Noise).

Es ist ein Rauschen das Aufgrund der Physikalischen Kanaleigenschaften auftritt. Dieses Rauschen hat über die Kanalbandbreite eine konstante spektrale Rauschleistungsdichte und wird zum Signal dazu addiert, daher der Name Additiv. Die Signalamplituden des Rauschen sind Gaußverteilt(Gaußglocke) und die Spannungen sind unkorreliert.

[1] AWGN Wikipedia

Zentraler Grenzwertsatz

Addiert man zwei Zufallsvariablen (d.h. $X+Y=Z$), so stellt sich die Frage wie die aus dieser Addition hervorgehende Dichte $p_{z}(z)$ aussieht. [TODO Formeln]

Die Dichtefunktion der resultierenden Zufallsvaraiblen $Z$ ergibt sich durch Faltung der Dichtefunktionen von $X$ und $Y$.

Addiert man N stochastich unabhängige Zufallsvariablen, so hat die Summe eine Dichtefunktion, die sich mit $N\rightarrow \infty$ der Gauß'schen Glockenkurve annähert.

Die Verteilung der Summe ist also für $N\rightarrow \infty$ normalverteilt.

Definition von den Folien:

• Die WDF einer Summe von N statistisch unabhängigen Zufallsvariablen nähert sich der Gauß'schen WDF unabhängig davon welche WDF die einzelnen Summanden haben.

Rayleigh und Rice Verteilung

Bei nichtlinearen Systemen: X, Y sind statistisch unabhängige Gaussvariablen. X^2 und Y^2 gehorchen dann einer Chi-Quadrat Verteilung mit einem Freiheitsgrad. X^2 + Y^2 entspricht dann einer Chi-Quadrat Verteilung mit zwei Freiheitsgraden. sqrt(X^2 + Y^2) ist dann Rayleigh bzw. Rice verteilt - jenachdem ob sie Mittelwertbehaftet (Rice) oder nicht (Rayleigh) sind.

Wird beim Quadraturempfänger (I und Q) benötigt, siehe Foliensatz 2 Seite 203. Es wird auch bei schnellem Schwund im Mobilfunk verwendet.

Stationäre und Ergodische Zufallsprozesse

Stationärer Zufallsprozess

• im engeren Sinne:
  • Die statistischen Parameter sind unabhängig von der Zeit. Alle WDF's (Gemeinsame, Bedingte, Grenz) sind gleich.
• im weitesten Sinne:
  • Mittelwert muss zeitunabhängig sein
  • Korrelation hängt nur von der Zeitdifferenz ($T=t_{2}-t_{1}$) ab

Ergodischer Zufallsprozess

• Scharmittelwert = Zeitmittelwert

Ergodischer Gaußscher Zufallsprozess

• im engeren Sinne:
  • Man benötigt nur eine Musterfunktion. Aus dieser bildet man die zweidimensionale Statistik derart, indem man jeweils 2 Werte, welche konstanten Zeitabstand T zueinander haben, zusammenfasst
• im weitesten Sinne:
  • Wenn Gaußverteilte Zufallszahlen wilkürlich zu einem Zeitsignal zusammengesetzt werden. Die Umkehrung ist auch möglich.

Pulse-Code Modulation (PCM)

Abtasttheorem

"Nyquist-Theorem" bzw. "Shannon'sches Abtasttheorem"

• Hat ein Signal keine Spektralkomponenten oberhalb einer Frequenz $f_{H}$, so kann es nach einer Abtastung in der Theorie dann rekonstruiert werden, wenn die Abtastfrequenz $f_{S}$ mindestens doppelt soch wie $f_{H}$ ist
  • $f_{S}\geq 2\cdot f_{H}$
  • $2\cdot f_{H}$ ... "Nyquist-Frequenz"
  • wenn $f_{S}>2\cdot f_{H}$ ... "Oversampling"
  • wenn $f_{S}<2\cdot f_{H}$ ... "Undersampling"

In der Praxis muss Theorem etwas modifiziert werden, da ein Anti-Aliasing Filter keine unendlich steilen Flanken hat:

• $f_{S}\geq 2.2\cdot f_{H}$ (reales Abtasten)

Gütemaß für den Aliasing-Effekt

Signal/Verzerrungs-Leistungsverhältnis $SDR={\frac {P_{un}}{P_{al}}}$

$P_{un}\$ ... Signalleistung ohne Aliasing

$P_{al}\$ ... Signalleistung mit Aliasing

PCM (Eigenschaften, Quantisierungsrauschen, Companded PCM, Rechenbeispiel)

Quantisierungsrauschen bei quantisierter PAM

Quantisieren ist mit Qualitätsverlust verbunden, da das quantisierte Signal nicht mehr dem Originalsignal entspricht. Der Unterschied zwischen dem letzteren ergibt ein neues Zufallssignal, das Quantisierungsrauschen.

• Maß für das Quantisierungsrauschen: $SNQR$ (signal to quantization noise ratio)

• $SNQR_{max}$ = maximal auftretender Wert von SNR (Verhältnis der maximalen Signalleistung (Aussteuerungsgrenze) zu Quantisierungsrauschleistung)

Bei linearer Quantisierung und einem Signal ohne Gleichanteil mit Gleichverteilung berechnet man SNQR folgendermaßen (M = Anzahl der Quantisierungsstufen):

$SNQR=M^{2}-1\$

$SNQR_{dB}=20\cdot log_{10}(M)dB$

$SNQR_{max}=3M^{2}\$

$SNQR_{max,dB}=4.8+SNQR_{dB}\$

Pulse-Code Modulation

Nachdem PAM-Signal quantisiert wurde, kann man anstatt der Pulse selbst lediglich Nummern, die die Höhe der Pulse angeben, übertragen ($\Rightarrow$ PCM). Bei M Amplitudenwerten ist das Codewort $n=\lceil ld(M)\rceil Bit$ lang.

SNQR hängt nicht von der Kodierung ab und bleibt daher gleich, als Funktion von n:

$SNQR=(2^{n})^{2}-1\$

$SNQR_{max}=3\cdot (2^{n})^{2}$

Schätzwert für SNQR $\rightarrow$ $6\cdot (n-1)dB$

• Nachteil von PCM:
  • benötigt mehr Bandbreite als natives PAM-Signal, da mehr Pulse statt einem übertragen werden
• Vorteil von PCM:
  • jedoch können Spannungslevel bei PCM weitaus leichter unterschieden werden als bei PAM (es kommt nur auf das Vorzeichen an), PCM ist also weniger anfällig auf Rauschen

Der Bandbreitenbedarf nimmt weniger stark zu, wenn die Anzahl der Quantisierungsstufen erhöht wird, als wenn das SNR erhöht wird:

$SNR\propto M^{2}$

$R_{b}\propto ld(M)$

Companded PCM

Bei gewöhnlichen Signalen kann nicht davon ausgegangen werden, dass alle Quantisierungslevel gleichmäßig genutzt werden, d.h. die Dichte des Informationssignals gleichmäßig verteilt ist. Um Quantisierungsrauschen zu minimieren ist es also sinnvoll, die Quantisierungslevel an den häufig genutzten Stellen zu verdichten und an den weniger genutzten Stellen zu erweitern.

$\Rightarrow$ Diese nicht-lineare Quantisierung nennt man Companding (Signal wird mit nicht-linearer Amplitudencharakteristik komprimiert und dann das empfangene Signal mit inverser Charakteristik dekomprimiert)

$\Rightarrow$ Es wird eine nahezu gleichverteilte Amplitudenstatistik erreicht.

Möglichkeiten zur Bandbreitenreduktion

• Delta PCM:
  • statt Abtastwerte selbst wird nur die Differenz zum vorangegangenen Abtastwert übertragen; da Differenz überlicherweise kleiner ist als die tatsächlichen Abtastwerte (da nahe bei einanderliegende Abtastwerte üblicherweise korrelieren), sind kürzere Codewörter nötig
• Differentielles PCM (DPCM):
  • macht sich ebenfalls die Korrelation benachbarter Abtastwerte zunutze und benutzt einen Algorithmus um zukünftige Abtastwerte vorauszusagen
• Adaptives DPCM (ADPCM):
  • Koeffizienten bzw. Gewichte der Vorhersage-Einheit sind nicht fix festgelegt, sondern werden entsprechend der sich ändernden Signalstatistik des Informationssignals angepasst
• Deltamodulation:
  • DPCM-System, wobei Auflösung des Quantisierers auf 1 Bit reduziert wird

Basisbandübertragung und Detektion binärer Symbole in AWGN

TODO Möchte man aus einem übertragenen Signal binäre Symbole auslesen, so muss man zu einem bestimmten Zeitpunkt eine Messung/Abtastung des Signals durchführen und basierend darauf die Entscheidung zischen 0 und 1 treffen. Für diese Entscheidung folgen wir dem Satz von Bayer, welcher etwa lautet: "Wähle jene Hypothese(Signal), welche die größte Wahrscheinlichkeit besitzt."

Zwei Möglichkeiten der Abtastung:

Center Point Detection (CPD), welche die Messung in der Mitte des Symbolschlitzes durchführt

Integrate and Dump, welche mehrere Messungen pro Symbolschlitz durchführt, diese addiert und sich bei überschreiten eines definierten Grenzwertes für ein Symbol entscheidet.

Die Basisbandübertragung kann entweder unipolar (Aussteuerung nur in eine Richtung) oder Bipolar (Aussteuerung in positive und negative Richtung) erfolgen.

Bei gleicher SEP benötigt man bei bipolarer Signalisierung die halbe Leistung als bei unipolarer.

Durch die Übertragung am Kanal kann es zu Verzerrungen des Signals kommen, welche vor der Symtaktrückgewinnung durch ein Filter Entzerrt werden.

Center Point Detection

Abtasten in der Symbolmitte, Symbolentscheidung auf Grund eines verrauschten Samples pro Symbol $\Rightarrow$ es treten oft Polaritäts-Fehler auf.

Entscheidungskette: Kurvenform $\rightarrow$ Numerischer Wert $\rightarrow$ Entscheidung

Optimale Filterung

Optimale Filterung

Wird eingesetzt um folgende Aufgaben zu erfüllen:

• (im Sender) - Impulsformung für optimale Übertragung
  • Ziel: Bandbreite des Kanalsignals zu minimieren
• (im Empfänger) - Filterung für optimale Detektion
  • Ziel: SNR zum Entscheidungszeitpunkt zu maximieren um die Bitfehlerwahrscheinlichkeit zu minimieren
• (im Empfänger) - Filter zur Entzerrung der Kanalimpulsantwort
  • Ziel: Verzerrungen verursacht durch den Kanal rückgängig machen

Intersymbolinterferenz (ISI)

Signalisierung mit Rechteckimpulsen hat theoretisch unendliche Bandbreite und ist deshalb praktisch nicht realisierbar. Wenn man jedoch ein gewisses Maß an Verzerrung in Kauf nimmt, können "Rechteckimpulse" auch über Kanäle mit begrenzter Bandbreite übertragen werden.

Ist die Verzerrung allerdings zu stark, so überlappen sich die Pulse im Zeitbereich und die Spannung zum Abtastzeitpunkt kann nicht nur vom gewünschten, sondern zusätzlich von einem oder mehreren vorigen Pulsen herrühren;

$\Rightarrow$ dieses Verschmieren eines Pulses in einen anderen wird als Intersymbolinterferenz (ISI) bezeichnet

Performance digitaler Kommunikation wird allerdings nur zum Abtast- bzw. Entscheidungszeitpunkt von der ISI beeinträchtigt. Außerhalb des Entscheidungszeitpunktes ist die ISI irrelevant.

Definition ISI-freies Signal (Zeitaussage)

Signal, das zu allen Abtastzeitpunkten bis auf einen Zeitpunkt $t_{n}$ einen Nulldurchgang hat; das n-te Zeichen kann dann zum Zeitpunkt $t_{n}$ abgetastet werden und stört an den anderen Abtastzeitpunkten $t_{j}$ (wobei $j\neq n$) nicht.

• Bedingung mathematisch: $v(t)\cdot \sum _{n=-\infty }^{\infty }\delta (t-nT_{0})=v(0)\delta (t)$

• sinc-Puls erfüllt in idealer Weise die geforderten Bedingungen! jedoch:
  • sinc-Impulse sind physikalisch nicht realisierbar
  • Nebenkeulen der sinc-Impulse nehmen nur langsam ab (mit ${\frac {1}{t}}$)
  • Abhilfe:
    • Beaufschlage sinc-Impulse mit einer Dämpfungsfunktion
      • $\Rightarrow$ Nullstellen bleiben erhalten, aber Nullstellensteilheit nimmt ab

Definition ISI-freies Signal (Zeitaussage)

Signal $v(t)$ hat ein Amplitudenspektrum $V(f)$ mit ungerader Symmetrie bez. $f_{x}$

Definition ISI-freies Signal (Frequenzaussage)

Amplitudenspektrum $V(f)$ eines ISI freien Signals $v(t)$ wiederholt sich periodisch entlang der Frequenzachse mit Periode ${\frac {1}{T_{0}}}$ und deren Summe ist eine Konstante $v(0)\cdot T_{0}$

Nyquist-Filter / Raised Cosine Filter

Nyquist-Filter sind Filter deren Impulsantworten ISI-frei sind (erzeugen also aus polarisiertem Impulsstrom einen ISI-freien Symbolstrom)

Konstruktion: zur Übertragungsfunktion $H(f)$ eines rechteckigen, linearen Tiefpasses(Rechteckfilter) eine bezüglich der Eckfrequenz $f_{x}$ unsymmetrische Übertragungsfunktion addieren $\Rightarrow$ in Impulsantwort bleiben Nullstellen $sinc(2f_{x}t)$ erhalten.

Raised Cosine Filter

Wichtige Untergruppe der Nyquist-Filter

$\Rightarrow$ Roll-Off entspricht einer halben Cosinus-Funktion

Pulsfilterung für optimales Empfangen

Ziel: verlässlichere Entscheidungen treffen zu können als bei der Center Point Detection; durch Mehrheitsentscheidungen sind Einzelfehler korrigierbar (oder, andere Möglichkeit: n Abtastwerte summieren und mit dem n-fachen des Schwellwerts vergleichen)

Erweitert man die Mehrheitsentscheidung (diskret) auf unendlich viele Entscheidungsvariablen, so gelangt man zur Integration (analog) über die Symboldauer $T_{0}$ (Entscheidungsintervall)

"Integrate and Dump Detector (I&D)"

I&D-Detektor gehört zu den Matched Filter Detektoren

Vorteil: Integrier-Schaltungen mit nachfolgendem Vergleich sind leicht in Hardware zu implementieren (Kondensator und Komparator)

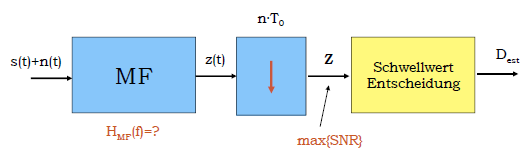
Matched Filter (wozu wird er verwendet, Übertragungsfunktion aufschreiben)

Dient dazu, das SNR vor der Entscheidungsstufe zu maximieren

MF statt CPD einzusetzen bringt eine Einsparung an Sendeleistung bei gleich bleibender BEP (Abhängig vom Zeit/Bandbreite-Produkt).

Um aber die Übertragungsfunktion des MF bestimmen zu können, benötigt man eine geeignete Beschreibung der beteiligten Signale, welche es gestattet das SNR zu erkennen

Amplitudenantwort des MF

Betrachtet man Energiedichtespektrum eines Pulses verglichen mit dem Leistungsdichtespektrum weißen Rauschens (eine konstante Linie), so sieht man, dass manche Frequenzbänder des Pulses einen hohen und manche einen niedrigen Signalrauschabstand haben. Die Frequenzbänder mit hohem SNR sollten einen höheren Einfluss im Entscheidungsprozess haben, als diese mit niedrigem SNR.

$\Rightarrow$ Dieser Umstand führt auf Bilden einer gewichteten Summe der einzelnen Frequenzband Rausch- und Signalenergien, wobei die Gewichte direkt proportional zum SNR des jeweiligen Frequenzbandes sind

• Leistungsdichtespektrum des Rauschens ist konstant, also SNR proportional zu $|V(f)|^{2}$
• Leistung bzw. Energie, die von Filter weitergegeben wird, muss proportional zu $|H(f)|^{2}$ sein

$\Rightarrow$ Quadrat der Amplitudenantwort eines MF muss formgleich zum Energiedichtespektrum des Pulses sein, also $|H(f)|^{2}=k^{2}|V(f)|^{2}\$ (Betragsbedingung) für eine Konstante k

Phasenantwort des MF

• MF zerlegt das Eingangssignal in seine spektralen Komponenten und ordnet diese so um, dass zum Entscheidungszeitpunkt ein Maximum auftritt (konstruktive Überlagerung)

• Konstruktive Überlagerung tritt dann auf, wenn die Phasen des Eingangssignals negiert werden (Nullphasenspektrum)

• Damit das Filter kausal wird, muss noch die Verarbeitungszeit eines Symbols investiert werden, bis das Ergebnis feststeht (lineare Phase)

$\phi (f)=-\phi _{v}(f)-2\pi fT_{0}\$ (Phasenbedingung)

Übertragungsfunktion des MF (ergibt sich aus den beiden Bedingungen)

$H(f)=k\cdot {\underline {V}}^{*}(f)\cdot e^{-j\omega T_{0}}$

Impulsantwort des MF

Frequenzantwort (also Übertragungsfunktion $H(f)$) invers Fourier transformieren:

$h(t)=kv^{*}(T_{0}-t)\$

$\Rightarrow$ d.h. Impulsantwort eines Matched Filter ist die zeitumgekehrte Version des erwarteten Pulses, die zusätzlich um die Pulsdauer verzögert ist ($\rightarrow$ muss sie auch, sonst wäre Filter nicht kausal)

Ausgangssignal des MF

Ergibt sich durch Faltung der Impulsantwort mit dem Eingangssignal:

$z(t)=h(t)*v(t)\$

(WH: Faltung besteht aus dem Umkehren einer Funktion und der Zeitverschiebung des Resultats multipliziert mit der anderen Funktion, und Faltung ist kommutativ)

• Impulsantwort ist bereits eine umgekehrte Kopie des erwarteten Eingangssignals
• Faltung erfordert noch eine Umkehrung $\rightarrow$ Ausgangssignal ist durch das Integral über das Produkt des Eingangssignals mit umgekehrter Impulsantwort gegeben
• in dem Fall, dass Eingangssignal der erwartete Puls ist, multipliziert man unter dem Integral das Eingangssignal mit sich selbst
• $\Rightarrow$ Ausgangssignal ist für das erwartete Signal also die Autokorrelation des Eingangssignals (bis auf eine multiplikative Konstante und eine Zeitverzögerung $T_{0}$)

Root Raised Cosine Filterung

Vereint die beiden Konzepte Nyquistfilterung (ISI-freie Übertragung in bandbeschränkten Kanälen) und Matched Filter (Maximum an SNR zum Entscheidungszeitpunkt).

Die Übertragungsfunktion des Nyquistfilters wird auf Sende- und Empfangsfilter aufgeteilt.

Quellkodierung

Quellkodierung allgemein

Quellkodierung = Werkzeug, welches die Erkenntnisse aus der Informationstheorie umsetzt um die Effizienz der Informationsübertragung zu erhöhen

• Quellkodierung ändert nicht die Entropie der Quelle, Entropie ist fundmentale Größe der Quelle, ABER Quellkodierung liefert eine höhere Entropie in den Codewörtern als die Entropie der Quellsymbole ist, d.h. Kanal wird dadurch nicht mit Symbolen belastet, welche einen geingeren Informationsgehalt besitzen

• Quellkodierung reduziert die Redundanz der Quelle vor der Übertragung

• Effizienz eines Codes kann gesteigert werden, indem man öfters vorkommenden Symbolen weniger Bits zuordnet als jenen Symbolen welche weniger oft vorkommen, d.h. ein effizienter Code, für die gleiche Information, mit weniger Binärstellen im Mittel
  • Problem für Codewörter unterschiedlicher Länge: sie müssen eindeutig decodierbar sein
    • Eigenschaften:
      • Eindeutige Decodierung: Wenn A durch 0 und B durch 00 repräsentiert wird, lässt sich die Folge 0000 nicht eindeutig dekodieren (ABA, AAAA, BB...?)
      • Fortlaufende Decodierung: kein vollständiges Codewort darf Präfix eines größeren Codeworts sein

• Beispiele für Quellkodierung
  • Morse Alphabet: 'e' kommt am häufigsten vor, deshalb wird e ein "." (kürzestes Symbol) zugeordnet
  • Fax
  • Vocoder beseitigen die Redundanz in unserer Sprache (4 formierende Signalformen, "formants")
  • Stringkodierung

Informationsgehalt

Steht im Bezug zur Wahrscheinlichkeit: je wahrscheinlicher es ist, dass eine gewisse Nachricht übertragen wird, desto niedriger ist deren Informationsgehalt;

Anforderungen:

1. Informationsgehalt sollte immer positive Größe sein
2. Informationsgehalt sollte also mit steigender Nachrichtenwahrscheinlichkeit $P(m)$ abnehmen und für eine Wahrscheinlichkeit von $P(m)=1$ (Grenzfall) 0 betragen
3. Informationsgehalt zweier Nachrichten sollte die Summe des Informationsgehaltes der einzelnen Nachrichten sein ("Additivitätseigenschaft" der Information)

• Wahrscheinlichkeit der gesamten Nachricht $\Rightarrow$ Produkt der Wahrscheinlichkeiten der einzelnen Nachrichten, d.h. Informationsgehalt muss summiert werden, wenn Wahrscheinlichkeiten multipliziert werden
  • diese Anforderungen erfüllt der Logarithmus $\Rightarrow I_{m}=-logP(m)$
    • jede Logarithmusfunktion erfüllt die geforderten Bedingungen, d.h es ist gleichgültig welche man verwendet; üblich ist der ld, weil dafür der Informationsgehalt in "Bit" angegeben werden kann $\Rightarrow I_{m}=-ldP(m)$

Entropie

(allg.: Maß für die Regellosigkeit eines Ereignisses als Ergebnis eines Zufallsexperiments)

Ist die mittlere Information, die ein Symbolalphabet beinhaltet, also der Erwartungswert des Informationsgehaltes eines Alphabetes

• ist die Summe der Informationsgehalte der jeweiligen Symbole, jeweils multipliziert mit der Auftrittswahrscheinlichkeit

• ist bei einem Alphabet der Größe 2 (binäre Quelle), und unter der Annahme, dass alle Symbole statistisch unabhängig sind: $H=-\sum _{m=1}^{2}P(m)\cdot log_{2}P(m)$

• Entropie erreicht ihr Maximum wenn alle Symbole gleichwahrscheinlich sind (bei einer binären Quelle also $p={\frac {1}{2}}$, "Faire Quelle")

• hat irgendeine Nachricht eine Wahrscheinlichkeit von 1, so ist die Entropie 0

Huffman-Kodierung

Huffman-Code ist präfix-frei und eindeutig, optimal hinsichtlich Code-Effizienz

Kodierung erfolgt in zwei Schritten:

1. alle Symbole, geordnet nach abnehmenden Wahrscheinlichkeiten, untereinander schreiben; die letzten beiden zusammenfassen und in nächste Spalte einsortieren, so fortfahren, bis nur noch zwei Symbole vorhanden sind - den letzten beiden "0" und "1" zuordnen
2. Klammern derart beschriften, indem eine 0 oben und eine 1 unten steht. Huffman-Code ergibt sich wie folgt:
   1. vom Symbol aus waagrecht nach hinten gehen bis man auf Pfeile trifft, diesen folgen und der Klammer bis zum Ende folgen
   2. Anzahl der Klammern ergibt die Anzahl der Stellen des Codes
   3. den Code von hinten beginnend lesen

Kanalkodierung

Kanalkodierung (Überblick, Sinn, Formeln, Gütekriterien, Kodierungsarten)

Dient dazu, Fehler in der Übertragung der Symbole zu entdecken und eventuell auch zu korrigieren - gezieltes Hinzufügen von redundanter Information;

• Zwei Messgrößen für die Fehlerperformance:
  • BER (Bit Error Rate): mittlere Rate zu der Fehler auftreten $\rightarrow P_{b}\cdot R_{b}$ (wobei $R_{b}$ Bitübertragungsrate des Kanals ist)
  • $P_{b}$: bekannte Wahrscheinlichkeit eines Bitfehlers

• Gütekriterien
  • Hammingdistanz gibt an, um wieviele Bits sich zwei Codewörter unterscheiden, d.h. wie leicht es ist ein Codewort falsch als ein anderes zu interpretieren
  • Gewicht eines Codewortes gibt an, wieviele Einsen das Codewort enthält

ARQ und FECC

Automatic Repeat Request (ARQ)

Wird ein Fehler in der Übertragung erkannt, so fordert der Empfänger über einen Feedback-Kanal den fehlerhaften Datenblock erneut an; ist bei langsamen Links wie Satellitenübertragung oft keine Option, hier benötigt man FECC

Prinzipiell zwei Techniken, bei beiden wird Datenblock vom Sender erneut übertragen, sofern dieser nicht innerhalb eines gewissen Time-Outs eine Rückmeldung (weder positive noch negative) erhalten hat

• stop and wait ARQ: jeder Datenblock wird vom Empfänger als positiv oder negativ bestätigt, bevor ein neuer Datenblock übertragen wird
• continuous ARQ: Datenblöcke werden gesendet, ohne die empfängerseitige Bestätigung abzuwarten
  • go-back-N: jeder Datenblock hat Sequenznummer N; jedes Quittungssignal enthält die Sequenznummer eines Datenblocks und bestätigt damit den Empfang aller Datenblöcke bis N-1; bei Time-Out oder einer negativen Quittierung werden alle Datenblöcke ab dem fehlerhaften erneut übertragen
  • selective repeat: nur Datenblöcke mit negativer Quittierung bzw. Time-Out werden erneut übertragen; hier müssen die ankommenden Pakete eventuell umgeordnet werden, das ist bei go-back-N nicht nötig

Forward Error Correction Coding (FECC)

Mittels data check bits wird unter den Informationsbits Redundanz implementiert

Nachteil: benötigte Zeit um die Nachrichten zusammenzusetzen und empfängerseitig zu prüfen, Hardwarekomplexität ist heutzutage jedoch kein nennenswertes Problem mehr ($\rightarrow$ VLSI-Technologie)

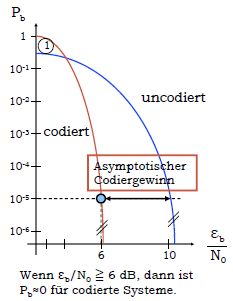
Schwelleneffekt bei der Bitfehlerwahrscheinlichkeit

Fundamentale Zusammenhänge:

• Leistungseffizienz: minimales Signalstörleistungsverhältnis für eine hinreichend zuverlässige digitale Übertragung

• ${\frac {\mathrm {E} _{b}}{N_{0}}}$ = Äquivalente mittlere Signalenergie je Bit übertragener Information / Einseitige spektrale Rauschleistungsdichte

$\Rightarrow$ Verursacht durch das schlechte SNR im Bereich (1) baut der Decoder, beim Versuch die Fehler zu korrigieren, mehr Fehler ein als ursprünglich vorhanden waren

n-k Blockcodes

Blockkodierer (relevant im Bereich der Kanalkodierung) nimmt ein k-stelliges Informationswort und macht daraus ein n-stelliges kodiertes Codewort

• n-stelliges Codewort besteht daher aus k Informationsbits und (n-k) redundanter Paritätsbits (d.h. n ist immer größer als k, n > k)

• Rate oder Effizienz des Codes: $R={\frac {k}{n}}$

Lineare Gruppencodes

Stellen die größte Gruppe der Blockcodes dar

Codewörter eines linearen Gruppencodes haben eine direkte Beziehung mit den Elementen einer mathematischen Gruppe

• d.h. durch Modulo-2-Addition zweier Codewörter ergibt sich immer ein anderes Codewort, d.h. die Gruppe ist abgeschlossen

Dekoderstrategien für lineare Blockcodes

1. Nearest Neighbour
2. Maximum-Likelihood

Faltungscodes

Ausgabedaten = Eingabedaten * Impulsantwort des Kodierers (* = Faltung)

Untergruppe von Gruppencodes, durch zyklische Eigenschaft kann das Nullwort nicht verarbeitet werden

Eigenschaften:

• mathematische Struktur erlaubt Codes zu erzeugen, welche eine bessere Korrektureigenschaft besitzen
• Die Codes können in einfache Hardwarestruktur umgesetzt werden: Schieberegister und EXOR
• alle Codewörter gehen durch zyklische Verschiebung hervor
• zyklische Codes werden durch Polynome erzeugt

Bitfehlerwahrscheinlichkeit vor und nach der Kanalkodierung

TODO

Die Bitfehlerwahrscheinlichkeit verändert sich nicht, jedoch kann man jetzt eine bestimmte Anzahl an Bitfehlern korrigieren (?)

Shannon'sches Kapazitätstheorem

(zu finden in Wikipedia unter "Shannon-Hartley-Gesetz")

Für einen AWGN-Kanal existiert immer ein Kodierverfahren, sodass eine fehlerfreie Übertragung möglich ist, solange die Datenrate $R_{b}$ kleiner als die Kanalkapazität $C$ bleibt:

$C=B\cdot ld(1+{\frac {S}{n}})=B\cdot ld(1+{\frac {S}{N_{0}\cdot B}})$

$C$ ... maximal mögliche Bitrate

$S$ ... pro Symbol aufgewendete Leistung

$N$ ... spektral konstante Rauschleistung

$N_{0}$ ... Rauschleistungsdichte

Theorem gibt jedoch keine Auskunft darüber, wie das Kodierverfahren gestaltet sein muss

Modulation mit einem sinusförmigen Trägersignal

Trägermodulation

Bewirkt eine Frequenzumsetzung, wobei die Information des Basisbandsignals dem Trägersignal eindeutig umkehrbar aufgeprägt wird

• Basisbandlage (BB): Spektrum von $-f_{B}$ ... $+f_{B}$ (Zentrum 0)
• Bandpasslage (BP): Spektrum von $-f_{B}+f_{0}$ ... $+f_{B}+f_{0}$ (Zentrum $f_{0}$)

• UP-Conversion: Verschiebung Spektrum von BB-Lage in BP-Lage ($\rightarrow$ Modulation)
• Down-Conversion: Verschiebung Spektrum von BP-Lage in BB-Lage ($\rightarrow$ Demodulation)

Vorteile / Ziele die man damit erreichen kann:

• Signale können an Charakteristika des Übertragungskanals besser angepasst werden
• Störungen in BP-Lage geringer
• Funkübertragung möglich
• Verwendung von FDMA möglich; für jeden Teilnehmer eigenes Frequenzband
• Verwendung von effizienten Antennen möglich (mit kleinen Abmessungen)
• Filter sind nur in bestimmten Frequenzbereichen ökonomisch herzustellen

Wie funktioniert die UP-Conversion?

• Verschieben eines Spektrums $D(f)$ mit Zentrum $f=0$ in eine neue Lage mit Zentrum $f=f_{0}$ erreicht man durch Faltung von $D(f)$ einem Dirak an der Stelle $f_{0}$

• Ein um den Ursprung symmetrisches Dirakpaar entspricht einer Kosinusfunktion
• Frequenzverschiebung wurde durch Faltung erreicht, Faltung entspricht im Zeitbereich einer Multiplikation, also
  • UP-Conversion durch Multiplikation des Basisbandsignals mit einer Kosinusfunktion: $g(t)=d(t)\cdot cos(2\pi f_{0}t)$

Einteilung der BP-Modulation

Basiert auf den Möglichkeiten die Information einem sinusförmigen Trägersignal in eindeutiger Weise aufzuprägen; auf welche Eigenschaft des Trägersignals wird Information abgebildet?

• auf Amplitude $\Rightarrow$ Amplitude Shift Keying (ASK)
• auf Frequenz $\Rightarrow$ Frequency Shift Keying (FSK)
• auf Phase $\Rightarrow$ Phase Shift Keying (PSK)

Wird die Information binär übertragen, so benötigt man zur Unterscheidung nur zwei Trägerzustände $\Rightarrow$ BASK, BFSK, BPSK (B... "binary")

Werden die Bits zu Symbolen zusammengefasst und existieren M solcher Symbole, so muss der Träger M eindeutige Unterscheidungsmerkmale besitzen $\Rightarrow$ MASK, MFSK, MPSK

Gütekriterien

Spektrale Effizienz

Ist ein Maß für den Informationstransfer pro eingesetztem Herz Bandbreite.

$\eta _{S}={\frac {R_{s}\cdot H}{B}}$ .... $[{\frac {\frac {Bit}{s}}{Hz}}]$

Leistungseffizienz

Ist ein Maß für die benötigte Signalleistung um eine vorgegebene SEP zu erreichen.

TODO

BASK, OOK, Erkennung von OOK-Signalen

Modulation durch Änderung der Amplitude

Wenn bei BASK eine der beiden Amplituden auf Nullpegel festgelegt wird, spricht man von On-Off Keying (OOK); Realisierung mittels einfachem Schalter, der das Trägersignal ein- und ausschaltet, oder als Multiplikator, der den Träger mit einem unipolaren Basisband-OOK-Signal multipliziert $\rightarrow$ das Spektrum des Basisbandsignals wird durch die IF Modulation rund um die Trägerfrequenz $f_{c}$ reproduziert

Erkennung von OOK-Signalen kann grundsätzlich auf zwei Arten erfolgen:

• koheränter Empfang:
  • Phasenlage des empfangenen Signals ist von Bedeutung
  • Einsatz von Matched Filter oder Korrelatoren vor dem Sampling, da diese ja von der Phase abhängen. Verglichen wird jeweils mit dem Trägersignal, also der Sinusschwingung

• inkoheränter Empfang:
  • Phasenlage des empfangenen Signals ist nicht von Bedeutung
  • Einsatz von Hüllkurvendetektor gefolgt von centre point Abtastung oder I+D Entscheidung.
  • Alternativ: Umsetzung mit zwei Korrelationskanälen, einer für Inphase und anderer für Quadraturkomponenten

Bandbreite eines BASK-Signals: $B=2\cdot f_{0}$

BPSK, PRK, Erkennung von PRK-Signalen

Modulation durch Änderung der Phase

Sind die Zeiger von null und eins bei BPSK antipodal (d.h. um 180° verschieden), so spricht man von Phase Reversal Keying (PRK)

Zur Erkennung sind natürlich nur koheränte Empfänger geeignet, wobei bei PRK nur ein Matched Filter/Korrelator nötig ist, denn bei 180° Phasenverschiebung liefert der Korrelator/Filter $k_{E}$ für 1 und $-k_{E}$ für 0

Bandbreite eines BPSK-Signals: $B=2\cdot f_{0}$

BFSK

Modulation durch Änderung der Frequenz

In der Praxis meist mittels numerisch gesteuerten Oszillator implementiert. Zum Empfang kann sowohl koheränter als auch inkoheränter Empfänger benutzt werden. Man braucht auf jeden Fall für jede der beiden Frequenzen einen eigenen Empfänger (z.B. zwei Korrelatoren)

Bandbreite eines BFSK-Signals: $B=f_{2}-f_{1}+2\cdot f_{0}$, wobei $f_{0}={\frac {1}{T_{0}}}$

Weitere Varianten von PSK, mit mehr als nur 2 Symbolen

Ziel dieser Varianten: Verbesserung der spektralen Effizienz

• M-symbol PSK (MPSK)
• Amplitude Phase Keying (APK): (M)ASK + MPSK
• Quadrature Phase Shift Keying (QPSK)
• Offset QPSK (OQPSK)
• Minumum Shift Keying (MSK): modifizierte Form von OQPSK

QPSK und OQPSK (bezeichnen, Unterschied)

Bei MPSK allgemein wird die PSK auf $M=2^{n}$ Symbole erweitert.

Speziell die 4-PSK kann als Superposition zweier PRK-Signale, die um $90^{\circ }$ phasenverschobene Träger (also $sin$ und $cos$ als Trägerfrequenz) benutzen, betrachtet werden.

$\Rightarrow$diese Variante wird dann als QPSK bezeichnet.

$\Rightarrow$man addiert also zwei PRK-Signale mit Amplitude ${\frac {A}{\sqrt {2}}}$ mit Bitrate ${\frac {R_{b}}{2}}$, die um $90^{\circ }$ phasensverschobene Träger benutzen (I und Q Kanal) und erhält QPSK mit Amplitude $A$ und Bitrate $R_{b}$

• Spektrale Effizienz von QPSK ist doppelt so hoch wie bei BPSK, da die Symbole in jedem Quadraturkanal den gleichen Spektralraum und die halbe Spektralbreite (halbe Übertragungsrate!) eines BPSK Signals gleicher Datenrate benötigen
• Fehlerwahrscheinlichkeit von QPSK ist höher als die von BPSK (die Phasen-Deltas sind kleiner), die Bitfehlerwahrscheinlichkeit ist jedoch gleich groß

Offset QPSK (OQPSK)

• identisch zu QPSK bis auf den Umstand, dass vor der Aufmodellierung auf den Träger der Datenstrom des Q-Kanals um eine QPSK-Bitdauer, also eine halbe QPSK-Symboldauer, versetzt wird.
• so findet nie auf beiden Kanälen gleichzeitig ein Null-Eins-Übergang statt $\Rightarrow$ Phasensprünge von $180^{\circ }$ werden unterbunden
• ein $180^{\circ }$ Sprung wird also in zwei $90^{\circ }$ Sprünge aufgeteilt die im Abstand von dieser QPSK-Bitdauer erfolgen
• Übergänge treten so häufiger auf, ihre Auswirkungen sind allerdings geringer (spektrale Effizienz von OQPSK und QPSK sind gleich)
• Vorteil von OQPSK: nichtlineare Effekte (wie sie Filter und Übertragungskanäle etc. haben) beeinflussen durch die kleineren Phasensprünge von $90^{\circ }$ statt der $180^{\circ }$ bei QPSK die Übertragungsqualität weniger

Unterschied zwischen QPSK und PRK

TODO

MSK

TODO

Rauschen und Link-Budget

TODO

Mobile Kommunikation

Probleme die der Mobilfunkkanal verursacht

Nachteile im Vergleich mit stationären Sichtverbindungen:

• Doppler-Verschiebungen in der Trägerfrequenz durch die Bewegung der Stationen relativ zueinander
• Langsame Schwankungen der Signalstärke im Raum, verursacht von Hindernissen (Funkschatten)
• Schnelle Schwankungen der Signalstärke im Raum durch Interferenz mehrerer, auf unterschiedlichen Pfaden gereisten Signalen
• Schwankungen der Signalstärke in der Zeit wegen der Bewegung durch ein sich räumlich änderndes Feld
• Frequenzabhängige Schwankungen der Übertragungsfunktion bei Breitbandsignalen
• Dispersion in der Zeit durch Mehrwegeausbreitung
• Änderung der Kanaleigenschaften (Übertragungsfunktion) über der Zeit durch die Bewegung

Schnelle und langsame Schwunderscheinungen

Langsame Schwunderscheinungen:

• erzeugt von Verschattungen durch Hindernisse, Beugungseffekte
• räumliche Skala: im Bereich von einigen 10 Metern (urbaner Bereich)
• Statistik: empfangene Trägerleistung gehorcht einer Log-Normal Statistik.

Schnelle Schwunderscheinungen:

• erzeugt durch Interferenz mehrerer Signalpfade (konstruktive und destruktive Interferenz der Mehrwegeausbreitung)
• räumliche Skala: im Bereich einer halben Wellenlänge
• Statistik: empfangene Trägerleistung gehorcht einer
  • Rayleigh-Statistik, wenn keine Sichtverbindung zwischen Sender und Empfänger besteht
  • Rice-Statistik, wenn Sichtverbindung besteht

Störungen und Gegenmaßnahmen

TODO

CDMA

TODO

TDMA

TODO