TU Wien:Einführung in wissensbasierte Systeme VU (Egly)/Prüfung 2012-07-02

Angabe

Beispiel 1 : Logikbasierte Wissensrepräsentation

• a) (12 Punkte) Gegeben sei folgende Wissensbasis $\phi :\forall x[P(x)\rightarrow (Q(x)\lor R(x))]\land (\exists x(R(x))\rightarrow P(c))$ und die Anfrageformen $\psi :\neg Q(a)\land P(b)\rightarrow P(c)$, wobei a, b und c Konstanten sind. Stellen Sie fest, ob aus der Wissensbasis $\phi$ auf $\psi$ geschlossen werden kann. Gehen Sie dabei in folgenden Schritten vor und legen Sie Wert auf eine exakte Darstellung. Geben sie den Zusammenhang zwischen den in der Transformation entstehenden Problemen an.
  1. Stellen Sie die Aussage als ein Entailmentproblem dar.
  2. Überprüfen Sie semantisch, ob die Entailmentbeziehung gilt. Gehen Sie dabei so vor, dass Sie zeigen, dass jedes Modell von $\phi$ auch ein Modell von $\psi$ ist oder konstruieren Sie ein Gegenbeispiel.

• b) (4,5 Punkte) Bestimmen Sie ob die folgenden Formeln gültig, widerlegbar, erfüllbar, Tautologien oder eine Kontradiktionen sind.
  1. $p\rightarrow (q\lor \neg p)$
  2. $((p\land q)\rightarrow \neg q)\rightarrow (p\leftrightarrow \neg p)$
  3. $(\neg p\rightarrow \neg q)\rightarrow p$

• c) (13,5 Punkte) Gegeben einen Wissensbasis $\phi$ und eine Anfrage $\psi$. Zeigen Sie, dass $\phi \models \psi$ genau dann gilt, wenn $\phi \rightarrow \psi$ gültig ist.

Beispiel 2 : Probabilistisches Schließen

• a) (6 Punkte) Was versteht man unter Marginalisierung im Bezug auf Wahrscheinlichkeitsverteilungen?
• b) (6 Punkte) Leiten Sie das Bayes'sche Gesetz aus der Produktregel her.
• c) (8 Punkte) Was ist ein Bayes'sches Netz (Grundidee, Komponenten)? Welche Unabhängigkeitsannahmen gelten in einem Bayes'schem Netz?

• d) Gegeben ist folgender Graph eines Bayes'schen Netzes:
  
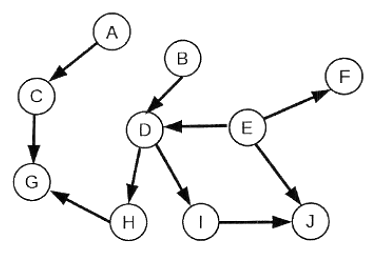
  Welche der folgenden Eigenschaften treffen zu:
  1. J ist bedingt unabhängig von F bei Evidenz H.
  2. G ist bedingt unabhängig von A bei Evidenz D und J.
  3. I ist nicht bedingt unabhängig von F bei Evidenz D.
  4. H ist bedingt unabhängig von A bei Evidenz B.

Beispiel 3 : Nichtmonotones Schließen

• a) (6 Punkte) Closed World Assumption: Geben Sie eine aussagenlogische Theorie T an, sodass folgende zwei Bedingungen gleichzeitig erfüllt sind:
  • i) die CWA von T ist inkonsistent
  • ii) die CWA von T ist zu p konsistent (wobei p ein Atom ist).
• b) (6 Punkte) Angenommen $T_{1}$ ist eine beliebige, konsistente Wissensbasis und $T_{2}$ ist eine inkonsistente Wissensbasis. Welche Beziehung besteht zwischen $Cn(T_{1})$ und $Cn(T_{2})$?
• c) (6 Punkte) Was versteht man unter Nichtmonotonie einer Inferenzrelation?
• d) (6 Punkte) Gegeben sein folgende Mengen (p, q, r und s sind aussagenlogische Konstanten):
  • $\Delta =\left\lbrace {\frac {r:\neg s}{q}},{\frac {:\neg r}{\neg r}},{\frac {\neg q:r}{p}},{\frac {p,r,q:s}{\neg s}}\right\rbrace$
  • ${\begin{aligned}W_{1}&=\{r,q\},&W_{2}&=\{\neg s\},&W_{3}&=\{p\}\\E_{1}&=Cn(W_{1}),&E_{2}&=Cn(W_{2}\cup \{\neg q,p\}),&E_{3}&=Cn(W_{3}\cup \{r\})\end{aligned}}$
    
    
  • i) Geben Sie die klassischen Redukte $\Delta _{E_{i}}$ von $\Delta$ bezüglich der Mengen $E_{i},\,i=1,2,3$ an.
  • ii) Markieren sie die korrekten Aussagen
    • 1) $E_{1}$ ist eine Extension der Default Theorie $T_{1}=(W_{1},\Delta )$
    • 2) $E_{2}$ ist eine Extension der Default Theorie $T_{2}=(W_{2},\Delta )$
    • 3) $E_{3}$ ist eine Extension der Default Theorie $T_{3}=(W_{3},\Delta )$

Beispiel 4 : Answer Set Programming (ASP)

• a) (8 Punkte) Sei M eine Interpretation und P ein grundiertes Programm.
  • i) Definieren Sie den Begriff des Reduktes $P^{M}$
  • ii) Wann ist I ein Answer Set von P?

• b) (6 Punkte) Gegeben sei folgende Programme (a und b sind Grundatome): $P=\{a:-\,{\text{not }}a,a:-\,a\}$ $Q=\{b:-\,{\text{not }}b,a:-\,a\}$. Für welche der folgende Programme ist $\{a\}$ ein Answer Set?
  • i) $P\cup \{a\}$
  • ii) $Q\cup \{a\}$
  • iii) $P\cup Q\cup \{a:-\,{\text{not }}b,b:-\,{\text{not }}a\}$

• c) (4 Punkte) Dürfen Programmregeln für konsistenz-basierte Diagnosen in DLV Disjunktionen enthalten?
• d) (5 Punkte) Was versteht man unter einer abduktiven Diagnose eines abduktiven Diagnose Problems ${\mathcal {P}}=\langle H,T,O\rangle$?
• e) (7 Punkte) Gegeben sei folgende Beschreibung eines Rechenelements C: falls C nicht defekt ist, am Eingang 1 von C der Wert V1 anliegt und am Eingang 2 von C der Wert V2 anliegt, dann liegt am Ausgang von C der Wert V1 * V2 an, vorausgesetzt V1 > 0, ansonsten liegt am Ausgang von C2 der Wert V2 an. Repräsentieren Sie dies durch logische Programmregeln.

Ausarbeitung

Logikbasierte Wissensrepräsentation

• a) (12 Punkte) Gegeben sei folgende Wissensbasis phi: Vx[P(X) -> (Q(x) v R(X))] ^ (Ex(R(X)) -> P(c)) und die Anfrageformen psi: -Q(a) ^ P(b) -> P(c), wobei a, b und c Konstanten sind. Stellen Sie fest, ob aus der Wissensbasis phi auf psi geschlossen werden kann. Gehen Sie dabei in folgenden Schritten vor und legen Sie Wert auf eine exakte Darstellung. Geben sie den Zusammenhang zwischen den in der Transformation entstehenden Problemen an.
  • 1) Stellen Sie die Aussage als ein Entailmentproblem dar.
  • 2) Überprüfen Sie semantisch, ob die Entailmentbeziehung gilt. Gehen sie dabei so vor, dass Sie zeigen, dass jedes Modell von phi auch ein Modell von psi ist oder konstruieren Sie einen Gegenbeispiel.

Meine Lösung (hamberga):

1) $\phi$ |= $\psi$

2) Semantisch prüfen:

i) ich gehe davon aus, dass die Beziehung nicht hält und beginne ein Modell zu finden, das für phi ein Modell ist und für psi nicht.

I($\phi$) = True

I($\psi$) = False

ii) aus I($\psi$) = False kann man schließen dass I(P(c))=False, I(Q(a))=False, I(P(b))=True, weil ansonsten die Implikation nicht False werden kann.

iii) Den Rest der Interpretationswerte fülle ich so auf, dass phi gültig ist.

Das ergibt bei mir folgendes Modell $\alpha$:

I(P(a)) = False, I(R(a)) = True, I(Q(a)) = False

I(P(b)) = True, I(R(b)) = False, I(Q(b)) = True

I(P(c)) = False, I(R(c)) = False, I(Q(c)) = False

I($\phi$)= True

I($\psi$)= False

//EDIT: ich hab da 2 Punkte abgezogen bekommen, weil ich die Domain nicht angegeben habe. Wäre das in dem Fall dann einfach U = {a,b,c}?

Meine Überlegung wie man auf ein (anderes) Gegenbeispiel kommt

Es fehlen noch Werte für (immer I(..)) P(a), Q(b), Q(c), R(a), R(b), R(c).

Es muss gelten: (Ex(R(X)) -> P(c)), aber für welches x? (a, b oder c)

da I(P(c)) = false muss für das x gelten I(R(x)) = false.

Kandidat a: I(R(a)) = false, daraus folgt P(a) -> (false v false), also I(P(a)) = false

Fehlen noch Q(b), Q(c), R(b), R(c).

Weiters muss gelten: P(b) -> (Q(b) v R(b)) = true -> (Q(b) v R(b)), ich wähle: I(Q(b)) = true, I(R(b)) = true.

Fehlen noch Q(c), R(c).

Hier gilt: false -> (Q(c) v R(c)), also I(Q(c)) = false, I(R(c)) = false.

Das Gegenbeispiel kann also lauten:

I(P(a)) = false, I(R(a)) = false, I(Q(a)) = false

I(P(b)) = true, [I(R(b)) = false, I(Q(b)) = true] ODER [I(R(b)) = true, I(Q(b)) = false)] ODER [I(R(b)) = true, I(Q(b)) = true]

I(P(c)) = false, I(R(c)) = false/true, I(Q(c)) = false/true

Ich hoffe ich hab mich nich geirrt. Einwände? Nudelarmiger (Diskussion) 15:01, 2. Nov. 2012 (CET)

Die oben genannten Möglichkeiten sollten alle als Gegenbeispiel hinhauen. Sollte aber vielleicht noch jemand überprüfen. Nudelarmiger (Diskussion) 12:53, 9. Nov. 2012 (CET)

• b) (4,5 Punkte)
  • 1) p -> (q v -p) [widerlegbar, erfüllbar]
  • 2) ((p ^ q) -> -q) -> (p <-> -p) [widerlegbar, erfüllbar]
  • 3) (-p -> -q) -> p [widerlegbar, erfüllbar]

Was war hier gefragt? Ankreuzeln was zutrifft? Nudelarmiger (Diskussion) 15:06, 2. Nov. 2012 (CET)

• c) (13,5 Punkte) Gegeben einen Wissensbasis phi und eine Anfrage psi. Zeigen Sie, dass phi |= psi genau dann gilt wenn phi -> psi gültig ist.

Meine Lösung (hamberga):

phi |= psi // 1.) Deduktionstheorem anwenden

|= phi -> psi // 2.) ist schon die Lösung

(Vermutlich müsste man den Beweis aber genauer führen, ohne das Deduktionstheorem als gegeben zu nehmen. Dieser wäre im Skriptum "Theoretische Informatik und Logik" bei Satz 3.31 auf Seite 111 zu finden) Frage dazu (testsieger): Aber ist das, was es hier zu beweisen gibt, nicht genau das Deduktionstheorem

IMHO muss man hier den Beweis für das Deduktionstheorem hinschreiben. Siehe auch Datei:TU Wien-Einführung in wissensbasierte Systeme VU (Egly) - Beweis Deduktionstheorem.pdf

Probabilistisches Schließen

• a) (6 Punkte) Was versteht man unter Marginalisierung im Bezug auf Wahrscheinlichkeitsverteilungen? [prob.pdf 11]

• b) (6 Punkte) Leiten Sie das Bayer'sche Gesetz aus der Produktregel her.

Hab ich so in prob.pdf Seite 15 gefunden. Ich hoffe das passt so.

Produktregel:

P(A,B)=P(A|B)*P(B)

P(A,B)=P(B|A)*P(A)

Gleichsetzten:

P(A|B)*P(B)=P(B|A)*P(A)

P(B) auf die andere Seite bringen:

P(A|B)=(P(B|A)*P(A))/P(B)

• c) (8 Punkte) Was ist ein Bayes'sches Netz (Grundidee, Komponenten)? Welche Unabhängigkeitsannahmen gelten in einem Bayes'schem Netz? [prob.pdf 23f]

• d) Gegeben ist folgender Graph eines Bayes'schen Netzes:

Welche der folgenden Eigenschaften treffen zu:

• J ist bedingt unabhängig von F bei Evidenz H. falsch
• G ist bedingt unabhängig von A bei Evidenz D und J. falsch
• I ist nicht bedingt unabhängig von F bei Evidenz D. falsch
• H ist bedingt unabhängig von A bei Evidenz B. richtig

Nichtmonotones Schließen

• a) (6 Punkte) Closed World Assumption: Geben Sie eine aussagenlogische Theorie T an, sodass folgende zwei Bedingungen gleichzeitig erfüllt sind:
  • i) die CWA von T ist inkonsistent
  • ii) die CWA von T ist zu p konsistent (wobei p ein Atom ist).

T = { p v q }

• b) (6 Punkte) Angenommen T1 ist eine beliebige, konsistente Wissensbasis und T2 ist eine inkonsistente Wissensbasis. Welche Beziehung besteht zwischen Cn(T1) und Cn(T2)?

$Cn(T_{1})\subset Cn(T_{2})$ , da eine konsistente Theorie niemals die Menge aller Formeln sein kann.

• c) (6 Punkte) Was versteht man unter Nichtmonotonie einer Inferenzrelation?

Eine Inferenzrelation $\vdash$ erfüllt die Nichtmonotonie dann und nur dann, wenn es eine Theorie $\Gamma$ und Formeln $\varphi ,\psi$ gibt, sodass $\Gamma \vdash \varphi$, jedoch nicht $\Gamma ,\psi \vdash \varphi$ gilt.

• d) (6 Punkte) Gegeben sein folgende Mengen (p, q, r und s sind aussagenlogische Konstanten):

delta={ r:-s/q, :-r/-r, -q:r/p, p,r,q:s/-s} W1={r,q}, E1=Cn(W1), W2={-s}, E2=Cn(W2 & {-q,p}), W3={p}, E3=Cn(W3 & {r})

• • Geben Sie die klassischen Redukte delta Ei von delta bezüglich der Mengen Ei an, für i=1,2,3

delta E1={r/q, -q/p, p,r,q/-s} delta E2={r/q, /-r, -q/p} delta E3={r/q, -q/p, p,r,q/-s}

• • Markieren sie die korrekten Aussagen
    • 1) E1 ist eine Extension der Default Theorie T1=(W1,delta) [richtig]
    • 2) E2 ist eine Extension der Default Theorie T2=(W2,delta) [falsch]
    • 3) E3 ist eine Extension der Default Theorie T3=(W3,delta) [falsch]

Answer Set Programming (ASP)

• a) (8 Punkte) Sei M eine Interpretation und P ein grundiertes Programm.
  • 1. Definieren Sie den Begriff des Reduktes P^M [asp2.pdf 5]
  • 2. Wann ist I ein Answer Set von P? [asp2.pdf 5]

• b) (6 Punkte) Gegeben sei folgende Programme (a und b sind Grundatome):

P={a :- not a, a :- a}, Q={b :- not b, a :- a}. Für welche der folgende Programme ist {a} ein Answer Set?

• • i) P & {a} [yes]
  • ii) Q & {a} [no]
  • iii) P & Q & {a :- not b, b :- not a} [no]

• c) (4 Punkte) Dürfen Programmregeln für konsistenz-basierte Diagnosen in DLV Disjunktionen enthalten? [no]

• d) (5 Punkte) Was versteht man unter einer abduktiven Diagnose eines abduktiven Diagnose Problems <H,T,O>? [asp2.pdf 31]

• e) (7 Punkte) Gegeben sei folgende Beschreibung eines Rechenelements C: falls C nicht defekt ist, am Eingang 1 von C der Wert V1 anliegt und am Eingang 2 von C der Wert V2 anliegt, dann liegt am Ausgang von C der Wert V1 * V2 an, vorausgesetzt V1 > 0, ansonsten liegt am Ausgang von C2 der Wert V2 an. Repräsentieren Sie dies durch logische Programmregeln.
  • out(C, V) :- calculator(C), not ab(C), in1(C, V1), in2(C, V2), V1 > 0, V = V1 * V2.
  • out(C, V) :- calculator(C), not ab(C), in1(C, V1), in2(C, V2), V1 <= 0, V = V2.

Anmerkung: ich hab das mal korrigiert, und zwar gehen laut Angabe die Bedingungen nicht auf V2 sondern auf V1, und ich habs mit <= 0 und > 0 gelöst, damit sicher alle Fälle abgedeckt sind. Bin mir nicht sicher, ob < 1 wirklich dasselbe ist wie <= 0, so in der Form wie es jetzt ist hab ich auf jeden Fall alle Punkte bekommen.