TU Wien:Einführung in wissensbasierte Systeme VU (Egly)/Prüfung 2014-01-29/Beispiel 4

Probabilistisches Schließen:

Teilaufgabe a)

Erklären Sie die Begriffe Diagnostisches Schließen, Kausales Schließen und Interkausales Schließen im Zusammenhang mit Bayes'schen Netzen und geben Sie jeweils ein kleines Beispiel zur Illustration jedes Begriffes an. (3 Punkte)

Lösungsvorschlag von --JasonLeroy (Diskussion) 23:49, 24. Apr. 2014 (CEST)

(siehe prob2.pdf, Seite 15)

Diagnostisches Schließen: Von der Auswirkung zur Begründung. Beispiel: $P(\neg L|\neg M)$ => Wahrscheinlichkeit, dass der Block zu schwer war unter der Voraussetzung, dass der Block nicht bewegt wurde.

Kausales Schließen: Von einer Begründung zur Auswirkung. Beispiel: $P(M|L)$ => Wahrscheinlichkeit, dass ein Block vom Roboter bewegt wurde unter der Voraussetzung, dass der Block nicht zu schwer ist.

Interkausales Schließen: Kombination aus diagnostisch und kausal. Beispiel: $P(\neg L|\neg B,\neg M)$ => Die Wahrscheinlichkeit für $L$ sinkt, nachdem $B$ eine Voraussetzung für $M$ ist, und beide nicht eintreten. (?)

Lösungsvorschlag von --Tailorian (Diskussion) 13:23, 11. Jun. 2015 (CEST)

(siehe prob.pdf, Seite 29) Inferenztypen

Diagnostisches Schließen: Von Effekten zu Ursachen:

Beispiel: $P(\neg L|\neg M)$ => liefert die Wahrscheinlichkeit, dass der Block zu schwer war unter der Voraussetzung, dass der Block nicht vom Roboter bewegt wurde

Kausales Schließen: Von Ursachen zu Effekten

Beispiel: $P(M|L)$ => liefert die Wahrscheinlichkeit, dass der Roboter den Block bewegt hat unter der Voraussetzung, dass der Block nicht zu schwer ist

Interkausales Schließen Zwischen Ursachen eines gemeinsamen Effekts

Beispiel: $P(\neg L|\neg B,\neg M)$ => unter der zusätzlichen Evidenz $\neg B$ gegeben $\neg M$, das Event $\neg L$ wird unwahrscheinlicher denn $\neg B$ ist eine Ursache von $\neg M$

Teilaufgabe b)

Kreuzen Sie bei den folgenden Aussagen an, ob sie richtig sind oder nicht.

1. Zwei verschiedene Elementarereignisse können zugleich eintreten. richtig ☐ falsch ☐
2. Ein Bayes'sches Netz kann aus einem einzigen Knoten bestehen, der mit sich selbst verbunden ist. richtig ☐ falsch ☐
3. Es ist möglich, ein Bayes'sches Netz mit drei Knoten A, B und C zu konstruieren, dessen Topologie sicherstellt, dass notwendigerweise $P(A|C)\not =P(A)$ gilt. richtig ☐ falsch ☐

(3 Punkte)

Lösungsvorschlag von --JasonLeroy (Diskussion) 23:37, 24. Apr. 2014 (CEST)

1. richtig ☐ falsch ☒
2. richtig ☐ falsch ☒
3. richtig ☒ falsch ☐

Teilaufgabe c)

Was versteht man unter Marginalisierung im Bezug auf Wahrscheinlichkeitsverteilungen? (2.5 Punkte)

Teilaufgabe d)

Gegeben ist folgender Graph eines Bayes'schen Netzes:

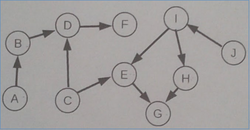
Welche der folgenden Eigenschaften treffen zu:

1. $E$ ist nicht bedingt unabhängig von $H$ bei Evidenz $B$. richtig ☐ falsch ☐
2. $F$ ist bedingt unabhängig von $A$ bei Evidenz $B$ und $G$. richtig ☐ falsch ☐
3. $D$ ist bedingt unabhängig von $A$ bei Evidenz $J$. richtig ☐ falsch ☐
4. $G$ ist bedingt unabhängig von $I$ bei Evidenz $D$. richtig ☐ falsch ☐

(4 Punkte)

Lösungsvorschlag von --JasonLeroy (Diskussion) 22:14, 26. Apr. 2014 (CEST)

1. richtig ☒ falsch ☐
2. richtig ☒ falsch ☐
3. richtig ☐ falsch ☒
4. richtig ☐ falsch ☒