TU Wien:Einführung in wissensbasierte Systeme VU (Egly)/Prüfung 2014-05-05/Beispiel 4

Probabilistisches Schließen

Teilaufgabe a)

Leiten Sie das Bayes'sche Gesetz aus der Produktregel her.

(3 Punkte)

Lösungsvorschlag von --JasonLeroy (Diskussion) 12:49, 27. Jan. 2015 (CET)

Die Produktregel: $P(V_{1},...,V_{n})=\prod _{i=1}^{n}P(V_{i}|V_{i+1},...,V_{n})$

Zwei Instanzen der Produktregel:

• $P(V_{i},V_{j})=P(V_{i}|V_{j})P(V_{j})$
• $P(V_{i},V_{j})=P(V_{j}|V_{i})P(V_{i})$

Gleichsetzen...

$P(V_{i}|V_{j})P(V_{j})=P(V_{j}|V_{i})P(V_{i})$

... und durch $P(V_{j})$ dividieren ...

$P(V_{i}|V_{j})={\frac {P(V_{j}|V_{i})P(V_{i})}{P(V_{j})}}$

Teilaufgabe b)

Entscheiden Sie, welche der folgenden Relation für beliebige Boole'sche Zufallsvariablen A und B gelten:

1. $P(a,b)+P(a,\neg b)=P(b)$ ☐ wahr ☐ falsch
2. $P(a|b)+P(a|\neg b)=1$ ☐ wahr ☐ falsch

(2 Punkte)

Lösungsvorschlag von --JasonLeroy (Diskussion) 10:03, 27. Jan. 2015 (CET)

(Laut Prüfungskorrektur)

1. ☐ wahr ☒ falsch
2. ☐ wahr ☒ falsch

Teilaufgabe c)

Was versteht man unter einer gemeinsamen Warhscheinlichkeitsverteilung (Joint Probability Distribution) über Zufallsvariablen $V_{1},...,V_{n}$?

(1.5 Punkte)

Lösungsvorschlag von --JasonLeroy (Diskussion) 12:57, 27. Jan. 2015 (CET)

$V_{1},...,V_{n}$ sind einige Zufallsvariablen und $\Omega$ ist die Menge aller atomaren Ereignisse über diese Zufallsvariablen.

Eine JPD von $V_{1},...,V_{n}$ ist eine Zuweisung $P$, die jedem atomaren Ereignis $\omega =(V_{1}=v_{1},...,V_{n}=v_{n})$ einen Wert $P(\omega )$ zuweist, sodass

1. $0\leq P(\omega )\leq 1$
2. $\sum _{\omega \in \Omega }P(\omega )=1$

Teilaufgabe d)

Welche der folgenden Eigenschaften treffen zu?

1. Angenommen Variablen $X_{1},X_{2},...,X_{k}$ haben keine Vorgänger in einem gegebenen Bayes-Netz, das insgesamt $n>k$ Variablen enthält. Dann legt das Bayes-Netz fest, dass $P(X_{1},X_{2},...,X_{k})=P(X_{1})P(X_{2})...P(X_{k})$. ☐ wahr ☐ falsch
2. Jede Boole'sche Funktion kann durch ein Bayes-Netz dargestetll werden. ☐ wahr ☐ falsch

(2 Punkte)

Lösungsvorschlag von --JasonLeroy (Diskussion) 10:07, 27. Jan. 2015 (CET)

(Laut Prüfungskorrektur)

1. ☒ wahr ☐ falsch Begründung: In einem Bayes-Netz gilt: $P(V_{1},...,V_{n})=\prod _{i=1}^{n}P(V_{i}|Parents(V_{i}))$, nachdem $X_{1},X_{2},...,X_{k}$ aber keine Vorgänger besitzen, so bleibt nur mehr $P(X_{1},...,X_{n})=\prod _{i=1}^{n}P(X_{i})$
2. ☒ wahr ☐ falsch

Teilaufgabe e)

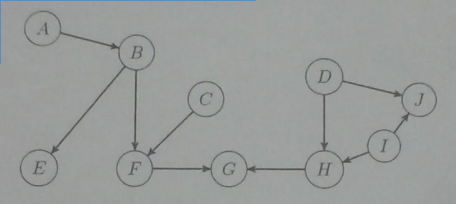
Gegeben ist folgender Graph eines Bayes'schen Netzes:

Welche der folgenden Eigenschaften treffen zu?

1. G ist bedingt unabhängig von A bei Evidenz B. ☐ wahr ☐ falsch
2. I ist bedingt unabhängig von A bei Evidenz C und J. ☐ wahr ☐ falsch
3. J ist bedingt unabhängig von H bei Evidenz D. ☐ wahr ☐ falsch
4. E ist nicht bedingt unabhängig von H bei Evidenz G. ☐ wahr ☐ falsch

(4 Punkte)

Lösungsvorschlag von --JasonLeroy (Diskussion) 10:10, 27. Jan. 2015 (CET)

(Laut Prüfungskorrektur)

1. ☒ wahr ☐ falsch
2. ☒ wahr ☐ falsch
3. ☐ wahr ☒ falsch
4. ☒ wahr ☐ falsch

Anmerkung von --Tyleet
Falschaussage2) ist nicht bedingt unabhängig. I->J<-D->H.... J hat 2 eingehende Kanten und ist in der Evidenzmenge -> D-Separation nicht gegeben.

Anmerkung von JasonLeroy zur Anmerkung Diese Begründung ist nicht ganz korrekt. J hat zwei eingehende Kanten, laut D-Separation blockiert es nur dann, wenn es nicht in der Evidenzmenge ist und auch dessen Nachfolger nicht in der Evidenzmenge sind.

Anmerkung von Exkalation (Diskussion) 14:54, 27. Jan. 2015 (CET): Bei 2 blockiert bereits G allein: Nicht in Evidenz, kein Child in Evidenz, zwei eingehende Kanten.

[vik_xxxl:Lösungsvorschlag]
all paths blocked => conditionaly independent

1. G _||_ A | B ?
A-B-F-G                   B blocks 1st sep
all paths blocked => conditionally independent => TRUE

2. I _||_ A | C,J ?
I- H-G-F-B-A              G blocks 3rd sep
I-J-D-H-G-F-B-A         G blocks 3rd sep
all paths blocked => conditionally independent => TRUE

3. J _||_ H | D ?
J-I-H                        no block
J-D-H                        D blocks 2nd sep.
NOT all paths blocked => NOT conditionally independent => FALSE

4. E _||_ H | G ?
E-B-F-G-H                   no block
NOT all paths blocked => NOT conditionally independent => TRUE

Anmerkung zu Lösungsvorschlag von vik_xxx: Argumentation stimmt bei allen. Danke!

Anmerkung bei 3 Es sollte NOT all paths blocked => NOT conditionally independent => TRUE sein. Danke für solche Knockout Single Choice Aufgaben LVA -Leitung >.>

Materialien

Neues Material hinzufügen

2

• 20140505 4 bayesnetz.png (details)