TU Wien:Einführung in wissensbasierte Systeme VU (Egly)/Prüfung 2018-03-15

Angabe

• Datei:TU Wien-Einführung in wissensbasierte Systeme VU (Egly) - Prüfung 2018-03-15.pdf

Beispiele

Beispiel 1: Logikbasierte Wissensrepräsentation

Beispiel 1a

Formulieren Sie folgendes Argument in der Prädikatenlogik und zeigen oder widerlegen Sie dessen Gültigkeit mittels TC1. Sollte das Argument nicht gültig sein, dann extrahieren Sie ein Gegenbeispiel aus dem Tableau.

Nicht alles was glänzt ist Gold. Schmuck glänzt. Somit ist Schmuck nicht aus Gold. (5 Punkte)

Beispiel 1b

Man zeige, dass $W\cup \{\phi \}\models \psi$ dann und nur dann gilt wenn $W\models \phi \to \psi$ auch gilt (Deduktionstheorem). Wenn Sie zusätzliche Theoreme aus der Vorlesung verwenden, so müssen Sie diese beweisen. (4 Punkte)

Beispiel 1c

Überprüfen Sie, welche Eigenschaften auf die nachfolgend angeführten aussagenlogischen Formeln zutreffen und kreuzen Sie jeweils alle zutreffenden Eigenschaften an. (4 Punkte)

Multiple Choice-Quiz:

Pluspunkt für eine richtige Antwort:
Punkt für eine falsche Antwort:
Ignoriere die Fragen-Koeffizienten:

1

$(p\vee (p\wedge q))\wedge \mathrm{\neg }p$

	gültig
	widerlegbar
	erfüllbar
	Tautologie
	Kontradiktion

2

$(p\vee q)\wedge (p\to q)$

	gültig
	widerlegbar
	erfüllbar
	Tautologie
	Kontradiktion

3

$(p\to q)\vee \mathrm{\neg }(\mathrm{\neg }q\wedge p)$

	gültig
	widerlegbar
	erfüllbar
	Tautologie
	Kontradiktion

4

$((a\to b)\wedge (b\to c))\to (a\to c)$

	gültig
	widerlegbar
	erfüllbar
	Tautologie
	Kontradiktion

Beispiel 1d

Kreuzen Sie Zutreffendes an: (4 Punkte)

Multiple Choice-Quiz:

Pluspunkt für eine richtige Antwort:
Punkt für eine falsche Antwort:
Ignoriere die Fragen-Koeffizienten:

1

TC1 kann für jede Formel ein Modell erzeugen. (unbewertet)

	richtig
	falsch

2

Die leere Disjunktion ist in allen Interpretationen wahr. (unbewertet)

	richtig
	falsch

3

$F\cup \{\phi \}\models \mathrm{\neg }\psi$ genau dann, wenn $F\cup \{\psi \}\models \mathrm{\neg }\phi$.

	richtig
	falsch

4

Alle Regeln des TC1 sind deterministisch. (unbewertet)

	richtig
	falsch

5

$\phi \leftrightarrow \psi$ ist gültig genau dann, wenn $\phi \leftrightarrow \mathrm{\neg }\psi$ unerfüllbar ist.

	richtig
	falsch

6

Ist $\phi$ unerfüllbar so ist $\mathrm{\forall }x(\phi \to \psi )$ gültig für beliebiges $\psi$.

	richtig
	falsch

7

Falls $\varphi$ erfüllbar ist, so ist $\mathrm{\neg }\varphi$ unerfüllbar.

	richtig
	falsch

8

TC1 terminiert immer.

	richtig
	falsch

Beispiel 2: Nichtmonotones Schließen

Beispiel 2a

Gegeben seien folgende Mengen (a ist ein Konstantensymbol, Q, R und P sind Prädikatensymbole):

$\Delta =\{\frac{P(a):Q(a),R(a)}{Q(a)},\frac{R(a):\mathrm{\neg }Q(a)}{\mathrm{\neg }Q(a)},\frac{Q(a):\mathrm{\neg }P(a)}{\mathrm{\neg }P(a)}\}$

$W_1=\{R(a),P(a)\},W_2=\{R(a),Q(a)\},W_3=\{R(a),P(a)\}.$

$E_1=Cn(W_1),E_2=Cn(W_2\cup \{\mathrm{\neg }P(A)\}),E_3=Cn(W_3\cup \{\mathrm{\neg }Q(a)\}).$

(i) Geben Sie die klassischen Redukte ${\Delta }^{E_i}$ von $\Delta$ bezüglich den Mengen $E_i$ an, für $i=1,2,3$. (3 Punkte)

(ii) Markieren Sie die korrekten Aussagen: (3 Punkte)

Multiple Choice-Quiz:

Pluspunkt für eine richtige Antwort:
Punkt für eine falsche Antwort:
Ignoriere die Fragen-Koeffizienten:

1

$E_1$ ist eine Extension der Default Theorie $T_1=⟨W_1,\Delta ⟩$.

	richtig
	falsch

2

$E_2$ ist eine Extension der Default Theorie $T_2=⟨W_2,\Delta ⟩$.

	richtig
	falsch

3

$E_3$ ist eine Extension der Default Theorie $T_3=⟨W_3,\Delta ⟩$.

	richtig
	falsch

Beispiel 2b

Gegeben ist folgende Wissensbasis T über eine Sprache mit den Konstantensymbolen a, b und c, dem Variablensymbol x und den einzigen Prädikatensymbolen P und Q:

$T=\{P(a),P(c)\vee Q(c),Q(b),\mathrm{\forall }x(Q(x)\to P(x))\}.$

(a) Geben Sie die Closed World Assumption CWA(T) von T an, indem Sie die folgende Gleichung ergänzen: $CWA(T)=Cn(T\cup \{\mathrm{...}\})$.

(b) Welche der folgenden Eigenschaften treffen zu?

(4 Punkte)

Multiple Choice-Quiz:

Pluspunkt für eine richtige Antwort:
Punkt für eine falsche Antwort:
Ignoriere die Fragen-Koeffizienten:

1

T ist deduktiv abgeschlossen.

	richtig
	falsch

2

CWA(T) ist konsistent.

	richtig
	falsch

Beispiel 2c

Definieren Sie den Abschluss einer offenen Default-Theorie $T=(W,\Delta )$. (4 Punkte)

Beispiel 2d

Was versteht man unter dem Monotonieprinzip der klassischen Logik? Geben Sie eine formale Definition an. (2 Punkte)

Beispiel 3: Answer-Set Programming

Beispiel 3a

Erklären Sie das Guess-and-Check Paradigma der Answer-Set Programmierung anhand eines Programmes, welche alle Vertex Cover eines Graphen berechnet.

Beachte: Sei $G=⟨V,E⟩$ ein Graph, wobei V die Menge der Knoten und E die Menge der Kanten des Graphen sei. Ein Vertex Cover ist eine Teilmenge S der Knotenmenge V sodass jede Kante von G mindestens einen Knoten in S besitzt. (6 Punkte)

Lösungsvorschläge

Lösungsvorschlag von Constantin

--Constantin 12:40, 3. Feb. 2021 (CET)

C(X) v ~C(X) :- V(X).

VC(X,Y) :- E(X,Y), C(X).
VC(X,Y) :- E(X,Y), C(Y).

:- E(X,Y), not VC(X,Y).

Testbeispiel

V(1).
V(2).
V(3).

E(1,3).
E(1,2).
E(2,3).

Beispiel 3b

Betrachten Sie die vier unten angegebenen Regeln, wo a und b propositionale Konstanten und X und Y Variablen sind. Kreuzen Sie an, ob die Aussagen richtig oder falsch sind. (2 Punkte)

Multiple Choice-Quiz:

Pluspunkt für eine richtige Antwort:
Punkt für eine falsche Antwort:
Ignoriere die Fragen-Koeffizienten:

1

$\leftarrow$ not P(X) ist ein Fakt.

	richtig
	falsch

2

$P(X)\vee \mathrm{\neg }P(Y)\leftarrow Q(X),R(Y)$ ist Horn. (unbewertet)

	richtig
	falsch

3

$a\leftarrow \mathrm{\neg }b$ ist basic.

	richtig
	falsch

4

$P(X)\leftarrow b,nota$ ist grundiert und normal.

	richtig
	falsch

Beispiel 3c

Was versteht man unter einer Abduktion und einem abduktiven Diagnoseproblem. (4 Punkte)

Beispiel 3d

Kreuzen Sie Zutreffendes an: (4 Punkte)

Multiple Choice-Quiz:

Pluspunkt für eine richtige Antwort:
Punkt für eine falsche Antwort:
Ignoriere die Fragen-Koeffizienten:

1

Bei Brave Reasoning ist eine Query nur dann wahr wenn sie auch in jedem Answer Set wahr ist. (unbewertet)

	richtig
	falsch

2

Regeln in einem Program zur konsistenzbasierten Diagnose müssen normal sein.

	richtig
	falsch

3

Jedes klassische Modell eines Programms ist auch ein Answer Set.

	richtig
	falsch

4

Disjunktion in ASP unterscheidet sich semantisch von Disjunktion in klassischer Logik.

	richtig
	falsch

Beispiel 4: Probabilistisches Schließen

Beispiel 4a

Angenommen, ein Test reagiert mit Sicherheit positiv, sollte eine bestimmte Krankheit vorliegen, zeigt aber auch zu 7% ein falsch-positives Resultat. Wenn man davon ausgeht, dass 1% der Bevölkerung von dieser Krankheit betroffen ist, und bei einer zufällig ausgewählten Person der Test positiv reagiert, wie groß ist die Wahrscheinlichkeit, dass die Person erkrankt ist?

Hinweis: Der konkrete numerische Wert muss nicht explizit berechnet werden; es genügt die Angabe der Formel mit den entsprechenden Werten. (5 Punkte)

Beispiel 4b

Bestimmen Sie die Richtigkeit oder Falschheit folgender Aussagen, für beliebige Boole'sche Zufallsvariablen A und B: (2 Punkte)

Multiple Choice-Quiz:

Pluspunkt für eine richtige Antwort:
Punkt für eine falsche Antwort:
Ignoriere die Fragen-Koeffizienten:

1

$P(A|\mathrm{\neg }B)+P(\mathrm{\neg }A|\mathrm{\neg }B)=1.$ (unbewertet)

	richtig
	falsch

2

$P(A,B)=P(A|B)P(B).$

	richtig
	falsch

Beispiel 4c

Was ist ein Bayes'sches Netz (Grundidee, Komponenten, Unabhängigkeitsannahmen, Berechnung der Wahrscheinlichkeiten)? (5 Punkte)

Beispiel 4d

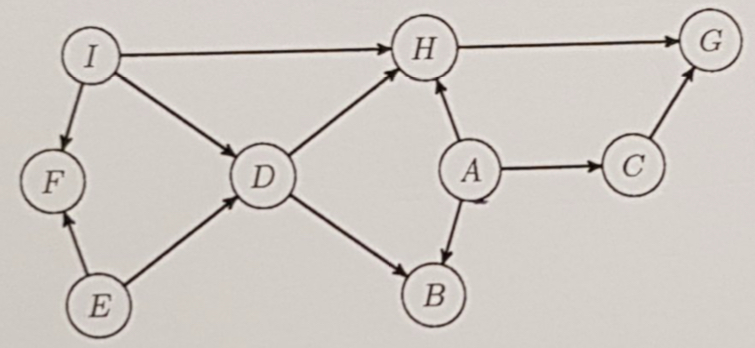
Gegeben ist folgender Graph eines Bayes'schen Netzes:

Welche der folgenden Eigenschaften treffen zu? (4 Punkte)

Multiple Choice-Quiz:

Pluspunkt für eine richtige Antwort:
Punkt für eine falsche Antwort:
Ignoriere die Fragen-Koeffizienten:

1

A ist bedingt unabhängig von D bei Evidenz B und H.

	richtig
	falsch

2

D ist bedingt unabhängig von G bei Evidenz C und H.

	richtig
	falsch

3

F ist bedingt unabhängig von C bei Evidenz D und H.

	richtig
	falsch

4

E ist bedingt unabhängig von B bei Evidenz D und F.

	richtig
	falsch

Materialien

Neues Material hinzufügen

E

• EWBS-Pruefung-2018-03-15-4d.jpeg (details)