TU Wien:Einführung in wissensbasierte Systeme VU (Egly)/Prüfung 2019-01-08

Angabe

• Datei:TU Wien-Einführung in wissensbasierte Systeme VU (Egly) - Prüfung 2019-01-08.pdf

Beispiele

Beispiel 1: Logikbasierte Wissensrepräsentation

Beispiel 1a

Definieren Sie den Begriff einer Interpretationsstruktur in der Prädikatenlogik erster Stufe. Erklären Sie den Unterschied zwischen einer Interpretationsstruktur und einem Modell. Zeigen oder widerlegen Sie mithilfe einer Interpretationsstruktur, dass für beliebige geschlossene Formeln $\varphi ,\psi$ und $\rho$ aus $\psi \vDash \varphi \land \rho$ immer $\psi \vDash \rho$ folgt. Wenn Sie zusätzliche Theoreme aus der Vorlesung verwenden, so müssen Sie diese beweisen. (5 Punkte)

Beispiel 1b

Formulieren Sie folgendes Argument in Prädikatenlogik und zeigen oder widerlegen Sie dessen Gültigkeit mittels TC1. Sollte das Argument nicht gültig sein, dann extrahieren Sie ein Gegenbeispiel aus dem Tableau. Geben Sie bitte die intendierte Bedeutung der benutzten Prädikaten- und Funktionssymbole an.

Alle Pflanzenfresser fressen Gras. Rinder fressen Gras. Daher sind Rinder Pflanzenfresser.

(6 Punkte)

Beispiel 1c

Überprüfen Sie, welche Eigenschaften auf die nachfolgend ausgeführten aussagenlogischen Formeln zutreffen und kreuzen Sie jeweils alle zutreffenden Eigenschaften an: (2 Punkte)

Multiple Choice-Quiz:

Pluspunkt für eine richtige Antwort:
Punkt für eine falsche Antwort:
Ignoriere die Fragen-Koeffizienten:

1 $(p\rightarrow q)\rightarrow (q\rightarrow p)$

	erfüllbar (satisfiable)
	widerlegbar (refutable)
	Tautologie (tautology)
	Kontradiktion (contradiction)

2 $(\neg p\land \neg q)\rightarrow (p\lor q)$

	erfüllbar (satisfiable)
	widerlegbar (refutable)
	Tautologie (tautology)
	Kontradiktion (contradiction)

3 $\neg ((p\land s)\rightarrow (q\lor r))\land (\neg q\land \neg s)$

	erfüllbar (satisfiable)
	widerlegbar (refutable)
	Tautologie (tautology)
	Kontradiktion (contradiction)

4 $(p\rightarrow (p\land q\land \neg q))\leftrightarrow \neg p$

	erfüllbar (satisfiable)
	widerlegbar (refutable)
	Tautologie (tautology)
	Kontradiktion (contradiction)

Beispiel 1d

Kreuzen Sie Zutreffendes an: (4 Punkte)

Multiple Choice-Quiz:

Pluspunkt für eine richtige Antwort:
Punkt für eine falsche Antwort:
Ignoriere die Fragen-Koeffizienten:

1 Für jede erfüllbare Aussage gibt es ein geschlossenes TC1-Tableau.

	richtig
	falsch

2 Für eine PL1-Formel $\varphi$ gilt in einer Interpretation $I$ entweder $I\vDash \varphi$ oder $I\vDash \neg \varphi$

	richtig
	falsch

3 TC1 terminiert immer.

	richtig
	falsch

4 $F\cup \{\varphi \}\vDash \neg \psi$ genau dann, wenn $F\cup \{\psi \}\vDash \neg \varphi$. (Antwort unkorrigiert)

	richtig
	falsch

5 Eine Formel ist genau dann erfüllbar wenn ihre Negation nicht gültig ist.

	richtig
	falsch

6 $\forall x(P(x)\lor Q(x))\vDash \forall xP(x)\lor \forall xQ(x)$

	richtig
	falsch

7 TC1 kann für jede Formel ein Modell erzeugen.

	richtig
	falsch

8 Ist $\varphi$ unerfüllbar, so ist $\exists x(\varphi \rightarrow \psi )\rightarrow \forall x(\varphi \rightarrow \psi )$ gültig für beliebiges $\psi$.

	richtig
	falsch

Beispiel 2: Nichtmonotones Schließen

Beispiel 2a

Gegeben seien folgende Defaults: $\Delta =\{{\frac {P(x):\neg Q(x)}{\neg Q(x)}},{\frac {Q(x):P(x),R(a)}{P(x)}},{\frac {\top :\neg P(x),\neg R(x)}{P(x)\land Q(x)}}\}$

$W_{1}=\{Q(a),R(b)\},E_{1}=Cn(W_{1})$

$W_{2}=\{P(a),\neg R(a)\},E_{2}=Cn(W_{2}\cup \{\neg Q(a)\})$

$W_{3}=\{R(a)\},E_{3}=Cn(W_{3})$

1) Geben Sie die klassischen Redukte $\Delta ^{E_{i}}$ von $\Delta$ bezüglich den Mengen $E_{i}$ an, für $i=1,2,3$.

2) Kreuzen Sie die korrekten Aussagen an: (6 Punkte)

Multiple Choice-Quiz Sub-Beispiel 2:

Pluspunkt für eine richtige Antwort:
Punkt für eine falsche Antwort:
Ignoriere die Fragen-Koeffizienten:

1 $E_{1}$ ist eine Extension der Default Theorie $T_{1}=\langle W_{1},\Delta \rangle$. (Antwort unkorrigiert)

	richtig
	falsch

2 $E_{2}$ ist eine Extension der Default Theorie $T_{2}=\langle W_{2},\Delta \rangle$.

	richtig
	falsch

3 $E_{3}$ ist eine Extension der Default Theorie $T_{3}=\langle W_{3},\Delta \rangle$. (Antwort unkorrigiert)

	richtig
	falsch

Anmerkung: Im Widerspruch zu Antwort 2 des MC Quiz, ist meiner Ansicht nach keiner der Kandidaten eine Extension. Um das zu überprüfen habe ich neben dem händischen Überprüfen die Default Theory in ein DLV Programm umgewandelt uns das Answer Set gecheckt.

Anmerkung zu vorheriger Anmerkung:

Würde ich nicht so sehen. Der einzige Default der zu der Menge von Redukten hinzugefügt werden kann ist ${\frac {P(a):\neg Q(a)}{\neg Q(a)}}$. Im nächsten Schritt wird dann überprüft ob die prerequisite P(a) aus der Wissensbasis hergeleitet werden kann, was der Fall ist. Daher kann $\neg Q(a)$ hinzugefügt werden. Schlussendlich stimmt der potenzielle Extension Kandidat mit der erzeugten Extension überein.

Beispiel 2b

Was ist ein normaler Default? Was ist eine normale Default Theorie? Welche Eigenschaft gilt für normale Default Theorien, jedoch im Allgemeinen nicht für beliebige? (2 Punkte)

Beispiel 2c

1) Geben Sie die formale Definition der Close-World Assumption CWA(T) einer Theorie T an.

2) Gegeben sei nun folgendes Wissensbasis $T$ über eine Sprache mit Konstantensymbolen $a,b$ und $c$, dem Variablensymbol $x$ und den Prädikatensymbolen $P$ und $Q$:

$T=\{P(a)\lor Q(a),\neg Q(b),P(c),\forall x(P(x)\rightarrow Q(x))\}$.

Geben Sie die $T_{asm}$ und CWA(T) an, indem Sie folgende Gleichungen ergänzen:

$T_{asm}=\{...\},CWA(T)=...$.

3) Welche der folgenden Eigenschaften treffen zu? (4 Punkte)

Multiple Choice-Quiz Sub-Beispiel 3:

Pluspunkt für eine richtige Antwort:
Punkt für eine falsche Antwort:
Ignoriere die Fragen-Koeffizienten:

1 T ist deduktiv abgeschlossen.

	richtig
	falsch

2 CWA(T) ist konsistent.

	richtig
	falsch

Beispiel 2d

Beweisen oder widerlegen Sie:

$Cn(T_{1})\cup Cn(T_{2})\subseteq Cn(T_{1}\cup T_{2})$. (4 Punkte)

Beispiel 3: Answer-Set Programming

Beispiel 3a

Erklären Sie das Guess-and-Check Paradigma der Answer-Set Programmierung anhand eines Programmes, welche alle Independent Sets eines Graphen berechnet.

Beachte: Sei $G=\langle V,E\rangle$ ein Graph, wobei V die Menge der Knoten und E die Menge der Kanten des Graphen sei. Ein Independent Set ist eine Teilmenge S der Knotenmenge V sodass keine Knoten in S benachbart (d.h. durch eine Kante verbunden) sind. Ein Independent Set ist also eine Menge $S\subseteq V$ sodass für alle $u,v\in S$ gilt, dass $u,v\notin E$. (6 Punkte)

Beispiel 3b

Was versteht man (i) unter einem abduktiven Diagnoseproblem und (ii) einer abduktiven Diagnose eines abduktiven Diagnoseproblems? (3 Punkte)

Beispiel 3c

Sei M eine Interpretation und P ein grundiertes logisches Programm.

(i) Definieren Sie den Begriff des Redukts $P^{M}$.

(ii) Wann ist M ein Answer Set von P? (4 Punkte)

Beispiel 3d

Welche der folgenden Aussagen aus dem Bereich von ASP treffen zu? (3 Punkte)

Multiple Choice-Quiz:

Pluspunkt für eine richtige Antwort:
Punkt für eine falsche Antwort:
Ignoriere die Fragen-Koeffizienten:

1 Falls eine Query unter Cautious Reasoning wahr ist, dann ist sie auch unter Brave Reasoning wahr. (Antwort unkorrigiert)

	richtig
	falsch

2 Wenn $M_{1}$ ein Answer Set eines Programms $P_{1}$ ist, und $M_{2}$ ein Answer Set eines Programms $P_{2}$, dann ist $M_{1}\cup M_{2}$ ein Answer Set von $P_{1}\cup P_{2}$. (Antwort umkorrigiert)

	richtig
	falsch

3 Ein Programm ohne Constraints hat immer mindestens ein Answer Set.

	richtig
	falsch

Beispiel 4: Probabilistisches Schließen

Beispiel 4a

In der allgemeinen Bevölkerung haben 1 von 25.000 Menschen die Krankheit X. Ein Test ergibt bei erkrankten Personen in 950 von 1.000 Fällen true. Bei gesunden Personen meldet der Test fälschlicherweise bei 10 von 1.000 Fällen true.

Bestimmen Sie $P(X=true|Test=true)$.

Hinweis: Der konkrete numerische Wert muss nicht explizit berechnet werden; es genügt die Angabe der Formel mit den entsprechenden Werten. (6 Punkte)

Beispiel 4b

Welche Eigenschaften haben atomare Ereignisse? Welche Arten von Zufallsvariablen gibt es? Genen Sie Erklärungen an! (3 Punkte)

Beispiel 4c

Leiten sie das Bayes'sche Gesetz aus der Produktregel her. (4 Punkte)

Beispiel 4d

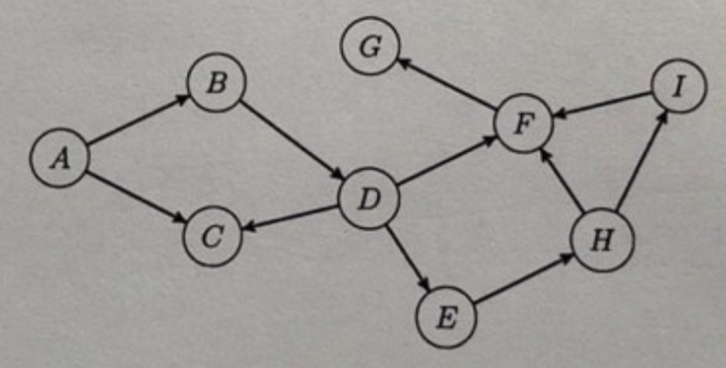
Gegeben ist folgender Graph eines Bayes'schen Netzes:

Welche der folgenden Eigenschaften folgen aus der Netzwerkstruktur? (3 Punkte)

Multiple Choice-Quiz:

Pluspunkt für eine richtige Antwort:
Punkt für eine falsche Antwort:
Ignoriere die Fragen-Koeffizienten:

1 A ist bedingt unabhängig von D bei Evidenz B und C.

	richtig
	falsch

2 A ist bedingt unabhängig von I bei Evidenz B und F. (Antwort fehlt am Scan, Begründung siehe Lösungsvorschlag)

	richtig
	falsch

3 C ist bedingt unabhängig von G bei Evidenz A und H. (Antwort fehlt am Scan, Begründung siehe Lösungsvorschlag)

	richtig
	falsch

Lösungsvorschläge:

• Lösungsvorschlag:
  • Frage (i) ist laut Korrektur am Scan falsch. Es gibt nur zwei ungerichtete Pfade von A zu D: A -> B -> D ist geblockt, da B eine eingehende und eine ausgehende Kante besitzt und in der Evidenz ist. A -> C <- D ist nicht geblockt, da C zwei eingehende Kanten besitzt aber in der Evidenz liegt. Da für bedingte Unabhängigkeit alle Pfade geblockt sein müssen ist A nicht bedingt unabhängig von D bei Evidenz B und C.
  • Frage (ii) wurde nicht korrigiert, ist meiner Meinung nach richtig. Jeder ungerichtete Pfad muss entweder den Streckenzug A -> B -> D oder A -> C <- D enthalten. A -> B -> D ist blockiert da B eine ein- und eine ausgehende Kante hat und in der Evidenz ist; A -> C <- D ist blockiert da C zwei eingehende Kanten hat und weder der Knoten noch nachfolgende (von denen es keine gibt) in der Evidenz liegen. Somit sind automatisch alle möglichen angerichteten Pfade blockiert.
  • Frage (iii) wurde nicht korrigiert, ist meiner Meinung nach falsch: Der Pfad C <- D -> F -> G ist nicht blockiert, für bedingte Unabhängigkeit müssen jedoch alle Pfade blockiert sein. (Andere mögliche Pfade sind blockiert da sie jedenfalls entweder über A (blockiert weil zwei ausgehende Kanten am Pfad und in Evidenz) oder H (blockiert weil eine ein- und eine ausgehende Kante und in Evidenz) führen, es gibt also nur einen nicht-blockierten Pfad.)

Materialien

Neues Material hinzufügen

E

• EWBS-Pruefung-2019-01-08-4d.jpeg (details)