Gegeben ist eine Ebene im Raum durch die folgende Gleichung:

Sei  eine Abbildung, die Punkte in Richtung normal auf die Ebene um den Faktor 8 skaliert. Die Punkte auf der Ebene selbst bleiben also fix.
eine Abbildung, die Punkte in Richtung normal auf die Ebene um den Faktor 8 skaliert. Die Punkte auf der Ebene selbst bleiben also fix.
Stellen Sie  dar in der Form
dar in der Form  mit
mit  und
und  .
.
Oft ist es sinnvoll Ebene in hessesche Normalform auszudrücken, also:

Hier also dann:

 (also nicht vergessen auch das
(also nicht vergessen auch das  dividieren)
dividieren)
Wir wollen, dass der Abstand von einem neuen Punkt in der Ebene 8-mal so groß ist wie der Abstand vom bestehenden Punkt zu der Ebene, d.h. wir müssen uns 7-mal von dem Punkt bewegen, also  (-, weil + wäre in dem Fall auf der anderen Seite der Ebene)
(-, weil + wäre in dem Fall auf der anderen Seite der Ebene)
Es wird jetzt ähnlich zu dem "Kochrezept" (PDF) vorgegangen wo es um das um das Spiegeln geht.

Einsetzen:

Jedes Skalarprodukt kann auch als Matrixprodukt dargestellt werden indem man den ersten Vektor transponiert und dann eine Matrixmultiplikation durchführt.


In der Ebene ist die Gerade  in Normalform gegeben. Seien weiters
in Normalform gegeben. Seien weiters  und
und  zwei Punkte, die nicht auf der Geraden liegen.
zwei Punkte, die nicht auf der Geraden liegen.
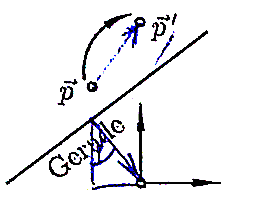
Gesucht ist eine Affinität  , die die Punkte auf der Geraden fest lässt, und
, die die Punkte auf der Geraden fest lässt, und  auf
auf  abbildet.
abbildet.
Hinweis: Bestimmen Sie zuerst  , indem Sie das Problem durch eine Translation so tranformieren, dass die Gerade durch den Ursprung geht.
, indem Sie das Problem durch eine Translation so tranformieren, dass die Gerade durch den Ursprung geht.
Gegeben sei eine Ebene im Raum und eine auf sie normale Gerade. Gesucht ist die Menge aller Punkte, die von der Geraden denselben Abstand wie von der Ebene.
Vereinfachen Sie die Aufgabe o.B.d.A., indem Sie Ebene und Gerade so ins Koordinatensystem legen, dass sie möglichst einfach dargestellt werden.
Was für eine Art von Fläche ergibt sich?
o.B.d.A kann die Ebene so gedreht und ausgerichtet werden das sie in der X-Y Ebene liegt.
Weiters sollte sie so verschoben werden das die Gerade welche Normal auf zur Eben steht durch den Nullpunkt geht.
Daraus folgt:
Normierter Richtungsvektor der Geraden und Normale der Ebene sind beide 
(Nachfolgende Abstandsberechnungen gehen davon aus das  ist. Ist in diesem Fall gegen.)
ist. Ist in diesem Fall gegen.)
Der Abstand eines Punktes  zu einer Ebene, welche durch den Ursprung geht, ist gegeben durch
zu einer Ebene, welche durch den Ursprung geht, ist gegeben durch 
Der Abstand eines Punktes  zu einer Geraden, welche durch den Ursprung geht, ist gegeben durch
zu einer Geraden, welche durch den Ursprung geht, ist gegeben durch 
Da  auch negativ sein kann (Punkt befindet sich auf der Rückseite der Ebene) und sich
auch negativ sein kann (Punkt befindet sich auf der Rückseite der Ebene) und sich  leicht umformen lässt, ist es von Vorteil wenn wir beide Abstandsmaße quadrieren.
leicht umformen lässt, ist es von Vorteil wenn wir beide Abstandsmaße quadrieren.
Somit folgt: 
wobei: 
Somit folgt: 
jetzt setzen wir für  und
und  ein.
ein.
Somit folgt: 
Somit folgt: 
Somit folgt: 
Die Art der Fläche die entsteht ist ein Doppelkegel. (Spitze im Schnittpunkt: (Gerade / Ebene) und Ausrichtung: (Entlang der Normalen der Ebene))
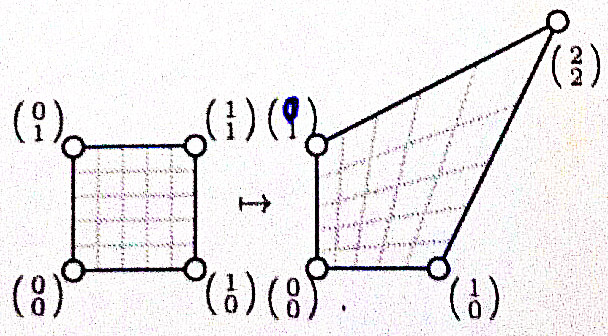
Bestimmen Sie eine Matrix  einer Kollineation, die das Vierreck links in das Vierreck rechts überführt. D.h.
einer Kollineation, die das Vierreck links in das Vierreck rechts überführt. D.h.  ,
, and
and  .
.
Hinweis: Bestimmten Sie zuerst, worauf die Fernpunkte  und
und  abgebildet werden müssen; zusammen mit dem Bild von
abgebildet werden müssen; zusammen mit dem Bild von  bestimmt das die Spalten von
bestimmt das die Spalten von  bis auf Faktoren; diese Faktoren müssen so sein, dass der vierte Punkt des Vierecks korrekt abgebildet wird.
bis auf Faktoren; diese Faktoren müssen so sein, dass der vierte Punkt des Vierecks korrekt abgebildet wird.
Ein Punkt im 
 kann homogen erweitert und dadruch in den
kann homogen erweitert und dadruch in den  gebracht werden. der neue Punkt hat dann die Form
gebracht werden. der neue Punkt hat dann die Form  wobei
wobei  ein frei wählbar Skalar
ein frei wählbar Skalar  ist.
ist.
Alle Homogenen Koordinaten, können, aufgrund wie sie definiert sind, immer mit einem bliebenFaktor  mutipliziert werden.
mutipliziert werden.
Eine Transformationsmatrix jeder Art bildet immer die Einheitsvektoren auf die Vektoren in der Matrix ab. z.B.: im Fall von 

Was wir jetzt wissen wollen, um das Beispiel zu Lösen, ist, worauf muss die Matrix  Abgebildet werden.
Abgebildet werden.
Wenn man sich jetzt die Bedeutung der Einheitsvektoren nun genauer ansieht,ist die gesuchte Lösung relativ einfach zu finden.
Der erste Einheitsvektor  ist der "Schnittpunkt" ak. Fernpunkt aller Geraden die zur X-Achse parallel sind.
ist der "Schnittpunkt" ak. Fernpunkt aller Geraden die zur X-Achse parallel sind.
Der zweite Einheitsvektor  ist der "Schnittpunkt" ak. Fernpunkt aller Geraden die zur Y-Achse parallel sind.
ist der "Schnittpunkt" ak. Fernpunkt aller Geraden die zur Y-Achse parallel sind.
Der dritte Einheitsvektor  ist der 0 Punkt in homogenen Koordinaten.
ist der 0 Punkt in homogenen Koordinaten.
Somit stellt sich nun die Frage wohin werden diese Punkte abgebildet.
Bei gegeben Beispiel schneiden sich nun die Geraden, welche zuvor parallel wahren jetzt in eigentlichen Punkten, und der Ursprung, ist nach wie vor am 0 Punkt (also nicht verschoben).
Der neue "Schnittpunkt" aller Geraden welche einst zur X-Achse parallel wahren ist nun 
Der neue "Schnittpunkt" aller Geraden welche einst zur Y-Achse parallel wahren ist nun 
Der neue Ursprung ist nun 
Nachdem man diese Koordinaten nun homogen erweitert. erhält man:



Also in Matrixschreibweise 
Jetzt muss man nur noch einen Punkt und dessen Abbild einsetzten um konkrete Werte für die  zu bestimmen. Hierbei ist zu beachten das keine Punkte gewählt werden darf welcher ursprünglich auf eine oder mehren Achsen lag.
zu bestimmen. Hierbei ist zu beachten das keine Punkte gewählt werden darf welcher ursprünglich auf eine oder mehren Achsen lag.
In unserem Fall ist es der Punkt  welcher auf
welcher auf  abgebildet wird.
abgebildet wird.
Nach Homogenisieren der Punkte erhalten wir nun folgen Gleichung:
(Anmerkung: Auf die  wurde in diesem Schritt verzichtet bzw. wurde als 1 gewählt -> so erhält man eine konkrete Matrix und keine relativen Werte)
wurde in diesem Schritt verzichtet bzw. wurde als 1 gewählt -> so erhält man eine konkrete Matrix und keine relativen Werte)

Somit folgt:



Die gesuchte Matrix  ist also
ist also 

