TU Wien:Algebra und Diskrete Mathematik VU (diverse)/Übungen 2023W/Beispiel 46

Man beschreibe die Menge jener komplexen Zahlen z, die $\Re ({\frac {z-a}{b}})>0$ erfüllen ($a,b\in \mathbb {C} ,$ b != 0), graphisch

Dieses Beispiel ist als solved markiert. Ist dies falsch oder ungenau? Aktualisiere den Lösungsstatus (Details: Vorlage:Beispiel)

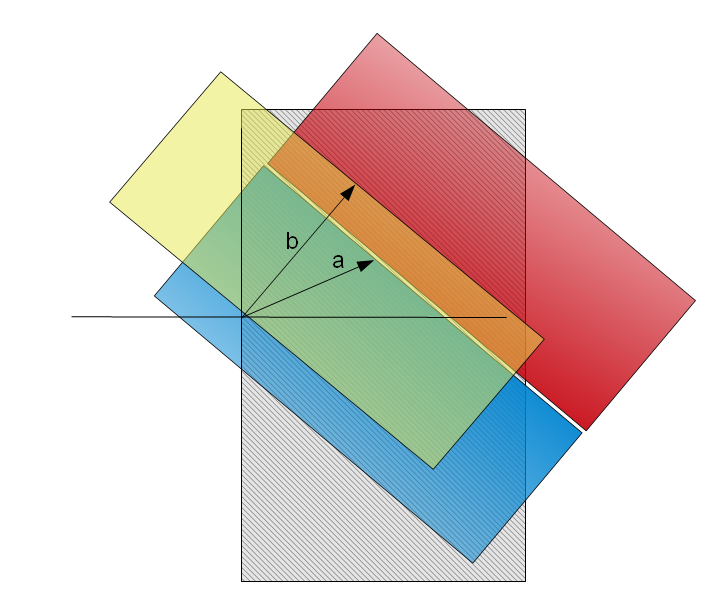
Ich hab eine Skizze angefertigt, um das Verständnis zu wecken. Das Ergebnis ist eine verschobene Halbebene (Rot markiert).

Erläuterung der Grafik:

Die Werte a,b sind als Vektoren eingezeichnet (ihre Interpretation in der Gauß'schen Zahlenebene). Die Grau schraffierte Fläche entspricht allen Werten wo $\Re ({z})>0$. Der entgegengesetzte Teil entspricht natürlich $\Re ({z})<0$. Diese Halbebene wird durch die Divsion durch b um den Winken von b gedreht (gelbe Halbebene). Abschließend ist noch durch die Subtraktion eine Verschiebung dieser Halbebene vorgegeben, nämlich genau um a. Das Ergebnis von $\Re ({\frac {z-a}{b}})>0$ ist somit die rote Halbebene. Ebenfalls noch eingezeichnet $\Re ({\frac {z-a}{b}})<0$ als Blaue Halbebene.

Man vergleiche die Analogie zu Bsp. 43.

--W1n5t0n 14:11, 14. Jun. 2009 (CEST)