TU Wien:Mathematik 1 UE (diverse)/Übungen SS09/Beispiel 43

Man beschreibe die Menge jener komplexen Zahlen z, die $\Im ({\frac {z-a}{b}})>0$ erfüllen ($a,b\in \mathbb {C} ,b\neq 0$)

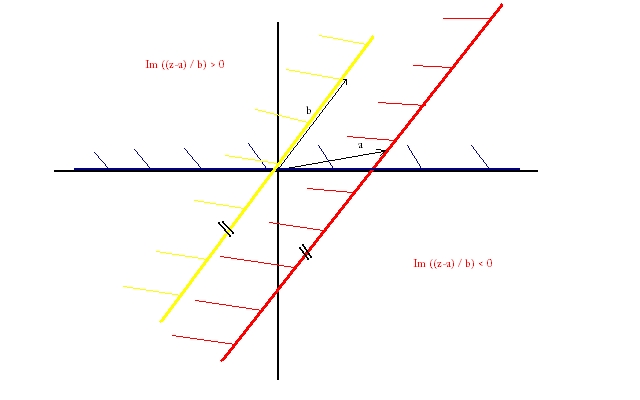
Ich hab eine Skizze angefertigt, um das Verständnis zu wecken. Das Ergebnis ist eine verschobene Halbebene (Rot markiert).

Die entgegengesetzte Halbebene entspricht allen $\Im ({\frac {z-a}{b}})<0$

Man muss das Beispiel sich folgendermaßen überlegen:

1. Schritt

Die Blau markierte Halbfläche beschreibt alle z, deren Imaginärteil > 0 ist, also im I. oder II. Quadranten liegen (oberhalb der X-Achse). Isoliert betrachtet alle $Im(z)>0$.

Die Division durch eine komplexe Zahl, ist eine Stauchung, und eine Drehung. Die Stauchung interessiert uns im Moment nicht, die Drehung ist aber entscheidend. Da bei der Division der Winkel von b ($\phi (b)$) abgezogen wird, müssen wir ihn entsprechend dazu addieren, und erhalten von der blauen Halbebene die gelbe Halbebene.

2. Schritt

Nun wird ein Vektor a abgezogen, in der anderen Reihenfolge gesprochen, dazu addiert. Das Resultat ist eine Parallelverschiebung um a. Und somit erhalten wir die rot gekennzeichnete Halbebene.

Schlussfolgerung

Bildlich gesprochen sind nun also alle z, die in der roten Halbebene liegen in der geforderten Menge enthalten. q.e.d.

-- W1n5t0n 18:30, 23. Mär. 2009 (CET)