TU Wien:Mathematik 1 UE (diverse)/Übungen SS10/Beispiel 30

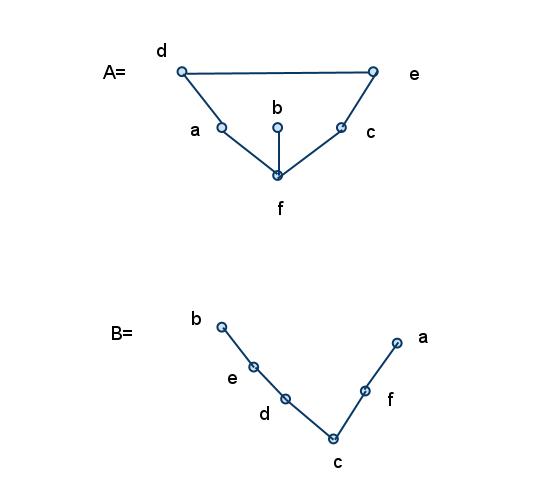
Welche der nachstehenden Adjazenzmatrizen stellen einen Baum dar?

$A={\begin{pmatrix}0&0&0&1&0&1\\0&0&0&0&0&1\\0&0&0&0&1&1\\1&0&0&0&1&0\\0&0&1&1&0&0\\1&1&1&0&0&0\end{pmatrix}}$, $B={\begin{pmatrix}0&0&0&0&0&1\\0&0&0&0&1&0\\0&0&0&1&0&1\\0&0&1&0&1&0\\0&1&0&1&0&0\\1&0&1&0&0&0\end{pmatrix}}$

Lösungsvorschlag

By Chameleon

Diagramm (mehrere Lösungen möglich)

A ist zwar zusammenhängend ist aber dennoch kein Baum weil ein Kreis existiert durch die Verbindung (d,e).

B ist ein Baum weil alle Knoten verbunden sind und kein Kreis existiert.

Lösungsvorschlag

By Juggl3r

Es gibt noch eine andere Möglichkeit: Aber Achtung, hier wird nicht überprüft, ob das Graph zusammenhängend ist. D.h. dies müsste extra noch gemacht werden! Ein Graph ist genau dann ein Baum, wenn er bei n Knoten (n-1) Kanten hat. Das heißt, wir können in der Adjazenzmatrize die 1er in den Spalten zählen (bzw. oder in den Zeilen, es ist beides hier möglich) und erhalten somit den Grad des jeweiligen Knotens. Summieren wir alle Grade auf, so erhalten wir 2*Anzahl der Kanten und das muss (n-1) sein. In der Matrix A haben wir 6 Knoten (a bis f):

deg(a) = 2

deg(b) = 1

deg(c) = 2

deg(d) = 2

deg(e) = 2

deg(f) = 3

Summe = 12

Anzahl der Kanten = 12/2 = 6.

Die Anzahl der Kanten müsste aber (6-1) = 5 sein, daher kein Baum.

In der Matrix B haben wir 6 Knoten (a bis f):

deg(a) = 1

deg(b) = 1

deg(c) = 2

deg(d) = 2

deg(e) = 2

deg(f) = 2

Summe = 10

Anzahl der Kanten = 10/2 = 5.

Die Anzahl der Kanten muss (n-1) = (6-1) = 5 sein und das ist sie auch. => Baum