TU Wien:Mathematik 1 UE (diverse)/Übungen WS06/Beispiel 132

Man bestimme für das "6 aus 45"-Lotto die Anzahl der möglichen Fünfer mit Zusatzzahl (d.h. die Anzahl derjenigen 6-elementigen Teilmengen von {1,2,..,45}, die mit einer vorgegebenen 6-elementigen Teilmenge genau 5 Elemente gemeinsam haben und deren sechstes Element einen vorgegebenen Wert außerhalb der 6-elementigen Menge hat).

Lösungsvorschlag von mnemetz

Allgemeines zu 6 aus 45

(Grafiken wurden von mir erstellt --Mnemetz 16:29, 25. Nov 2005 (CET))

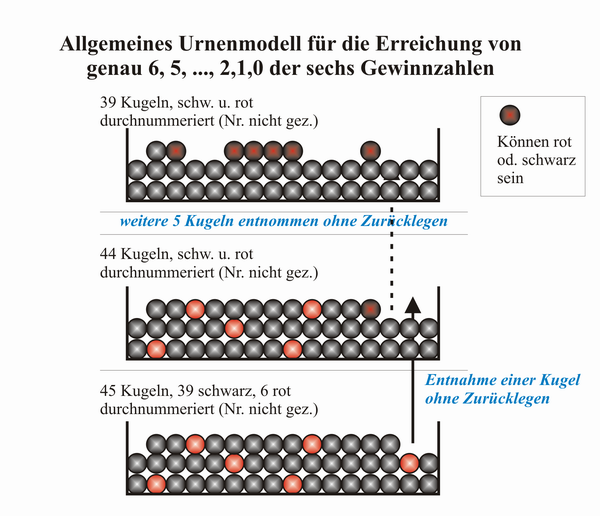
Es ist hilfreich, dass sog. Urnenmodell zum besseren Verständnis zu bemühen.

In einer Urne befinden sich 45 Kugeln, die von 1 bis 45 nummeriert sind. Davon sind sechs Kugeln rot, und zwar jene Kugeln, deren Nummern die Tippreihe des Spielers bilden. Die übrigen 39 Kugeln sind schwarz. Aus dieser Urne werden sechs Kugeln ohne Zurücklegen gezogen.

„6 Richtige“ hat der Spieler genau dann, wenn bei sechsmaligem Ziehen ohne Zurücklegen sechs rote Kugeln gezogen werden.

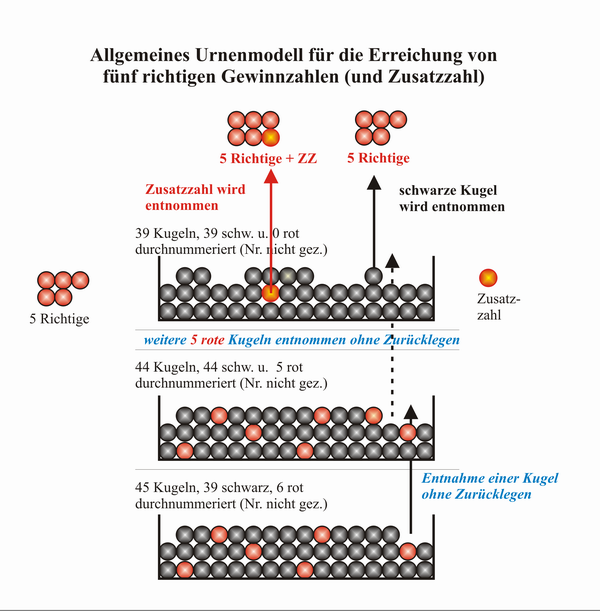
Folgende Grafik verdeutlicht die Situation des Fünfers mit Zusatzzahl:

Berechnung der Möglichkeiten des 5ers mit ZZ

Es ist klar, dass die Auswahlmenge A {1,2,3, ... ,45} umfasst. Es werden zunächst sechs Zahlen aus dieser vorgegeben. Somit ist die Anzahl der möglichen Tipps mit ${\begin{pmatrix}45\\6\end{pmatrix}}$ definiert. (8145060)

Es liegt eine Kombination vor. Darunter versteht man ein ungeordnetes k-Tupel {$a_{1},...,a_{k}$} verschiedener Elemente von A, oder eine k-elementige Teilmenge von A.

Betrachten wir wieder die Urne mit den von 1 bis 45 nummerierten Kugeln, von denen 6 Kugeln rot und die übrigen 39 Kugeln schwarz sind. Insgesamt gibt es ${\begin{pmatrix}45\\6\end{pmatrix}}$ Möglichkeiten, aus dieser Urne sechs Kugeln ohne Zurücklegen zu ziehen (= "Kombination ohne Wiederholung"). „k Richtige“ (0  k  6) hat man dann, wenn dabei k rote Kugeln und 6-k schwarze gezogen werden. Es gibt ${\begin{pmatrix}6\\k\end{pmatrix}}$ Möglichkeiten, k von 6 roten Kugeln auszuwählen, und ${\begin{pmatrix}39\\6-k\end{pmatrix}}$ Möglichkeiten, die restlichen 6-k Kugeln aus den 39 schwarzen Kugeln auszuwählen. Insgesamt gibt es daher Möglichkeiten, k rote und 6-k schwarze Kugeln zu ziehen. Daraus folgt, dass die Anzahl der Gewinnmöglichkeiten abhängig von k beträgt:

${\begin{pmatrix}6\\k\end{pmatrix}}{\begin{pmatrix}39\\6-k\end{pmatrix}}$

Obenstehende Formel basiert auf einer Kombination ohne Wiederholungen.

Für die Berechnung der Anzahl von "5 Richtigen mit Zusatzzahl" wird wie folgt vorgegangen: Es wird ${\begin{pmatrix}6\\5\end{pmatrix}}$ (die Anzahl der Möglichkeiten von 5 Richtigen aus 6 möglichen Richtigen) mit ${\begin{pmatrix}1\\0\end{pmatrix}}$ (nämlich gerade "0 Richtige" aus der Anzahl der Möglichkeiten von 1 richtigen Zusatzzahl) und mit ${\begin{pmatrix}39\\0\end{pmatrix}}$ (nämlich gerade 1 Kugel aus den restlichen verbleibenden 39 Kugeln) multipliziert.

${\begin{pmatrix}6\\5\end{pmatrix}}{\begin{pmatrix}1\\0\end{pmatrix}}{\begin{pmatrix}38\\1\end{pmatrix}}=228$

Die Berechnung für die Anzahl der Möglichkeiten für "5 Richtige mit Zusatzzahl" ist dann gerade:

${\begin{pmatrix}6\\5\end{pmatrix}}{\begin{pmatrix}1\\1\end{pmatrix}}{\begin{pmatrix}38\\0\end{pmatrix}}=6$

Hat der Spieler nach Ziehen der sechs Gewinnzahlen genau fünf Richtige, so sind aus der betrachteten Urne fünf rote und eine schwarze Kugel gezogen worden. Somit liegen noch eine rote und 38 schwarze Kugeln in der Urne. Diese eine rote Kugel ist die Zusatzzahl. Sie reduziert die Möglichkeiten der Kombinationen drastisch.

Das ganze kann man auch einfach nachvollziehen, indem man sich überlegt, aus welchen "Komponenten" der 5er mit ZZ eigentlich besteht: Aus den 6 Gewinnzahlen beinhaltet er 5 sowie eine Niete. Eine weitere Gewinnzahl kann dann aus den verbleibenden 39 gezogen werden - EINE. Alles weitere ergibt sich dann logisch.

Hilfreiches

• https://web.archive.org/web/*/http://www.mathe-online.at/materialien/maria.koth/files/allerlei/Lotto.DOC (!)
• https://web.archive.org/web/20180817160209/https://www.hausarbeiten.de/de/catalog/subject/197 (!)
• https://web.archive.org/web/20180817160214/https://www.mathe-online.at/materialien/Daniela.Eder/files/Diskrete_WK/Zusammenstellung.html
• Google Groups Eintrag
• Google Groups Eintrag 2