TU Wien:Mathematik 1 UE (diverse)/Übungen WS06/Beispiel 149

Angabe

Ein Turm soll auf einem Schachbrett vin der linken unteren Ecke in die rechte obere Ecke ziehen. Wieviel verschiedene Wege gibt es, wenn der Turm nie nach links oder nach unen ziehen darf, d.h. bei jedem Schritt nur ein oder mehrere Felder nach rechts oder nach oben?

Lösungsvorschlag von mnemetz

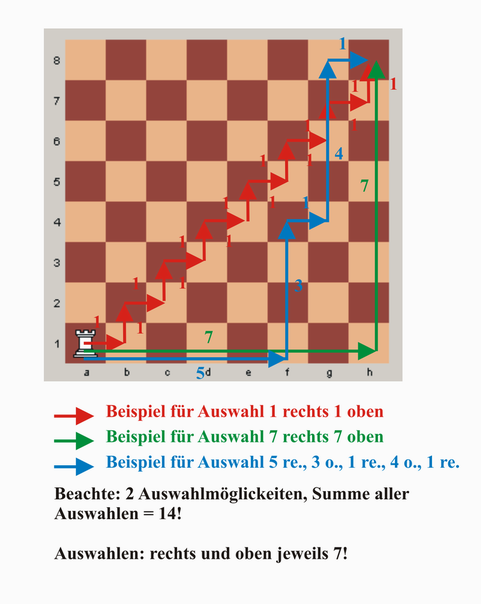
Eine Grafik zur Veranschaulichung:

Wir stellen fest, dass

• der Turm immer zwei Möglichkeiten hat wohin er ziehen kann (rechts, oben)
• der Turm mindestens 1 Feld nach rechts ziehen kann und maximal 7 (analog nach oben)
• bedingt durch die Einschränkung des Schachbrettes können max. 7 Züge nach rechts und ebensoviele max. nach oben ausgeführt werden
• die Summe der o.g. Maxima ist 14

Man kann die möglichen Zugkombinationen als Permutation mit Wiederholung anschreiben.

${\frac {14!}{7!*7!}}=3432$ Kombinationen.

Eine zweite Anschauung:

• ein Move des Turms besteht darin, dass er GENAU 1 Feld entweder nach rechts oder nach oben zieht.
• Damit der Turm vom linken unteren Eck zum rechten oberen kommt muss er GENAU 7x NACH RECHTS UND 7x NACH OBEN FAHREN, wobei es egal ist, in welcher Reihenfolge das geschieht.

zwei Möglichkeiten für eine gültige Sequenz an Turmzügen lauten (O=oben, R=rechts)

1) O O O O O O O R R R R R R R

2) O R O R O R O R O R O R O R (7x O und 7x R, die Gesamtzahl der Züge beträgt somit 14)

Die Anzahl an unterschiedlichen Möglichkeiten durch Vertauschung von O's und R's würde 14! betragen, wenn die O's und R's unter sich UNTERSCHEIDBAR wären. Das sind sie aber nicht, deshalb muss die Anzahl der Möglichkeiten einmal wegen R durch 7! und einmal wegen O durch 7! dividiert werden. Soviele Möglichkeiten fallen nämlich auf EINE beliebige Zugsequenz, wenn sie unterscheidbar wären.