TU Wien:Mathematik 1 UE (diverse)/Übungen WS06/Beispiel 163

Angabe

Auf wieviele Arten können 8 Türme auf ein Schachbrett gestellt werden, derart, daß sie einander nicht schlagen und die weiße Diagonale freibleibt? (Ein Turm schlägt eine andere Figur, die horizontal oder vertikal auf gleicher Höhe steht, sofern keine andere Figur dazwischen steht.

(viel einfachere) Alternative

Die Anordnung der Türme ist, wie bereits erklärt eine Permutation. Man könnte es sich so vorstellen, dass die Türme am anfang alle genau auf der weißen Diagonale stehen. Nun will ich die Türme so umordnen, dass 1) keiner mehr auf seinem alten Platz steht (sprich auf der weißen Diagonale) und 2) keiner den anderen schlägt.

Das 1) ist gewährleistet, wenn ich nur die fixpunktfreien Permutationen betrachte, also $n!*\sum _{n=0}^{n=8}{\frac {(-1)^{n}}{n!}}$ (laut Mitschrift).

Das 2) ergibt sich automatisch, weil bei einer fixpunktfreien Permutation ja nicht Zwei elemente auf dem selben Platz umgeordnet werden können.

Veranschaulichung (von mnemetz

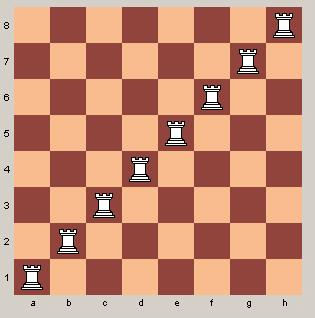
Ein Beispiel (weiße Hauptdiagonale unbesetzt!):

Lösungsvorschlag von der Lerngruppe vom 28.12.2005

Wir überlegten uns zuerst, wieviele Möglichkeiten es überhaupt gibt, die 8 Türme zu platzieren, so dass sie einander nicht schlagen können. (Die Einschränkung mit der Diagonale lassen wir mal beiseite!)

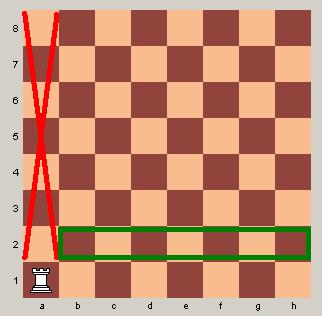
Möglichkeiten im Durchgang der einzelnen Reihen von 1-8 - zuerst ein grafisches Beispiel bei besetzter erster Reihe:

1. 8 Möglichkeiten zur Auswahl
2. 7 Möglichkeiten zur Auswahl
3. 6 Möglichkeiten zur Auswahl
4. 5 Möglichkeiten zur Auswahl
5. 4 Möglichkeiten zur Auswahl
6. 3 Möglichkeiten zur Auswahl
7. 2 Möglichkeiten zur Auswahl
8. 1 Möglichkeit zur Auswahl

Es handelt sich hier um eine Variation mit Wiederholung, und für diese gilt die Formel: ${\frac {n!}{(n-k)!}}$. Da aber n und k gleich 8 sind (8 Türme, 8 Reihen), liegt ein Spezialfall vor: die Permutation. Die Anzahl der Möglichkeiten, 8 Türme zu platzieren, beträgt somit $8!=40320$

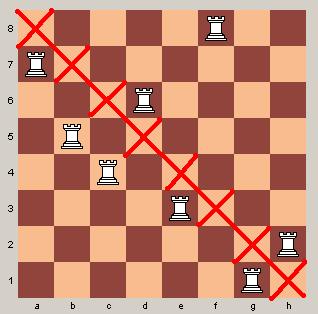
Nun gilt aber als Erschwernis, dass die weiße Diagonale zusätzlich nicht von Türmen besetzt werden darf - ein Beispiel:

Es handel sich hier um eine sog. fixpunktfreie Permutation, auch Derangement bezeichnet. Dies ist eine Permutation bei der kein einziges Element an seinem Platz bleibt.

Die Anzahl der möglichen Derangements einer Menge mit $n$ Elementen entspricht der Subfakultät $!n$: $d_{n}=!n=n!\cdot \sum _{i=0}^{n}{\left(-1\right)^{i} \over i!}$.

Somit lautet unsere Formel: $n!*\sum _{n=0}^{n=8}{\frac {-1^{n}}{n!}}$

Wir berechnen also:

$n!*(1-1+{\frac {1}{2!}}-{\frac {1}{3!}}+{\frac {1}{4!}}-{\frac {1}{5!}}+{\frac {1}{6!}}-{\frac {1}{7!}}+{\frac {1}{8!}})=40320*\approx 0.37=14833$

Es gibt somit 14.833 Möglichkeiten, die 8 Türme so zu platzieren, dass sie einander nicht schlagen können sowie die weiße Hauptdiagonale nicht betreten.

Edit: Rechenfehler, siehe: http://www.wolframalpha.com/input/?i=sum%288!*%28-1%29^k%2F%28k!%29%2Ck%2C0%2C8%29 (zuvor stand 14.883)

Anhang 1: Subfakultät (von mnemetz)

Die Subfakultät ist eine vornehmlich in dem mathematischen Gebiet der Kombinatorik auftretende Funktion. Die Subfakultät gibt die Anzahl der fixpunktfreien Permutationen (auch Derangements) auf einer endlichen Menge an. Sie ist eng mit der Fakultät verwandt, welche die Gesamtzahl der Permutationen auf einer endlichen Menge angibt.

formale Definition

Sei $n\in \mathbb {N} _{0}$ und $M:=\{1,2,\ldots ,n\}$. Eine Abbildung $\phi :M\rightarrow M$ heißt fixpunktfrei, wenn für alle $m\in M$ die Beziehung $\phi (m)\neq m$ gilt. Die Subfakultät von $n$ ist definiert als

$!n:=|\{\phi :M\rightarrow M\mid \phi {\mbox{ bijektiv und fixpunktfrei}}\}|$

Eine Formel für !n

Die Subfakultät kann mit Hilfe der Fakultät explizit berechnet werden. Es gilt:

$!n=n!\left(1-{\frac {1}{1!}}+{\frac {1}{2!}}-{\frac {1}{3!}}+...+(-1)^{n}{\frac {1}{n!}}\right)=n!\sum _{k=0}^{n}{\frac {(-1)^{k}}{k!}}$

Die ersten 11 Werte der Subfakultät sind !0 = 1, !1 = 0, !2 = 1, !3 = 2, !4 = 9, !5 = 44, !6 = 265, !7 = 1 854, !8 = 14.833, !9 = 133.496 und !10 = 1 334.961

Beispiel einer Anwendung

Angenommen man hat 6 verschiedenfarbige Kugeln, und zu jeder Kugel ein Kästchen in der passenden Farbe. Zu bestimmen ist die Anzahl der Möglichkeiten, die Kugeln so auf die Kästchen zu verteilen, dass jedes Kästchen genau eine Kugel enthält, aber keine Kugel in einem gleichfarbigen Kästchen zu liegen kommt.

Nach der Definition der Subfakultät gibt es genau $!6$ Möglichkeiten. Mit Hilfe der obigen Formel berechnet man $!6=6!\cdot \left(1-{\frac {1}{1!}}+{\frac {1}{2!}}-{\frac {1}{3!}}+{\frac {1}{4!}}-{\frac {1}{5!}}+{\frac {1}{6!}}\right)=265$.

Anhang 2: Schachtürme und Mathematik (von mnemetz)

Siehe PDF-Dokument (1,1MB) - einige Seiten aus J. Gik, Schach und Mathematik, Sportverlag Berlin 1986