TU Wien:Mathematik 1 UE (diverse)/Übungen WS06/Beispiel 164

Angabe

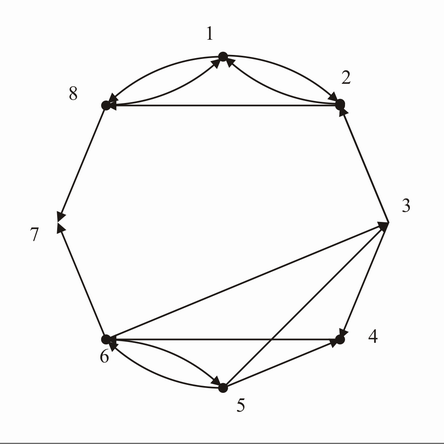
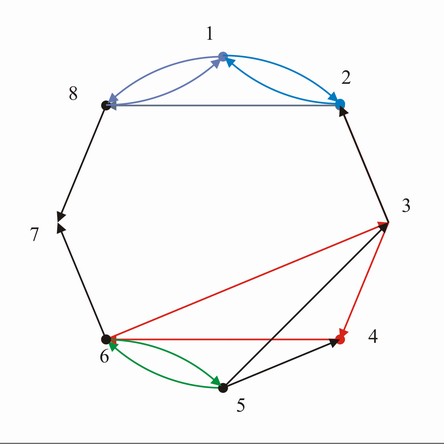
(a) In nachstehendem Graphen gebe man (verschiedene) Beispiele für eine gerichtete Kantenfolge, einen Kantenzug und einen Weg vom Knoten 6 zum Knoten 1 an.

(b) Desgleichen finde man eine geschlossene Kantenfolge, einen geschlossenen Kantenzug sowie einen Kreis jeweils durch den Knoten 5.

(c) Man zeige, dass G schwach, aber nicht stark zusammenhängend ist und bestimme die starken Zusammenhangskomponenten.

Theoretische Grundlagen (von mnemetz)

• Kantenfolge: Von einem Startpunkt ausgehend existiert ein Weg (über einen vorgegebenen Punkt) zum Startpunkt zurück. In einem gerichteten Graphen muss zusätzlich die Richtung übereinstimmen. <-- Diese Definition ist inkorrekt! Eine Kantenfolge ist eine Folge von Kanten die Knoten v und w miteinander verbindet, d.h. v, v1, v2, ... vk-1, w € V mit e1 = (v,v1), e2=(v1, v2), .. ek-1(vk-2, vk-1), ek = (vk-1,w). Nur, wenn die Kantenfolge auch geschlossen ist, müssen Anfangs- und Endknoten übereinstimmen. Ansonsten reicht es wenn zwischen v und w eine Kante liegt, dann ist w von v aus erreichbar.
• Kantenzug: Dies ist eine Kantenfolge, in der keine Kante mehrfach auftritt.
• Weg: Ist eine offene Kantenfolge, in der kein Knoten mehrfach auftritt.

Kantenfolge und Kantenzug können die Attribute offen oder geschlossen haben.

Lösungsvorschlag von mnemetz

(a)

(a) In nachstehendem Graphen gebe man (verschiedene) Beispiele für eine gerichtete Kantenfolge, einen Kantenzug und einen Weg vom Knoten 6 zum Knoten 1 an.

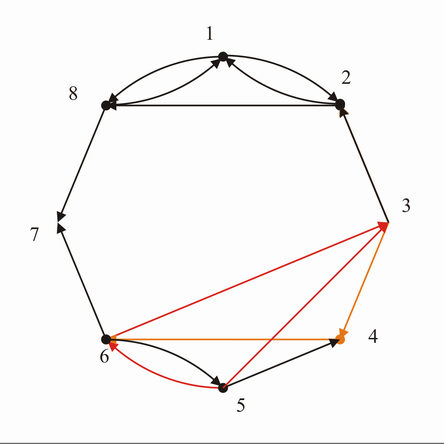
• gerichtete Kantenfolge (s. Grafik u.)
  • $6\Rightarrow 3\Rightarrow 5\Rightarrow 6$
  • $6\Rightarrow 3\Rightarrow 4\Rightarrow 6$

• Kantenzug
  • s. ger. Kantenfolge

• Weg 6->1 (s. Grafik u.)
  • $6\Rightarrow 3\Rightarrow 2\Rightarrow 1$
  • $6\Rightarrow 3\Rightarrow 2\Rightarrow 8\Rightarrow 1$
  • $6\Rightarrow 5\Rightarrow 3\Rightarrow 2\Rightarrow 1$
  • $6\Rightarrow 5\Rightarrow 3\Rightarrow 2\Rightarrow 8\Rightarrow 1$

(b)

Desgleichen finde man eine geschlossene Kantenfolge, einen geschlossenen Kantenzug sowie einen Kreis jeweils durch den Knoten 5.

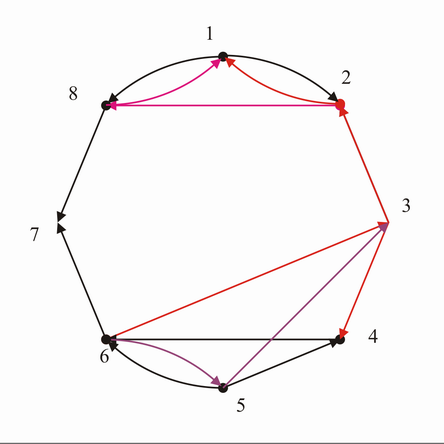
• Geschlossene Kantenfolge (s. Grafik u.)
  • $4\Rightarrow 6\Rightarrow 5\Rightarrow 4$
  • $3\Rightarrow 4\Rightarrow 6\Rightarrow 5\Rightarrow 3$

• geschlossener Kantenzug
  • s. geschl. Kantenfolge

• Kreis
  • s. geschl. Kantenfolge

(c)

Man zeige, dass G schwach, aber nicht stark zusammenhängend ist und bestimme die starken Zusammenhangskomponenten.

Graph ist nur schwach zusammenhängend, da keinesfalls von jedem Punkt aus der andere erreicht werden kann (Beispiele $8\Rightarrow 7$, $6\Rightarrow 7$, $3\Rightarrow 2$).

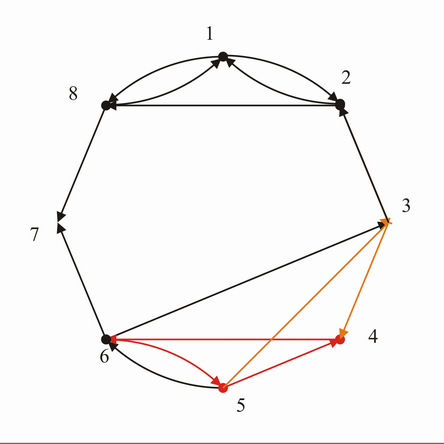
• Starke Zusammenhangskomponenten (s. Grafik u.)
  • $6\Rightarrow 5$
  • $1\Rightarrow 2$
  • $1\Rightarrow 8$
  • $2\Rightarrow 8\Rightarrow 1$
  • $3\Rightarrow 4\Rightarrow 6$

ACHTUNG: Laut Prof. Länger ist diese Lösung der starken Zusammenhangskomponenten nicht korrekt, da keine Knoten zu 2 starken Zusammenhangskomponenten gehören dürfen, sondern zu genau einer. Laut Prof. Länger sind die st. Zusammenhangskomponenten: {7}, {1,2,8}, {3,4,5,6}. (Man muss von jedem Knoten zu jedem anderen (auch wieder zum Startknoten zurück) kommen können)