TU Wien:Mathematik 1 UE (diverse)/Übungen WS06/Beispiel 172
Angabe[Bearbeiten | Quelltext bearbeiten]
Ein schlichter Graph heißt kubisch, wenn jeder Knoten Knotengrad d(v) = 3 hat.
a) Geben Sie ein Beispiel für einen kubischen Graphen mit an!
b) Gibt es einen kubischen Graphen mit ungerader Knotenanzahl ?
c) Zeigen Sie, daß es zu jedem einen kubischen Graphen mit gibt!
Lösungsvorschlag von mnemetz[Bearbeiten | Quelltext bearbeiten]
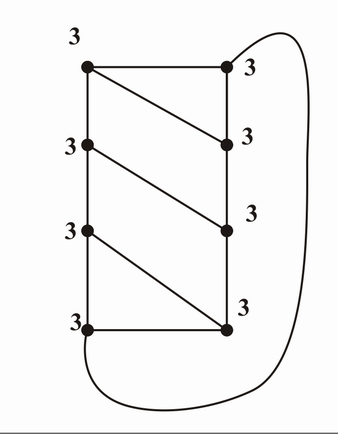
a) Beispielgraph G = 6[Bearbeiten | Quelltext bearbeiten]
Geben Sie ein Beispiel für einen kubischen Graphen mit an!
b) Kubischer Graph mit ungerader Knotenanzahl[Bearbeiten | Quelltext bearbeiten]
Gibt es einen kubischen Graphen mit ungerader Knotenanzahl ?
Somit können wir in den Aufgabenstellungen einen ungerichten Graphen ohne Mehrfachkanten nur dann zeichnen, wenn das Handschlaglemma gilt: Die Summe über die Grade aller Knoten eines Graphen ist gleich der doppelten Kantenanzahl in dem Graphen.
Da die doppelte Kantenanzahl gerade ist, muss die Summe über die Grade aller Knoten auch gerade sein. In der Summe darf ich beliebig Klammern setzen, also auch einmal um alle geraden Summanden (diese Summe ist auf jeden fall gerade), und dann einmal um alle ungeraden Summanden; damit die zweite Summe gerade ist, muss die anzahl deren Summanden gerade sein. Nun ist aber jeder Summand Grad eines Knotens; diese Knoten haben alle ungeraden Grad; d.h. die Anzahl der Knoten mit ungeradem Grad ist gerade.
Da aber die Anzahk der Knoten mit ungeradem Knotengrad ungerade ist, kann ein solcher kubischer Graph nicht existieren!
c) Verallgemeinerung kubischer Graph[Bearbeiten | Quelltext bearbeiten]
Zeigen Sie, daß es zu jedem einen kubischen Graphen mit gibt!
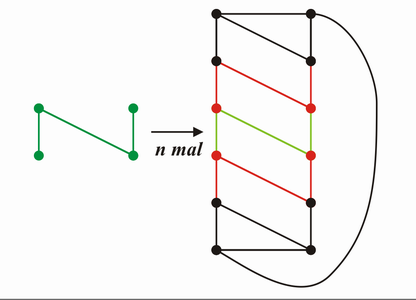
Der kubische Graph mit z.B. n = 8 schaut von der Anordnung so aus:
"unterer Teil" "oberer Teil"
|-----------------------------------|
3 2 1 1 2 3
| |-------------------+---|
|-----------------------|
^^^^^^^^^^^^^^^^^^^^
2 1 1 2
einfügen n mal