TU Wien:Mathematik 1 UE (diverse)/Übungen WS06/Beispiel 176

Angabe

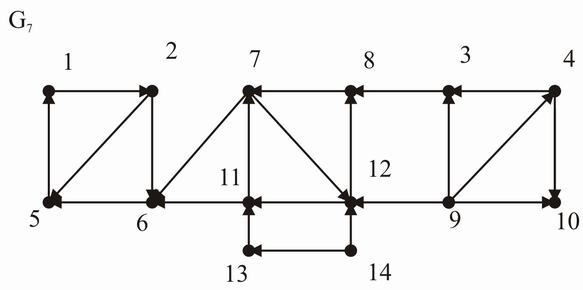
Man bestimme die starken Zusammenhangskomponenten und die Reduktion $G_{7R}$ des Graphen $G_{7}$.

Theoretische Grundlagen (von mnemetz)

Ein ungerichteter Graph G heißt zusammenhängend, wenn jeder Knoten y von jedem Knoten x aus erreichbar ist.

In einem gerichteten Graph fasst man jene Knoten zu einer starken Zusammenhangskomponente zusammen, die selbst von jedem dieser Knoten erreichbar sind. Sollte ein Knoten nur in einer Richtung erreichbar sein, so wird er selbst zu einer starken Zusammenhangskomponente.

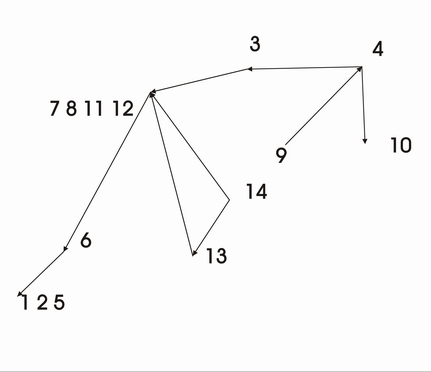
Bei der Reduktion eines Graphen werden die starken Zusammenhangskomponenten zu einem Punkt zusammengefasst und dann verbunden.

Lösungsvorschlag der Lerngruppe vom 26.12.2005

Starke Zusammenhangskomponenten

• 1-2-5
• 7-12-8-11
• Einzelne Punkte 6, 13, 14, 3, 9, 4, 10

Graphentheoretische Reduktion