TU Wien:Mathematik 1 UE (diverse)/Übungen WS06/Beispiel 195

Angabe

Man zeige, daß es in jedem einfachen Graphen G mit n $\geq$ 2 Knoten wenigstens zwei Knoten mit gleichem Knotengrad gibt.

Lösungsvorschlag von mnemetz

Aufzeichnen eines Graphen gegen die Annahme

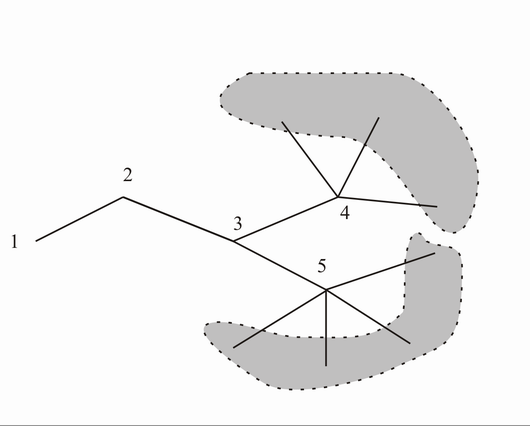
Zuerst zeichne ich mir einen Graphen, in dem keine gleichen Knotengrade vorkommen. Wie unschwer zu sehen ist, müsste dieser Graph immer weiter "knospen":

Erste Auffälligkeit: Widerspruch zur Formalisierung eines Graphen

Zuerst betrachte ich, wie ein Graph über Mengen formal dargestellt wird:

Ein einfacher Graph $G=\langle V,E\rangle$ ohne Schlaufen kann formalisiert werden als ein Paar aus einer endlichen Menge V (vertex, Knoten) und einer Menge E (edge, Kante) von Mengen von zwei Elementen aus V.

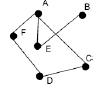
Beispiel:

G = ({A, B, C, D, E, F}, {{A, E}, {B, E}, {A, C}, {A, F}, {F, D}, {D, C}})

Damit wird schon klar, dass der Widerspruch sich aus der angegebenen Endlichkeit der Mengen ergeben muss.

Eine alternative Formalisierung eines Graphen wäre:

Ein einfacher Graph (ohne Schlaufen) ist ein Paar $G=\langle V,T\rangle$ aus einer endlichen Menge V und einer symmetrischen (und irreflexiven) Relation $T=V\times V$

G = ({A, B, C, D, E, F}, {(A, E), (B, E), (A, C), (A, F), (F, D), (D, C), (E, A), (E, B), (C, A), (F, A), (D, F), (C, D)})

Wiederum endlich ...

Ich verstehe diese Hinweise auf die Endlichkeit als eine Ergänzung zum o.g. unendlich knospenden Graphen, noch nicht als endgültige Bestätigung, dass es in einem schlichten, ungerichteten Graphen mindestens 2 Knoten gleichen Knotengrades gibt.

Betrachtungen eines schlichten Graphen

Ich taste mich mit einigen einleitenden Betrachtungen (erster Punkt ist FUNDAMENTAL WICHTIG!)

1. Ein Graph, der nur aus einem Punkt besteht: In diesem hat der einzige Knoten den Knotengrad 0. Diese Betrachtung können wir ausser Acht lassen, da bekanntlich gilt: Ein einfacher Graph $G=\langle V,E\rangle$ ohne Schlaufen kann formalisiert werden als ein Paar aus einer endlichen Menge V (vertex, Knoten) und einer Menge E (edge, Kante) von Mengen von zwei Elementen aus V. (man beachte die Hervorhebung!)
2. Erweitern wir den Graph um eine Kante, so haben beide Knoten den Knotengrad 1.
3. Hängen wir wieder eine Kante dran, so hat ein Knoten Knotengrad 2, die andern 1.
4. usw.

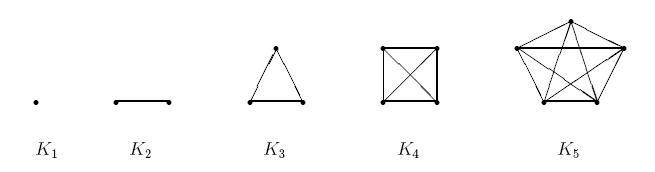
So betrachte ich nun vollständige Graphen. Ein Graph heisst vollständig, wenn jede Ecke mit jeder anderen Ecke durch genau eine Kante verbunden ist.

$K_{n}$ bezeichnet den vollständigen Graphen mit n Ecken.

Solche vollständige Graphen sind für uns deshalb interessant, weil sie einfache Graphen mit der maximal möglichen Kantenanzahl darstellen. Betrachten wir z.B. $K_{4}$. Jede Ecke hat Knotengrad n-1, wobei n die Anzahl der Ecken insgesamt ist.

Diese Betrachtung ist fundamental, denn sie eröffnet uns die Erkenntnis, dass die Knotengrade aus der Menge

1,2,3,4, ... , n-1 (n ist die Anzahl der Ecken)

entnommen werden müssen. (0 lassen wir ausser acht, s.o.)

Aber hallo! Es gibt n Ecken, aber nur n-1 Elemente in o.g. Menge. Das bedeutet aber bei n Ecken, dass zwei Ecken denselben Knotengrad haben müssen.

Nun, dann schauen wir mal, was passieren würde, wenn man nun aus der o.g. Menge immer nur eines auswählen wollte, aber keines doppelt. Man müsste auch die 0 auswählen, aber dann ergibt sich aus 0 und n - 1 ein Widerspruch.

Schlussfolgerung

Um einen Graphen zu erstellen, bei dem jeder Knoten einen anderen Knotengrad hat, werden demnach immer mehr Möglichkeiten benötigt um die Punkte zu verbinden als Punkte gibt, was in einem einfachen Graphen nicht möglich ist.

$\Rightarrow$ In einem einfachen Graphen mit $n\geq 2$ ist es unmöglich, dass alle Knotengrade unterschiedlich sind.

$\Rightarrow$ Es müssen mindestens 2 Knoten einen gleichen Knotengrad haben.

Webressourcen

Die Lösung für dieses Beispiel habe ich im Informatik-Forum im Mathe 2-Bereich gefunden und zwar im Thread zum dortigen Beispiel G5. Ich bin mir nicht sicher, aber es scheint, dass es dasselbe Beispiel ist. --RolandU

Weitere Links: f.thread:9132&highlight=549 f.thread:30116&page=2&highlight=549 -- hanzzz

Google Groups Eintrag