TU Wien:Mathematik 1 UE (diverse)/Übungen WS06/Beispiel 210

Aufgabe

Zum Abarbeiten der Knoten eines Binärbaumes verwendet man gerne rekursive Algorithmen, die in wohldefinierter Reihenfolge die folgenden Schritte ausführen:
(1) Bearbeite den aktuellen Knoten,
(2) Gehe zur Wurzel des linken Nachfolgebaums des aktuellen Knotens,
(3) Gehe zur Wurzel des rechten Nachfolgebaums des aktuellen Knotens.
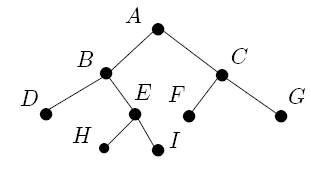
Am Beginn steht man bei der Wurzel des Gesamtbaumes. F?uhrt man die genannten Schritte (1) bis (3) rekursiv in der angegebenen Reihenfolge aus, so spricht man von Präordertraversierung. Beim untenstehenden Baum werden die Knoten also in folgender Reihenfolge bearbeitet: A;B;D;E;H; I;C; F;G. Wie ändert sich diese Reihenfolge, wenn man im Algorithmus jeweils die Abfolge (2)(1)(3) nimmt (Inordertraversierung), wie wenn man die Abfolge (2)(3)(1) wählt (Postordertraversierung)?

Lösungsvorschlag

Inordertraversierung

Abarbeitung:

1 Gehe zur Wurzel des linken Nachfolgebaums des aktuellen Knotens,
2 Bearbeite den aktuellen Knoten,
3 Gehe zur Wurzel des rechten Nachfolgebaums des aktuellen Knotens.

graphische Abarbeitung:


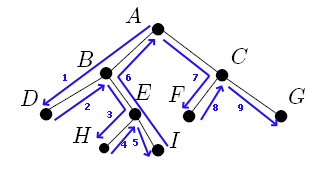
Reihenfolge:
D,B,H,E,I,A,F,C,G

Postordertraversierung

Abarbeitung:

1 Gehe zur Wurzel des linken Nachfolgebaums des aktuellen Knotens,
2 Gehe zur Wurzel des rechten Nachfolgebaums des aktuellen Knotens,
3 Bearbeite den aktuellen Knoten.

graphische Abarbeitung:


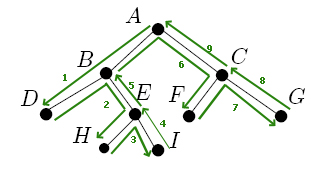
Reihenfolge:
D,H,I,E,B,F,G,C,A

Links

• f.thread:49303&highlight=Beispiel+210