TU Wien:Mathematik 1 UE (diverse)/Übungen WS06/Beispiel 567

Für die Vektoren ${\vec {x}}={\begin{pmatrix}1\\2\\3\end{pmatrix}}$, ${\vec {y}}={\begin{pmatrix}3\\-1\\2\end{pmatrix}}$ und ${\vec {z}}={\begin{pmatrix}2\\2\\1\end{pmatrix}}$ berechne man

(a) die Längen von ${\vec {x}}$,${\vec {y}}$ und ${\vec {z}}$

(b) den Winkel $\phi$ zwischen ${\vec {x}}$ und ${\vec {y}}$

(c) das Volumen des von ${\vec {x}}$,${\vec {y}}$ und ${\vec {z}}$ aufgespannten Parallelepipeds

Lösungsvorschlag von mnemetz

Längen der Vektoren

Die Länge eines Vektors wird bestimmt durch: $|{\vec {v}}|={\sqrt {a_{1}+a_{2}+\dots +a_{n}}}$.

• $|{\vec {x}}|={\sqrt {1^{2}+2^{2}+3^{2}}}={\sqrt {1+4+9}}={\sqrt {\mathit {14}}}$
• $|{\vec {y}}|={\sqrt {3^{2}+1^{2}+2^{2}}}={\sqrt {9+1+4}}={\sqrt {\mathit {14}}}$
• $|{\vec {z}}|={\sqrt {2^{2}+2^{2}+1^{2}}}={\sqrt {4+4+1}}={\sqrt {9}}={\mathit {3}}$

Winkel zwischen den Vektoren

Der Winkel zwischen den Vektoren ergibt sich aus der Formel (Cosinussatz):

• ${|{\vec {x}}-{\vec {y}}|}^{2}={|{\vec {x}}|}^{2}+{|{\vec {y}}|}^{2}-2*|{\vec {x}}|*|{\vec {y}}|*\cos \phi \qquad \Rightarrow \qquad \cos \phi ={\frac {{\vec {x}}*{\vec {y}}}{|{\vec {x}}|*|{\vec {y}}|}}$

Somit ergibt sich:

$\cos \phi ={\frac {{\begin{pmatrix}1\\2\\3\end{pmatrix}}*{\begin{pmatrix}3\\-1\\2\end{pmatrix}}}{{\sqrt {14}}*{\sqrt {14}}}}={\frac {3-2+6}{14}}={\frac {7}{14}}={\frac {1}{2}}$

$\phi ={\frac {\pi }{3}}=60^{\circ }$

Zur Erinnerung - die Umrechnungsformelm: Zuerst Angabe in Grad, danach in Bogenmaß. Die Umrechnungsformeln sind:

• Von Grad nach Bogenmaß:

${\rm {Winkel}}_{\rm {Bogenmass}}={\frac {{\rm {Winkel}}_{\rm {Grad}}\cdot \pi }{180}}$

• Von Bogenmaß nach Grad:

${\rm {Winkel}}_{\rm {Grad}}={\frac {{\rm {Winkel}}_{\rm {Bogenmass}}\cdot 180}{\pi }}$

Volumen des Parallelepipeds

Schematisch die Problemstellung:

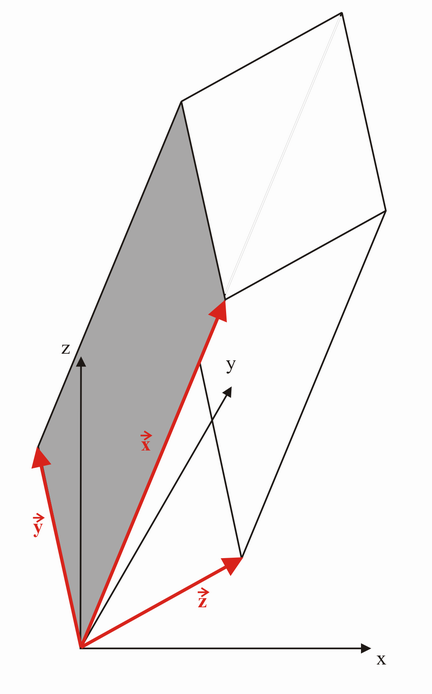
Das Volumen errechnet sich aus dem äusseren Produkt (Spatprodukt) der Vektoren ${\vec {x}}$ und ${\vec {y}}$, was wiederum einen Vektor ergibt. Dieser Vektor wird mit ${\vec {z}}$ multipliziert - das sich ergebende Skalar ist das Volumen.

Zur Erinnerung: Das Spatprodukt errechnet sich wie folgt:

(Anm: Eigentlich ist das Spatprodukt von ${\mathfrak {x}},{\mathfrak {y}},{\mathfrak {z}}$ so definiert (der Rechenweg bleibt aber richtig): $\det({\mathfrak {x}},{\mathfrak {y}},{\mathfrak {z}})$ oder eben $\langle {\mathfrak {x}}\times {\mathfrak {y}},{\mathfrak {z}}\rangle$. )

${\vec {x}}={\begin{pmatrix}x_{1}\\x_{2}\\x_{3}\end{pmatrix}},{\vec {y}}={\begin{pmatrix}y_{1}\\y_{2}\\y_{3}\end{pmatrix}}\Rightarrow {\vec {x}}\times {\vec {y}}={\begin{pmatrix}{\begin{vmatrix}x_{2}&y_{2}\\x_{3}&y_{3}\end{vmatrix}}\\-{\begin{vmatrix}x_{1}&y_{1}\\x_{3}&y_{3}\end{vmatrix}}\\{\begin{vmatrix}x_{1}&y_{1}\\x_{2}&y_{2}\end{vmatrix}}\end{pmatrix}}$

Somit müssen wir berechnen:

$({\begin{pmatrix}1\\2\\3\end{pmatrix}}\times {\begin{pmatrix}3\\-1\\2\end{pmatrix}})*{\begin{pmatrix}2\\2\\1\end{pmatrix}}={\begin{pmatrix}{\begin{vmatrix}2&-1\\3&2\end{vmatrix}}\\-{\begin{vmatrix}1&3\\3&2\end{vmatrix}}\\{\begin{vmatrix}1&3\\2&-1\end{vmatrix}}\end{pmatrix}}*{\begin{pmatrix}2\\2\\1\end{pmatrix}}={\begin{pmatrix}4+3\\-(2-9)\\-1-6\end{pmatrix}}*{\begin{pmatrix}2\\2\\1\end{pmatrix}}={\begin{pmatrix}7\\7\\-7\end{pmatrix}}*{\begin{pmatrix}2\\2\\1\end{pmatrix}}=14+14-7={\mathit {21}}$