TU Wien:Mathematik 1 UE (diverse)/Übungen WS06/Beispiel 86

Stellen Sie die folgenden Relationen im cartesischen Koordinatensystem und auch als gerichteten Graphen dar und untersuchen Sie weiters, ob eine Äquivalenzrelation vorliegt.

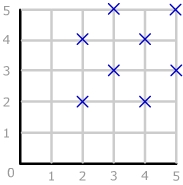
mRn <=> m + n gerade, m, n € {2,3,4,5}

Darstellung im cartesischen Koordinatensystem:

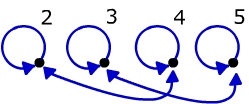
Darstellung anhand von gerichteten Graphen:

(R) - Reflexiv: Ja, da wie am Graphen schön ersichtlich aRa (sprich: jedes a steht in Relation zu a) (S) - Symmetrisch: Ja, da wie ebenfalls am Graphen schön ersichtlich aRb => bRa gilt! (T) - Transitiv: Ja, da aRb und bRc => aRc (die angegebene Menge {2,3,4,5} geht zwar nur bis 5, daher kann man eine Verdeutlichung durch ein Beispiel wie 2R4 u. 4R6 => 2R6 hier nicht bilden. Allerdings geht es ja darum zu bestimmen ob die Relation (T) ist oder nicht!)