TU Wien:Mathematik 1 UE (diverse)/Übungen WS06/Beispiel 91

Untersuchen Sie, ob die Relation $ARB\iff A△B=A$ ($△$ die symmetrische Differenz) auf der Potenzmenge einer Menge M eine Äquivalenzrelation bildet.

Siehe auch f.thread:23103 , f.thread:22874

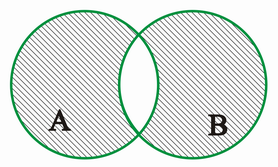
Definition der symmetrischen Differenz

$A△B=(A\setminus B)\cup (B\setminus A)$

C heißt symmetrische Differenz der Mengen A und B,

$C=A\mathrm{△}B$,

wenn C alle Elemente aus A enthält, die nicht zu B gehören und alle Elemente aus B, die nicht zu A gehören, d.h.:

$A\mathrm{△}B=(A-B)\cup (B-A)$

VENN-Diagramm:

Reflexivität

Reflexivität heißt, dass jedes Element in Relation zu sich selbst steht:

die Relation ist definiert : A $△$ B = A

dh: wenn A in relation mit A steht => A $△$ A = A

Aber das ergibt nicht A, sondern eine leere Menge => nicht reflexiv

Symmetrie

$ARB\Rightarrow BRA$?

Symmetrie heißt, wenn für alle a,b mit aRb auch bRa folgt.

$\mathrm{\forall }\text{ a,b }\in A^2:\text{ (a,b) }\in \text{ R }\Rightarrow \text{ (b,a) }\in \text{ R }$

Aus der Definition der symmetrischen Differenz folgt:

$\begin{array}{ccc}A△B=A& \iff & A=\mathrm{\varnothing }\\ B△A=B& \iff & B=\mathrm{\varnothing }\end{array}$

Daher ist die Relation R nur dann symmetrisch, wenn A = B. D. h. sie ist im allgemeinen nicht symmetrisch.

Transitivität

$ARB\wedge BRC\Rightarrow ARC$?

Eine Relation R transitiv, wenn stets gilt: (a,b) aus R UND (b,c) aus R FOLGT (a,c) aus R

$\mathrm{\forall }\text{ a,b }\in \text{ R }:\text{ (a,b) }\in \text{ R }\wedge \text{ (b,c) }\in \text{ R }\Rightarrow \text{ (a,c) }\in \text{ R }$

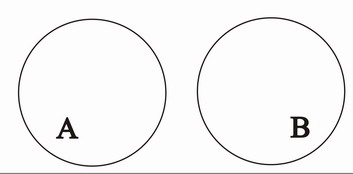
Zwei Mengen A und B können entweder disjunkt sein ...

---

Die Mengen A und B heißen disjunkt, wenn gilt:

$A\cap B=\varnothing$

$\varnothing$ symbolisiert eine leere Menge.

Als VENN-Diagramm dargestellt:

---

... oder sich schneiden. Anhand der oben angeführten Definition der symmetrischen Differenz sieht man leicht, daß $A△B$ die Menge $A\cup B$ ist, wenn die Mengen disjunkt sind, oder aber die Vereinigung zweier echter Teilmengen von jeweils A und B umfaßt, wenn sie nicht disjunkt sind. Daher kann $A△B=A$ nur gelten, wenn $B=\mathrm{\varnothing }$ und damit $A△B=A△\mathrm{\varnothing }=(A\setminus \mathrm{\varnothing })\cup (\mathrm{\varnothing }\setminus A)=A$ gilt.

Daraus kann man folgern:

$\begin{array}{ccc}A△B=A& ⟺& B=\mathrm{\varnothing }\\ B△C=B& ⟺& C=\mathrm{\varnothing }\end{array}$

Und damit gilt:

$A△C=A△\mathrm{\varnothing }=A$

Daraus folgt, daß die Relation R transitiv ist.