TU Wien:Mathematik 1 UE (diverse)/Übungen WS07/Beispiel 191
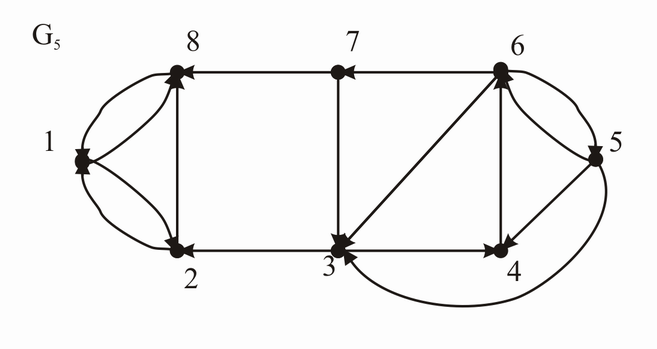
Man bestimme die Adjazenzmatrix sowie (mit deren Hilfe) die Anzahl der gerichteten Kantenfolgen der Länge 3 von 4 nach 6!
Nützliches[Bearbeiten | Quelltext bearbeiten]
Adjazenzmatrix
Wikipedia Erreichbarkeitsmatrix
Multiplizieren von Matrizen
Lösungsvorschlag von W wallner[Bearbeiten | Quelltext bearbeiten]
Adjazenzmatrix des Graphen
Adjazenzmatrix multipliziert mit sich selbst:
Adjazenzmatrix hoch 3:
Man sieht in der 4. Zeile, 6. Spalte, dass es genau einen Weg der Länge 3 vom Punkt 4 zum Punkt 6 gibt ( 4 -> 6 -> 5 -> 6 ).
Frage von CG: Sicher dass die Potenzmatrizen und so stimmen? Ich sitze schon seit einer Ewigkeit und suche nach moeglichen Fehlern in meiner Version aber ich komme einfach nicht auf das selbe Ergebnis. Danke
Kann bestätigen das mit den Matrizen etwas nicht stimmen kann. Beim ersten hinschauen müsste bei für das Feld (1,1) der Matrize ja schon 2 rauskommen.
Lösungsvorschlag von der Lerngruppe vom 26.12.2005[Bearbeiten | Quelltext bearbeiten]
(Dank an Sarah!)
Anzahl der gerichteten Kantenfolgen mit Länge 3 von 4 nach 6: 2
Anmerkung: Da es ein gerichteter Graph ist (man beachte die Pfeilrichtungen!), gibt es keine Verbindung von 4 nach 3!