TU Wien:Algebra und Diskrete Mathematik VU (diverse)/Übungen 2025W/Beispiel 328
Zur Navigation springen
Zur Suche springen
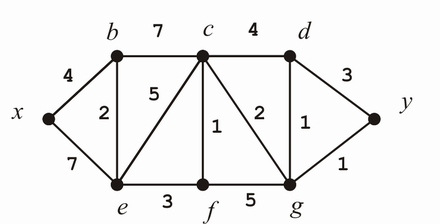
Bestimmen Sie mit dem Algorithmus von Dijkstra einen kürzesten Weg zwischen den Knoten x und y im folgenden Graphen:
Dieses Beispiel hat einen unbekannten Lösungsstatus. Bitte editiere diese Seite und schreibe den dir bekannten Status ins Beispiel. Die möglichen Werte sind hier: Vorlage:Beispiel dokumentiert. Führe folgende Änderung durch:
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
Theorie - Algorithmus von Dijkstra[Bearbeiten | Quelltext bearbeiten]
- Siehe TU_Wien:Mathematik_1_UE_(diverse)/Theorie_WS05/06.12.2005_Graphentheorie#K.C3.BCrzeste_Wege_.28Dijkstra-Algorithmus.29!
- Eine Erklärung des Algorithmus unter Verwendung einer Tabelle gibt es im Video Der Dijkstra-Algorithmus auf YouTube.
Lösungsvorschlag von mnemetz[Bearbeiten | Quelltext bearbeiten]
Tabellarische Lösung[Bearbeiten | Quelltext bearbeiten]
| Iteration | x | b | c | d | e | f | g | y | Auswahl | Vorgänger |
| 0 | 0 | x | ||||||||
| 1 | 4 | 7 | b | x | ||||||
| 2 | 11 | 6 | e | b | ||||||
| 3 | 11 | Fehler beim Parsen (⧼math_empty_tex⧽): {\displaystyle } | 9 | f | e | |||||
| 4 | 10 | 14 | c | f | ||||||
| 5 | 14 | 12 | g | c | ||||||
| 6 | 13 | 13 | y |
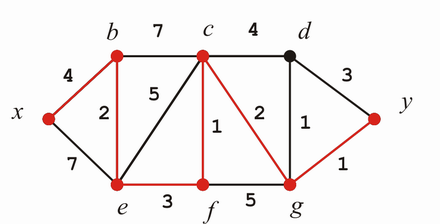
Kürzester Weg somit: