TU Wien:Algebra und Diskrete Mathematik VU (diverse)/Übungen 2025W/Beispiel 349
Untersuchen Sie, ob die Menge M mit der Operation ein Gruppoid, eine Halbgruppe, ein Monoid bzw. eine Gruppe ist.
, d.h. die Potenzmenge der Menge A,
{{Beispiel|1=
Angabetext
}}
oder
{{Beispiel|
Angabetext
}}
zu (im Falle einer korrekten, unverifizierten Lösung "solved". Auch möglich "unsolved", "wrong", "verified_by_tutor". Alle möglichen Werte sind hier: Vorlage:Beispiel dokumentiert.)
{{Beispiel|status=solved|1=
Angabetext
}}
Hilfreiches[Bearbeiten | Quelltext bearbeiten]
Gruppeneigenschaften[Bearbeiten | Quelltext bearbeiten]
Gesetze und Eigenschaften von algebraischen Strukturen
Eine algebraische Struktur ist eine nichtleere Menge G mit einer oder mehreren Operationen.
Folgende Eigenschaften kann eine solche Struktur annehmen:
- Abgeschlossenheit: für ist (d.h. ist eindeutig zugeordnet). Das entspricht einer Funktion
- Assoziativgesetz: für alle .
- Einheitselement (bzw. Neutrales Element): Es existiert ein , so dass für alle gilt: .
- Inverses Element: Für jedes gibt es ein inverses Element (oder auch ) so, dass gilt . Wobei das e das Einheitselement ist.
- Kommutativgesetz: für alle .
| Nr. | Gruppoid | Halbgruppe | Monoid | Gruppe | Abelsche Gruppe |
|---|---|---|---|---|---|
| 1 | ✓ | ✓ | ✓ | ✓ | ✓ |
| 2 | ✓ | ✓ | ✓ | ✓ | |
| 3 | ✓ | ✓ | ✓ | ||
| 4 | ✓ | ✓ | |||
| 5 | ✓ |
Lösungsvorschlag von mnemetz[Bearbeiten | Quelltext bearbeiten]
Basierend auf f.thread:37701
Abgeschlossenheit: Wenn gilt, dass , folgt daraus, dass auch . Abgeschlossenheit ist gegeben.
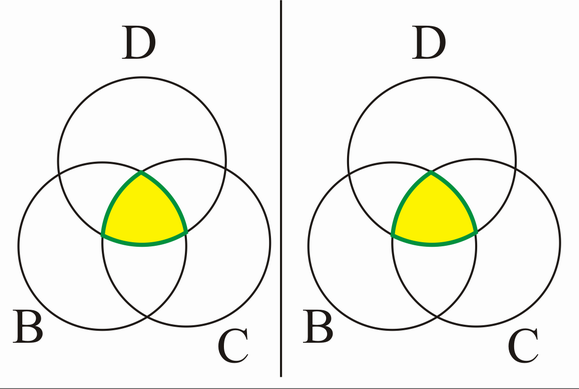
Assoziativität: Es muss gelten: für alle . Dies ist wahr, wie die folgenden Venn-Diagramme für beide Sachverhalte (rechts bzw. links) zeigen!
Das neutrale Element ist nicht die leere Menge, sondern A.Egal, welche Menge B man mit A schneidet, es kommt wieder die Menge B heraus. Das einzige Element, das invertierbar ist, ist wiederum A, (neutrales Element ist immer invertierbar), denn für jede echte Teilmenge B von A existiert keine Menge C, so daß B geschnitten C gleich A ist.
Die Operation ist kommutativ.
Folgerung: Für A = {} handelt es sich um eine kommutative Gruppe, für um ein kommutatives Monoid.
Siehe auch: f.thread:37912