TU Wien:Mathematik 1 UE (diverse)/Übungen WS10/Beispiel 32

Man finde alle sechsten Wurzeln von z = −27 in $ℂ$ und stelle sie in der Gaußschen Zahlenebene dar.

Lösungsvorschlag

Zuerst die Zahl in Polarkoordinaten darstellen:

Das ist in dem Fall relativ einfach: Der Betrag ist 27 und der Winkel ist -180° bzw. $-\pi$

---

Anmerkung

Natürlich ist es genau so gut wenn man den Winkel mit +180° also $\pi$ annimmt. Weiß nicht mehr, warum ich damals ausgerechnet mit Minus gerechnet habe, aber es muss natürlich das Gleiche herauskommen

--MatheFreak 22:26, 30. Mär. 2011 (CEST)

---

$-27=[27,-\pi ]$

genauer gesagt it es:

$-27=[27,-\pi +2\cdot n\cdot \pi ]=[27,\pi \cdot (2\cdot n-1)]n\in \mathbb{N}$

weil sich der Winkel alle $2\cdot \pi$ wiederholt

Und lt. der Rechenregeln kann man nun die Wurzel ziehen, in dem man vom Betrag die Wurzel zieht und den Winkel durch die Wurzel dividiert:

$a=\sqrt[6]{-27}=[\sqrt[6]{27},\frac{\pi }{6}\cdot (2\cdot n-1)]$

daraus ergeben sich nun die folgenden Lösungen:

der Maßstab stimmt nicht, aber von den Winkeln her ist es korrekt; durch die Lösungen ergibt sich ein regelmäßiges Sechseck

$n=1:a_1=[\sqrt[6]{27},\frac{\pi }{6}]$
$n=2:a_2=[\sqrt[6]{27},\frac{\pi }{2}]$
$n=3:a_3=[\sqrt[6]{27},\frac{5\cdot \pi }{6}]$
$n=4:a_4=[\sqrt[6]{27},\frac{7\cdot \pi }{6}]$
$n=5:a_5=[\sqrt[6]{27},\frac{3\cdot \pi }{2}]$
$n=6:a_6=[\sqrt[6]{27},\frac{11\cdot \pi }{6}]$
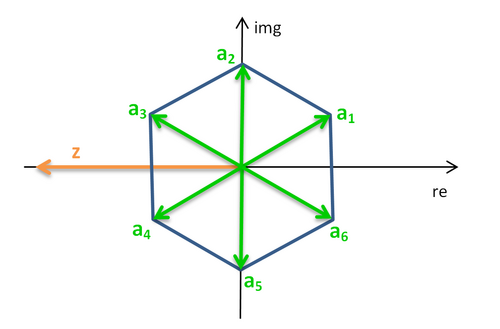
und ab hier wiederholt es sich:
$n=7:a_7=[\sqrt[6]{27},\frac{13\cdot \pi }{6}]=[\sqrt[6]{27},\frac{\pi }{6}]=a_1$

Fehler?

Ist Phi nicht -90° bzw. 3*Pi/2 ? Weil z=-27 => z=0-27i, also -27 senkrecht und nicht waagrecht im Koordinatensystem.

Die Argumentation versteh ich nicht. Wie kommst du auf z=-27 => z=0-27i ??

$-27=-27+0\cdot i=27\cdot \cos 180+27\cdot \sin 180\cdot i$

oder in Worten: -27 ist zwar negativ aber auf jeden Fall rein reel. Bei einem Winkel von 90° wäre der Wert rein imaginär

--MatheFreak 22:18, 30. Mär. 2011 (CEST)