TU Wien:Mathematik 1 UE (diverse)/Theorie WS05/22.11.2005
Intention[Bearbeiten | Quelltext bearbeiten]
Diese Präsentationsgrundlage ist nicht darauf ausgerichtet, die Gebiete
- Mengen
- Relationen
- Funktionen von Mengen
zu erläutern, sondern wurde konzipiert als Grundgerüst für die theoretische Grundlage der Beispiele, die am 23.11.2005 in den Übungsgruppen vorbereitet sein müssen. --Mnemetz 17. Nov 2005 11:03 (CET)
Mengen[Bearbeiten | Quelltext bearbeiten]
Alle Bezeichnungen der Mengenlehre tauchen in der einen oder anderen Form als Hilfsmittel in allen Teilbereichen der Mathematik auf, da sie eine kurze und übersichtliche Darstellung von Sachverhalten ermöglichen.
Definition von Mengen[Bearbeiten | Quelltext bearbeiten]
Ein Kleinkind bekommt eine Schachtel voller Duplo-Steine in verschiedenen Farben. Das Kind sortiert nun alle roten Steine aus und bildet damit die "Menge der roten Steine".
Was lernen wir daraus Allgemeines bezüglich Mengenbildung? Bei dieser werden Objekte
- ausgesondert
- und zusammengefasst.
Naive Mengenlehre[Bearbeiten | Quelltext bearbeiten]
Georg CANTOR (1845-1918) definiert "Menge" folgendermaßen:
Definition: Unter einer Menge ist die Zusammenfassung von bestimmten, wohlunterscheidbaren Objekten zu einem Ganzen zu verstehen. Die Objekte, die zu einer Menge zusammengefasst werden, heißen Elemente dieser Menge.
Die Elemente müssen also einem Auswahlkriterium standhalten. Ebenso muss das Auswahlkriterium entsprechend gewählt werden.
Mit der Wohlunterscheidbarkeit geht die Forderung einher, dass die Elemente der Menge klar trennbar sein müssen! Beispiel: Menge aller Buchstaben von "glatt" entspricht "M = {g,l,a,t} ".
Ob ein Element zu einer Menge gehört beschreibt man kurz als ; gehört es nicht dazu, dann als
Russels' Paradoxon[Bearbeiten | Quelltext bearbeiten]
Die Formulierungen der naiven Mengenlehre führen jedoch in gewissen Fällen zu Paradoxien!
Die Russellsche Antinomie ist ein von Bertrand Russell formuliertes Paradoxon auf der Grundlage der naiven Mengenlehre. Die Menge M ist definiert als die "Menge aller Mengen, die sich nicht selbst enthalten".
Diese Definition führt zu einem Widerspruch, da sich demzufolge M sowohl selbst enthält als auch nicht selbst enthält.
Es gibt zahlreiche populäre Formulierungen der Russellschen Antinomie. Bekannt ist der Barbier, der alle Männer im Ort rasiert, die sich nicht selbst rasieren. Die Frage, ob sich der Barbier selbst rasiert oder nicht, führt ebenfalls zu einem Widerspruch (Barbier-Paradoxon).
Durch den axiomatischen Aufbau der Mengenlehre lassen sich Antinomien vermeiden. Er zeigt, dass die Zusammenfassung aller Mengen, die sich nicht selbst enthalten, keine Menge sein kann, sondern eine Klasse bildet - eben weil das sonst zu einem Widerspruch führt. Die Klassendefinition dieser Mengenzusammenfassung ist jedoch in sich widerspruchsfrei und bildet die leere Klasse.
Mengenangaben[Bearbeiten | Quelltext bearbeiten]
Beschreibende Mengenangabe[Bearbeiten | Quelltext bearbeiten]
Auch deskriptive Mengenangabe genannt.
Die Menge A besteht also aus allen Elementen x, die die Eigenschaften P besitzen.
Statt dem | wird manchmal auch : geschrieben.
Aufzählende Mengenangabe[Bearbeiten | Quelltext bearbeiten]
Auch enumerative Mengenangabe genannt: Dabei werden die Elemente der Menge explizit angegeben:
Z.B. alle Elemente eines Würfels.
Veranschaulichung durch Venn-Diagramme[Bearbeiten | Quelltext bearbeiten]
Mengen werden sehr oft durch VENN-Diagramme veranschaulicht.
Der von dr Kurve umschlossene Bereich smybolisiert die Elemente der Menge A.
Spezielle Relationen zwischen Mengen[Bearbeiten | Quelltext bearbeiten]
Betrachten wir nun einige spezielle Beziehungen zwischen zwei Mengen A und B und einige Operationen, bei denen den Mengen A und B eine Menge C zugeorndet wird.
Teilmenge[Bearbeiten | Quelltext bearbeiten]
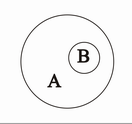
Die Menge B heißt Teilmenge von A
wenn jedes Element von B auch in A ist, d.h.
Als Venn-Diagramm dargestellt:
Gleichheit[Bearbeiten | Quelltext bearbeiten]
Die Mengen A und B heißen gleich (A = B), wenn jedes Element von A auch in B ist und umgekehrt. D.h. A ist eine Teilmenge von B und B eine Teilmenge von A:
echte Teilmenge[Bearbeiten | Quelltext bearbeiten]
Eine echte Teilmenge ist die Menge B dann von A (), wenn B eine Teilmenge von A ist aber B ungleich A is. d.h.:
Manchmal wird auch das Symbol verwendet.
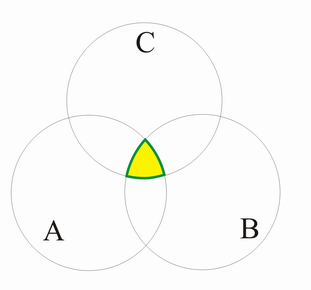
Durchschnitt[Bearbeiten | Quelltext bearbeiten]
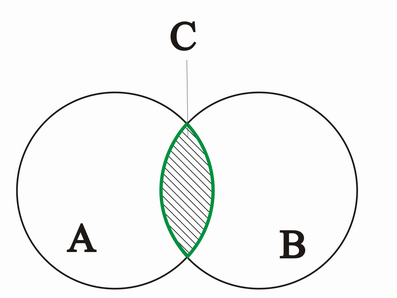
Die Menge C heißt Durchschnitt der Mengen A und B (sprich folgende symbolische Darstellung als "C ist A geschnitten B"),
wenn C die Menge aller Elemente ist, die sowohl in a als auch in B liegen, d.h.:
Als VENN-Diagramm dargestellt:
Die Definition des Durchschnittes auf ein beliebiges System von Mengen erweitert bedeutet:
(Der Durchschnitt dieser Mengen ist die Menge aller Elemente ...)
Disjunktivität[Bearbeiten | Quelltext bearbeiten]
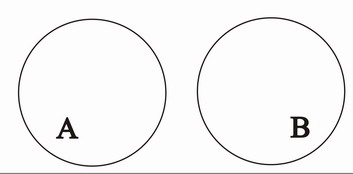
Die Mengen A und B heißen disjunkt, wenn gilt:
symbolisiert eine leere Menge.
Als VENN-Diagramm dargestellt:
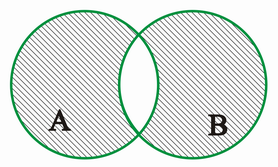
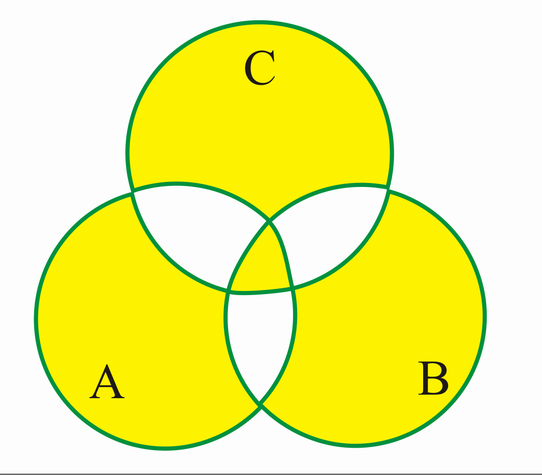
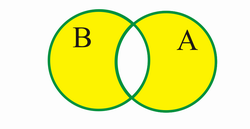
Vereinigung[Bearbeiten | Quelltext bearbeiten]
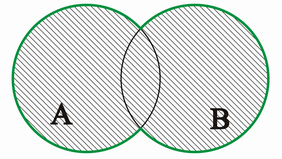
C ist dann die Vereinigungsmenge vn A und B
wenn C die Menge aller Elemente ist, die in A oder in B oder in beiden Mengen liegen, d.h.:
steht für "oder".
VENN-Diagramm:
Die Definition der Vereinigung auf ein beliebiges System von Mengen erweitert bedeutet:
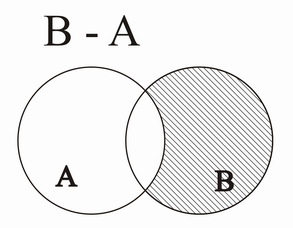
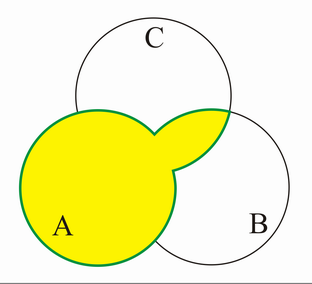
Differenz[Bearbeiten | Quelltext bearbeiten]
Die Differenzmenge C = A - B (manchmal auch c = A\B besteht aus den Elementen von A, die nicht in B liegen, d.h.:
C = B - A als VENN-Diagramm:
Wenn , so gilt: .
"Universum"[Bearbeiten | Quelltext bearbeiten]
Der Begriff Universum steht in der (diskreten) Mathematik für das so genannte Mengenuniversum U. Es fasst beliebige bekannte und unbekannte, über Axiome definierte Objekte zusammen, auch Mengen von Objekten.
Symmetrische Differenz[Bearbeiten | Quelltext bearbeiten]
C heißt symmetrische Differenz der Mengen A und B,
,
wenn C alle Elemente aus A enthält, die nicht zu B gehören und alle Elemente aus B, die nicht zu A gehören, d.h.:
VENN-Diagramm:
Cartesisches Produkt[Bearbeiten | Quelltext bearbeiten]
C ist ein cartesisches Produkt der Mengen A und B,
,
wenn C die Menge aller geordneten Paare von den Elementen und ist, d.h.:
.
symbolisieren geordnete Paare, n-Tupel, etc.
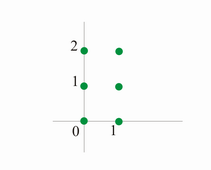
Cartesische Koordinaten[Bearbeiten | Quelltext bearbeiten]
Beispiel:
A = {0,1}, B = {0,1,2}
Darstellung der Elemente als "Koordinatensystem:
Operationen zwischen Mengen[Bearbeiten | Quelltext bearbeiten]
Kommutativgesetze[Bearbeiten | Quelltext bearbeiten]
Vertauschungsgesetze - möglich ist:
Assoziativgesetze[Bearbeiten | Quelltext bearbeiten]
Verknüpfungsgesetze, möglich sind:
Distributivgesetze[Bearbeiten | Quelltext bearbeiten]
Auch Verteilungsgesetze genannt.
Allgemeiner mit Mengen:
De Morgan'sche Gesetze[Bearbeiten | Quelltext bearbeiten]
Diese Gesetze behandeln die Relationen zwischen Komplement-Mengen (d.h. "umgekehrten" Mengen").
Potenzmenge[Bearbeiten | Quelltext bearbeiten]
Die Potenzmenge der Menge A (), ist die Menge, deren Elemente alle Teilmengen der Menge A sind, d.h.:
Relationen[Bearbeiten | Quelltext bearbeiten]
Definition[Bearbeiten | Quelltext bearbeiten]
Eine allgtemeine Beschreibung der Beziehung für Teilmengen U,V einer vorgegebenen Menge M. d.h.
kann z.B. so vorgenommen werden, daß die Teilmenge
des cartesischen Produktes vorgegeben wird.
U und V stehen genau dann in der Relation "", wenn das geordnete Paar in R liegt.
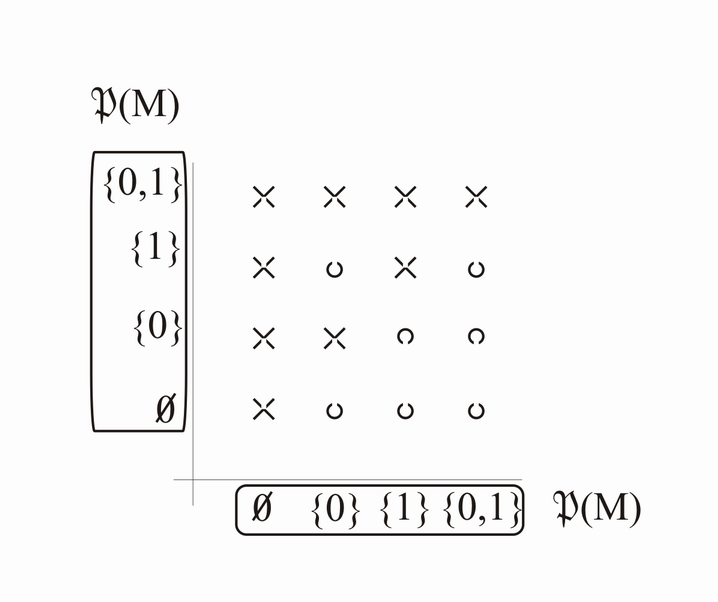
Betrachten wir die Menge M={0,1}, d.h.:
- in der folgenden Grafix die mit x markiertten Punkte:
Eine allgemeine Definition: Die zweistellige Relation R auf einer Menge A ist eine Teilmenge des cartesischen Produktes . Sind a,b A, so steht A in Relation zu B genau dann, wenn gilt. Die übliche Schreibweise ist aRb.
Gerichtete Graphen[Bearbeiten | Quelltext bearbeiten]
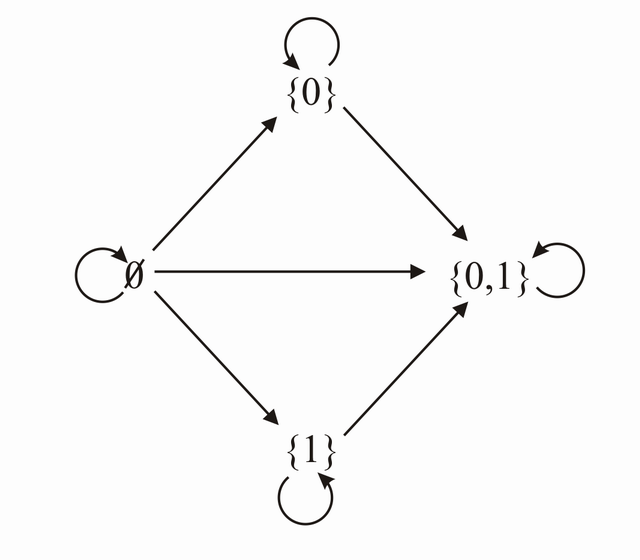
Relationen können als gerichtete Graphen symbolisch dargestellt werden. Dieser besteht aus einer Menge von "Knoten", und zwar den Elementen der Menge A, sowie einer Menge von gerichteten Kanten (durch Pfeile dargestellt), die von einem "Knoten" U genau dann zu einem Knoten V führen, wenn das geodnete Paar in R liegt.
Beispiel eines gerichteten Graphen der Relation "" auf A = ({0,1}):
Äquivalenzrelation[Bearbeiten | Quelltext bearbeiten]
Bei einer Äquivalenzrelation müssen Reflexivität, Symmetrie und Transitivität gemeinsam vorliegen.
Reflexivität[Bearbeiten | Quelltext bearbeiten]
Reflexivität heißt, dass jedes Element in Relation zu sich selbst steht:
Symmetrie[Bearbeiten | Quelltext bearbeiten]
Symmetrie heißt, wenn für alle a,b mit aRb auch bRa folgt.
Transitivität[Bearbeiten | Quelltext bearbeiten]
Eine Relation R transitiv, wenn stets gilt: (a,b) aus R UND (b,c) aus R FOLGT (a,c) aus R
Klasseneinteilung[Bearbeiten | Quelltext bearbeiten]
Eine Zerlegung einer Menge A in leere, paarweise disjunkte Teilmengen heißt Klasseneinteilung oder Partitionierung der Menge.
In der Mengenlehre heißen zwei Mengen A und B disjunkt oder elementfremd, falls sie kein gemeinsames Element besitzen.
Gleichbedeutend dazu ist folgende formale Definition:
Zwei Mengen A und B heißen disjunkt, wenn A geschnitten mit B leer ist:
Mehrere Mengen heißen paarweise disjunkt, wenn je zwei von ihnen disjunkt sind.
Eine disjunkte Mengenfamilie
ist eine Familie von paarweise disjunkten Mengen. Es gilt also
- für .
Die Vereinigung M eines disjunkten Mengensystems bezeichnet man als disjunkte Vereinigung und schreibt sie als
Ein Mengensystem U von Teilmengen einer Menge X heißt Partition von X, wenn gilt:
- die Vereinigung aller Mengen in U ist wieder ganz X,
- U ist eine disjunkte Mengenfamilie,
- die leere Menge ist nicht Element von U.
Vgl. auch Einteilung in Restklassen bei modulo-Beispielen.
Halbordnungsrelation[Bearbeiten | Quelltext bearbeiten]
Eine Relation R auf die Menge A heißt Halbordnungsrelation, wenn folgende Bedingungen erfüllt sind:
Reflexivität[Bearbeiten | Quelltext bearbeiten]
Reflexivität heißt, dass jedes Element in Relation zu sich selbst steht:
Identität[Bearbeiten | Quelltext bearbeiten]
Transitivität[Bearbeiten | Quelltext bearbeiten]
Eine Relation R transitiv, wenn stets gilt: (a,b) aus R UND (b,c) aus R FOLGT (a,c) aus R
Hasse-Diaramm[Bearbeiten | Quelltext bearbeiten]
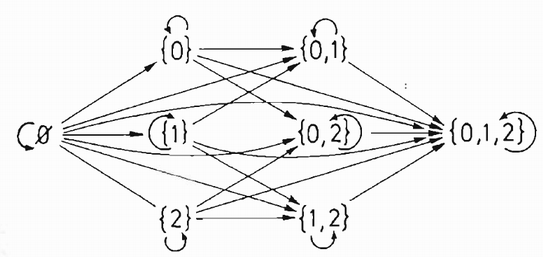
Betrachten wir die Halbordnung "" auf - als gerichteten Graphen ergibt sich:
Die Darstellung kann man vereinfachen, wenn man die vorliegende Halbordnung berücksichtigt:
- Wegen der Refexivität kann man alle Schlingen weglassen.
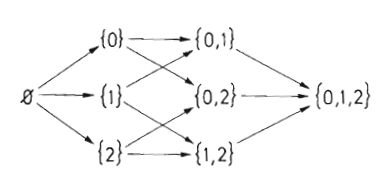
- Wegen der Transitivität genügt es, nur die gerichteten Kanten zum "direkten" Nachfolger zu zeichnen.
Ergibt folgende Vereinfachung:
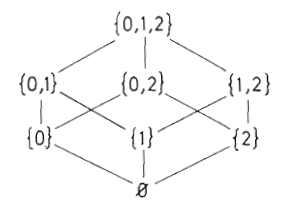
Wenn man nun vereinbart, dass die Kanten stets als nach oben gerichtet zu betrachten sind, ergibt sih als weietre Vereinfachung:
Dies ist dann das Hasse-Diagramm.
Funktionen, Kardinalzahl von Mengen[Bearbeiten | Quelltext bearbeiten]
Funktion (Abbildung)[Bearbeiten | Quelltext bearbeiten]
Definition der Funktion[Bearbeiten | Quelltext bearbeiten]
A und B seien zwei nichtleere Mengen. Unter einer Funktion (oder Abbildung) f von A in B versteht man dann eine Vorschrift, die jedem ein eindeutig bestimmbares zuordnet,
b wird dann das Bild von a unter f genannt, b = f(a).
A ist dann der Definitionsbereich, B der Wertevorrat von f.
Injektivität[Bearbeiten | Quelltext bearbeiten]
Eine Funktion ist dann injektiv, wenn jedes Element höchstens einmal als Bild des Elementes auftritt, d.h.:
oder
.
Man sagt auch eineindeutige Abbildung von A in B oder 1-1 Abbildung von A in B).
Surjektivität[Bearbeiten | Quelltext bearbeiten]
Eine Funktion ist dann surjektiv, wenn jedes mindestens einmal als Bild eines Elementes unter f auftritt, d.h.:
Zu jedem existiert ein mit f(a)=b.
Man sagt auch: Abbildung von A auf B.
Bijektivität[Bearbeiten | Quelltext bearbeiten]
Eine Funktion ist dann bijektiv, wenn f injektiv und surjektiv ist.
Man sagt auch umkehrbar eindeutig oder eindeutige Abbildung von A auf B ider 1-1 Abbildung von A auf B.
Kardinalität[Bearbeiten | Quelltext bearbeiten]
Für die Kardinalzahl (Kardinalität, Mächtigkeit), einer Menge A schreibt man |A| oder #A und für sie gilt:
- hat eine Menge A nur eindlich viele Elemente (eine endliche Menge), so bezechnet |A| die Anzahl der Elemente von A,
- Allen gleichmächtigen, unendlichen Mengen ordnet man als Kardinalzahl das Symbol "Aleph" zu: