Der Begriff "Vektor" stammt aus der Geometrie und Mechanik.
- In der Geometrie ist ein Vektor eine Klasse von Pfeilen gleicher Länge (Betrag), gleicher Richtung und gleicher Orientierung.

- In der Mechanik symbolisieren Vektoren die Einwirkungen von Kräften.
Verschieben wir eine Ebene zunächst parallel:
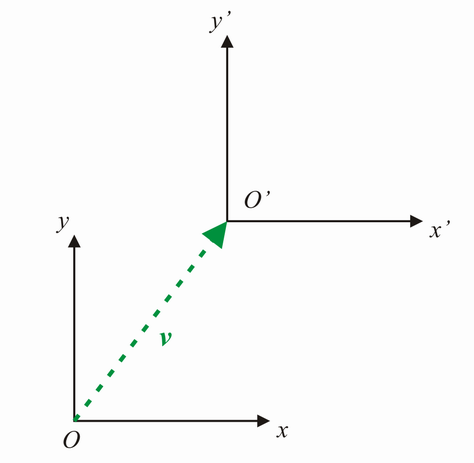
Der Punkt  wird mit dem Achsenkreuz
wird mit dem Achsenkreuz  nach
nach  mit dem Achsenkreuz
mit dem Achsenkreuz  verschoben.
verschoben.
Die Strecke der Verschiebung,  wird Verschiebungsvektor oder kurz Vektor genannt.
wird Verschiebungsvektor oder kurz Vektor genannt.
Was passiert, wenn wir zwei Verschiebungen mit den Verschiebungsvektoren hintereinander ausführen?
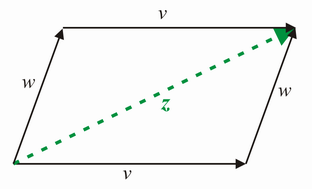
Es entsteht wieder ein Vektor z, der als Summe der Vektoren v und w bezeichnet wird (Parallelogrammgesetz; man beachte die Assoziativität und Kommutativität der Operation!).
Addiert man einen Vektor n Mal, so erhält man den Vektor nv: Einem Vektor derselben Richtung wie v und der n-fachen Länge.
Dieses Additionsgesetz gilt auch für Geschwindigkeiten, Beschleunigungen, Kräfte und ähnliche gerichtete Grössen in dr Mechanik und Physik, welche sich als Vektoren darstellen lassen.
Man kann Vektoren auf diese Art und Weise auch in Komponenten zerlegen.
Basierend auf den Einheitsvektoren  und
und  mit der Länge 1 kann man einen Vektor, an den Achsen orientierend, als
mit der Länge 1 kann man einen Vektor, an den Achsen orientierend, als  und
und  anschreiben. (
anschreiben. ( )
)
Oft verwendet man dann auch für die Gesamtbeschreibung  oder kürzer:
oder kürzer:  .
.
Die Addition zweier Vektoren  und
und  schreibt man dann als:
schreibt man dann als:  .
.
Weitere Begriffe:
- Betrag (Länge) eines Vektors:
 (rechtwinkelige katesische Koordinaten vorausgesetzt, damit Satz von Phytagoras angewendet werden kann)
(rechtwinkelige katesische Koordinaten vorausgesetzt, damit Satz von Phytagoras angewendet werden kann)
- Nullvektor: Betrag ist Null, da

- Einheitsvektor: Betrag ist Eins
Ein euklidischer Raum ist in der Mathematik ein Raum, für den die Gesetze der euklidischen Geometrie gelten. Euklidische Räume existieren in beliebigen Dimensionen n. Ein zweidimensionaler euklidischer Raum heißt auch euklidische Ebene.
Algebraisch lässt sich ein euklidischer Raum in beliebigen Dimensionen n (n > 0) durch das n-fache kartesische Produkt der reellen Zahlenmenge  beschreiben. Da bei dieser Beschreibung keine Informationen verlorengehen, wird der Begriff häufig auf diesen speziellen Raum verengt, der dann als
beschreiben. Da bei dieser Beschreibung keine Informationen verlorengehen, wird der Begriff häufig auf diesen speziellen Raum verengt, der dann als  oder auch
oder auch  bezeichnet wird.
bezeichnet wird.
Ein Euklidischer Raum muss nicht notwendigerweise durch den speziellen Raum  beschrieben werden: Jeder endlichdimensionale Vektorraum, auf dem ein Skalarprodukt definiert ist, das je zwei Vektoren eine reelle Zahl zuordnet, ist zugleich ein Modell eines Euklidischen Raums gleicher Dimension; man bezeichnet einen solchen Vektorraum daher auch als Euklidischen Vektorraum. Allerdings ist durch Auswahl einer Basis jeder Euklidische Vektorraum isomorph zu dem speziellen Raum
beschrieben werden: Jeder endlichdimensionale Vektorraum, auf dem ein Skalarprodukt definiert ist, das je zwei Vektoren eine reelle Zahl zuordnet, ist zugleich ein Modell eines Euklidischen Raums gleicher Dimension; man bezeichnet einen solchen Vektorraum daher auch als Euklidischen Vektorraum. Allerdings ist durch Auswahl einer Basis jeder Euklidische Vektorraum isomorph zu dem speziellen Raum  , das heißt, es gibt zumindest hinsichtlich der Geometrie keine Unterschiede zwischen beiden.
, das heißt, es gibt zumindest hinsichtlich der Geometrie keine Unterschiede zwischen beiden.
Ein Vektor wird dabei definoert als ein System von n geordneten reellen Zahlen  (im folgenden sind
(im folgenden sind  die Basisvektoren):
die Basisvektoren):
- Mögliche Schreibweise:

- kürzer:

Die Addition von Vektoren ist kommutativ und assoziativ und erfolgt durch:

Die Subtraktion ist einfach die Umkehrung der Addionion, wobei a - a den Nullvektor ergibt!
Die Multiplikation eines Vektors mit einem Skalar  (Skalar
(Skalar  )erfolgt durch:
)erfolgt durch:

- 1*a = a, 0*a = 0
Wir befinden uns in  und betrachten:
und betrachten:
- Vektoren:

- Skalare:

Ein Vektor mit der Form  heißt Linearkombination der Vektoren
heißt Linearkombination der Vektoren  .
.
Die Vektoren  heißen linear abhängig, wenn einer von ihnen als Linearkombination der übrigen dargestellt werden kann, d.h. z.B.:
heißen linear abhängig, wenn einer von ihnen als Linearkombination der übrigen dargestellt werden kann, d.h. z.B.: 
Andernfalls heißen  linear unabhängig.
linear unabhängig.
Satz: Die Vektoren  sind genau dann linear unabhängig, wenn gilt:
sind genau dann linear unabhängig, wenn gilt: 
Das innere oder skalare Produkt zweier Vektoren (skalares Produkt) ist ein Skalar (die Operation ist kommutativ und distributiv, ABER NICHT ASSOZIATIV, denn das erste innere Produkt ist ein Skalar!)

Betrachten wir folgende Grafik:
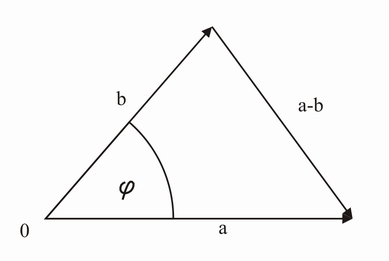
Dabei können wir den Cosinussatz anwenden! Es ergibt sich:

Es gilt ferner:

Wenn a*b = 0 so folgt daraus  - d.h. a und b sind orthogonal zueinander!
- d.h. a und b sind orthogonal zueinander!
In  gilt:
gilt: 
Für  gilt:
gilt:
 wenn
wenn  oder
oder  oder
oder  (parallel)
(parallel)- sonst:
 orthogonal zu
orthogonal zu  ,
, 
- ||
 || = ||
|| = || ||*||
||*|| ||, wobei
||, wobei  der Winkel zwischen
der Winkel zwischen  und
und  ist. Dies ist Fläche des von diesen Vektoren aufgespannten Parallelogramms
ist. Dies ist Fläche des von diesen Vektoren aufgespannten Parallelogramms
 ,
, ,
, bilden ein Rechtssystem (3-Finger-Regel, rechte Hand)
bilden ein Rechtssystem (3-Finger-Regel, rechte Hand)

3 Determinanten, wobei gilt: Determinante aus 
Es gelten folgende Rechengesetze:


 ,
,  (Distributivgesetz)
(Distributivgesetz)
 - Graßmannscher Entwicklungssatz
- Graßmannscher Entwicklungssatz - Lagrang'sche Identität
- Lagrang'sche Identität
 http://de.wikipedia.org/wiki/Vektor
http://de.wikipedia.org/wiki/Vektor
 http://de.wikipedia.org/wiki/Euklidischer_Raum
http://de.wikipedia.org/wiki/Euklidischer_Raum


