TU Wien:Mathematik 1 VO (Drmota)/Prüfung 2009-07-02

Angabe

vom Gleichnamigen Thread im Informatik-Forum f.thread:74294, Gruppe A und B waren vermutlich nur von der Reihenfolge her anders!

Beispiel 1 (Induktion)

Anhand der folgenden Formel ist die vollständige Induktion zu erklären:

$\cos(x)*cos(2x)*cos(4x)*...*cos(2^{n}x)={\frac {\sin(2^{n+1}x)}{2^{n+1}\sin(x)}}$

Hinweis: $\sin(2x)=2\sin(x)\cos(x)$

Beispiel 2 (Graphentheorie)

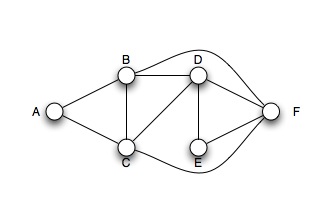
Gegebn ist folgende Adjazentenmatrix:

$A(G)={\begin{pmatrix}0&1&1&0&0&0\\1&0&1&1&0&1\\1&1&0&1&0&1\\0&1&1&0&1&1\\0&0&0&1&0&1\\0&1&1&1&1&0\end{pmatrix}}$

• Skizzieren Sie den Graphen G.
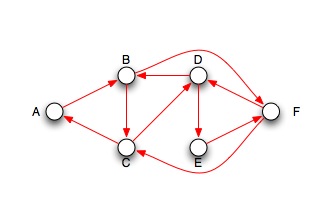
• Geben Sie die geschlossene eulersche Linie an (sofern vorhanden)
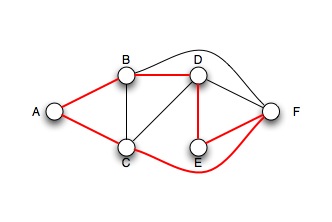
• Geben Sie die geschlossene hamiltonsche Linie an (sofern vorhanden)
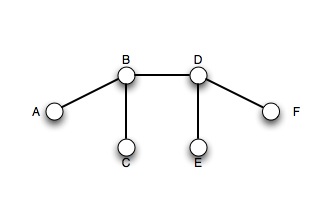
• Geben Sie einen spannenden Baum des Graphen an.

Beispiel 3 (Matrizenoperationen)

Gegeben ist die Matrix:

$A={\begin{pmatrix}1&3&0\\0&1&4\\1&2&-5\end{pmatrix}}$

• Bestimmen Sie die Determinante det(A).
• Bestimmen Sie, sofern vorhanden, $A^{-1}$ - die inverse Matrix zu A.
• Bestimmen Sie, ohne weitere Rechnung:
  • det$((A^{3})^{-1})$ und
  • $(A^{T})^{-1}$

Beispiel 4 (Theorie Folgen & Reihen)

Wann ist eine Reihe Konvergent? Wie lautet das Leibniz-Kriterium?

Untersuchen Sie folgende Reihen auf Konvergenz:

$\sum _{n\geq 0}^{\infty }({\frac {5}{6}})^{n}$

$\sum _{n\geq 1}^{\infty }{\frac {3}{n}}$

$\sum _{n\geq 1}^{\infty }{\frac {(-1)^{n}}{n}}$

Beispiel 5 (Theorie Algebraische Strukturen)

• Wie lautet die Definition für eine Gruppe? Genaue Erklärung.
• Geben Sie je ein Beispiel für eine endliche Gruppe und eine unendliche Gruppe an.
• Geben Sie ein Beispiel für eine algebraische Struktur (mit binärer Operation) an, die keine Gruppe ist.

Ausarbeitung

Beispiel 1 (Induktion)

• Induktionsanfang n=0

$cos(x)={\frac {sin(2*x)}{2*sin(x)}}={\frac {2*sin(x)*cos(x)}{2*sin(x)}}=cos(x)$

• Induktionsschritt

$\prod _{k=0}^{n+1}cos(2^{k}x)=\prod _{k=0}^{n}cos(2^{k}x)*cos(2^{n+1}x)$

${\frac {sin(2^{n+2}*x)}{2^{n+2}*sin(x)}}={\frac {sin(2^{n+1}*x)}{2^{n+1}*sin(x)}}*cos(2^{n+1}*x)$

${\frac {sin(2^{n+2}*x)}{2}}=sin(2^{n+1}*x)*cos(2^{n+1}*x)$

$sin(2*2^{n+1}*x)=2*sin(2^{n+1}*x)*cos(2^{n+1}*x)\rightarrow$ Hinweis aus Angabe, mit $x:=2^{n+1}*x$

--Anwesender 21:49, 3. Jul. 2009 (CEST)

Beispiel 2 (Graphentheorie)

Lösung von --Mhaslhofer 10:53, 4. Jul. 2009 (CEST)

${\begin{pmatrix}&A&B&C&D&E&F\\A&0&1&1&0&0&0\\B&1&0&1&1&0&1\\C&1&1&0&1&0&1\\D&0&1&1&0&1&1\\E&0&0&0&1&0&1\\F&0&1&1&1&1&0\end{pmatrix}}$

• Skizze

• eulersche Linie (A->B->F->D->B->C->D->E->F->C->A)

• hamiltonsche Linie

• spannender Baum

Beispiel 3 (Matrizenoperationen)

$A={\begin{pmatrix}1&3&0\\0&1&4\\1&2&-5\end{pmatrix}}$

Determinante: $-5+3*4+0-0-8-0=12-8-5=-1$

$A^{-1}={\begin{pmatrix}13&-15&-12\\-4&5&4\\1&-1&-1\end{pmatrix}}$

$A^{-1^{T}}=A^{T^{-1}}={\begin{pmatrix}13&-4&1\\-15&5&-1\\-12&4&-1\end{pmatrix}}$

$det(A^{3^{-1}})=det(A)^{3^{-1}}={(-1)^{3}}^{-1}=-1$

--Anwesender 22:54, 3. Jul. 2009 (CEST)

Beispiel 4 (Theorie Folgen & Reihen)

• Wann ist eine Reihe Konvergent?

• Wie lautet das Leibniz-Kriterium?

• Untersuchen Sie folgende Reihen auf Konvergenz:
  • $\sum _{n\geq 0}({\frac {5}{6}})^{n}$
    • Lösung von Anwesender
      • konvergent, Wurzelkriterium
      • ${\sqrt[{n}]{({\frac {5}{6}})^{n}}}={\frac {5}{6}}\leq 1$
    • Lösung von Mhaslhofer
      • $({\frac {5}{6}})^{n}=q^{n}\;mit\;q\,<\,1$
      • Das ist dann eine geometrische Reihe, und die konvergiert für q<1

• • $\sum _{n\geq 1}{\frac {3}{n}}$
    • divergent, Harmonische Reihe (Buch S. 149/150) --Mhaslhofer

• • $\sum _{n\geq 1}{\frac {(-1)^{n}}{n}}$
    • konvergent, Leibnizkriterium --Anwesender

Beispiel 5 (Theorie Algebraische Strukturen)

Lösung von --Mhaslhofer 21:21, 3. Jul. 2009 (CEST)

• Die Kriterien für eine Gruppe (G,$\circ$) sind:

1. Abgeschlossenheit bezüglich der binären Operation $\circ$
   daher: $\forall \,a,b\;\epsilon \,G:\;a\circ b\;\epsilon \,G$
2. Die binären Operation $\circ$ ist assoziativ
   daher: $\forall \,a,b,c\;\epsilon \,G:\;a\circ (b\circ c)=(a\circ b)\circ c$
3. Existenz eines (links-)neutralen Elements $e$
   daher: $\exists \;e\;\epsilon \,G:\;e\circ a=a\;\forall \;a\,\epsilon \,G$
4. Existenz (links-)inverser Elemente
   daher: $\forall \;a\,\epsilon \,G\;\exists \,a':\;a'\circ a=e$

• Beispiel für eine endliche Gruppe: $(\mathbb {Z} _{3},+)$
• Beispiel für eine unendliche Gruppe: $(\mathbb {Z} ,+)$
• Beispiel für eine algebraische Struktur, die keine Gruppe ist: $(\mathbb {Z} ,*)$ wobei $*$ die "normale" Multiplikation ist.
  Bei $(\mathbb {Z} ,*)$ fehlen dann die meisten inversen Elemente.