TU Wien:Mathematik 1 VO (Panholzer)/Stoff WS05/4. VO 19.10.2005
Weiteres zu Q
ist abzählbar unendlich - dies wird durch die Cantor-Diagonalisierung bewiesen:
Die Aussage ist, dass die natürlichen Zahlen und die positiven Brüche gleichmächtig sind.
Dies lässt sich zeigen, indem man die Brüche folgendermaßen in einem zweidimensionalen Schema anordnet:
1/1 1/2 1/3 1/4 1/5 ...
2/1 2/2 2/3 2/4 2/5 ...
3/1 3/2 3/3 3/4 3/5 ...
4/1 4/2 4/3 ...
5/1 5/2 ...
...
und dieses Schema dann 'diagonal' durchläuft (abzählt), wobei man kürzbare Brüche überspringt:
1.-> 2. 5.-> 6. 11. -> ...
/ / / /
/ / / /
3. (-) 7. (-)
| / / /
| / / /
4. 8. (-)
/ /
/ /
9. (-)
| /
| /
10.
Man erhält auf diese Weise eine Abzählung der positiven rationalen Zahlen:
- 1, 1/2, 2, 3, 1/3, 1/4, 2/3, 3/2, 4, 5, 1/5, ...
Durch das Überspringen kürzbarer Brüche liegt für jede positive rationale Zahl genau ein Repräsentant (der nicht mehr kürzbare Bruch) in dieser Abzählung, wodurch die gewünschte Bijektion hergestellt ist.
Um die Gleichmächtigkeit aller rationalen Zahlen und der natürlichen Zahlen zu zeigen, erweitert man diese Abzählung. Vor die Eins fügt man eine Null ein und hinter jeder Zahl deren Negatives:
- 0, 1, -1, 1/2, -1/2, 2, -2, 3, -3, 1/3, -1/3, 1/4, -1/4, 2/3, -2/3, ...
Man erhält damit eine Bijektion zwischen den rationalen und den natürlichen Zahlen, was gleichbedeutend mit der Gleichmächtigkeit beider Mengen ist.
Mengen, welche gleichmächtig zu irgendeiner Teilmenge der natürlichen Zahlen sind, heißen abzählbar (bzw. höchstens abzählbar). Mengen, welche gleichmächtig zu einer beschränkten Teilmenge der natürlichen Zahlen sind, sind endlich. Mengen, welche gleichmächtig zur Menge der natürlichen Zahlen sind, heißen abzählbar unendlich (bzw. abzählbar).
Somit gilt:
Und es gilt auch: ... "Continuum"
Darstellung der reellen Zahlen
Darstellung im Dezimalsystem:
(gewollt trivial, denn )
Wähle Basis
=
- b = 2 - Binärsystem
- b = 16 - Hexadezimalsystem
Umrechnung: - gefragt ist .
126 : 2 = 63 +0R
63 : 2 = 31 +1R
31 : 2 = 15 +1R
15 : 2 = 7 +1R
7 : 2 = 3 +1R
3 : 2 = 1 +1R
1 : 2 = 0 +1R
ergibt sich aus:
usw. fld.
Maschinenzahlen M
Darstellung:
M ... Mantisse, E ... Exponent
weil nur endlichen Bereich auf der Zahlengerade umfassend - Richtung Minimum/Maximum immer weniger dicht verteilt.
R ist überabzählbar
ist überabzählbar. Der Beweis erfolgt indirekt.
Angenommen wird, dass abzählbar ist
Abzählbarkeit aller (Intervall 0,1)
wähle Binärdarstellung:
Konstruiere Zahl folgendermaßen:
- k-te Nachkommastelle wählen
nicht abzählbar
Komplexe Zahlen
Quadratische Gleichung:
Hat Lösungen:
Diskriminante:
- D > 0 verschiedene reelle Lösungen
- D = 0 genau eine Lösung
- D < 0 keine reelle Lösung
Gauß'sche Darstellung der komplexen Zahlen:
- Realteil
- Imaginärteil
- i = imaginäre Einheit
Kartesische Darstellung:
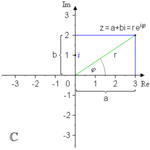
Rechnen mit komplexen Zahlen:
Websites
- http://de.wikipedia.org/wiki/Rationale_Zahl
- http://de.wikipedia.org/wiki/Cantor-Diagonalisierung
- http://de.wikipedia.org/wiki/Hilberts_Hotel
- http://de.wikipedia.org/wiki/Reelle_Zahlen
- http://de.wikipedia.org/wiki/Dualsystem
- http://de.wikipedia.org/wiki/Hexadezimalsystem
- http://de.wikipedia.org/wiki/Maschinenzahl
Komplexe Zahlen
- http://de.wikipedia.org/wiki/Komplexe_Zahlen
- http://www.soc.tuwien.ac.at/courses/dsp/2005/DSP_2-KomplexeZahlen.pdf - Vortragsfolie komplexe Zahlen von Prof. Grünbacher
- http://www.soc.tuwien.ac.at/courses/dsp/2005/KomplexeZahlen.pdf - Artikel von Prof. Grünbacher zu komplexen Zahlen
- http://www.soc.tuwien.ac.at/courses/dsp/2005/B-1_Komplexe_Zahlen.TXT - Komplexe Zahlen in MATLAB (Prof. Grünbacher)
- http://www.soc.tuwien.ac.at/courses/dsp/2005/KomplDarstellung.zip - Kartesische Darstellung der komplexen Zahlen (Prof. Grünbacher)