TU Wien:Mathematik 1 VO (Panholzer)/Stoff WS05/8. VO 31.10.2005

Mengen - Relationen (Forts.)

$A_{1}x,...,xA_{n}:=\{(a_{1},...,a_{n}):a_{i}\in A_{i},\forall 1\leq i\leq n\}$

kartesischer Begriff der Mengen $A_{1},...,A_{n}$

$A:=A_{1}:=A_{2}=...=A_{n}\Rightarrow A\times A\times ...\times A=:A^{n}$ (n Mal kartes. Prod.)

$\mathbb {R} ^{2}=\mathbb {R} \times \mathbb {R} ,\mathbb {R} ^{3},\mathbb {R} ^{n}$

A = {0,1}, $A^{3}=A\times A\times A$ = {(0,0,0), ... , (1,1,1)}

(Würfel)

Definition: Unter einer zweistelligen (=binären) Relation zwischen den Mengen A und B versteht man eine Teilmenge des kartesischen Produktes von A und B, d.h. $R\subseteq A\times B$. Insbesondere wenn A = B, dann heißt R eine binäre Relation auf A, $R\subseteq A^{2}.$. Statt $(a,b)\in R$ schreibt man meist a R b.

Beispiel: Endliche Mengen

A={1,2}, B={3,4,5}

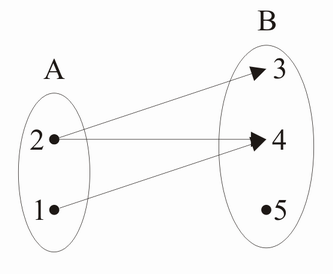
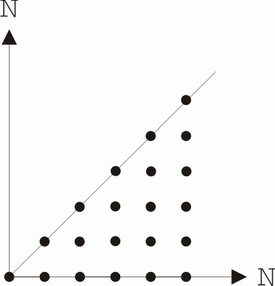
Weiters Bsp.: A = B = $\mathbb {N} ,aRb:\Leftrightarrow a\leq b$

(natürliche Ordnung auf $\mathbb {N}$

R = {(0,0), (0,1), (0,2), (1,1), (1,2), ....)}

Definition: Unter einer n-stelligen Relation zwischen den Mengen $A_{1},...,A_{n}$ versteht man eine Teilmenge von $A_{1}\times ...\times A_{n}$, d.h. $R\subseteq A_{1}\times ...\times A_{n}$

Falls $A:=A_{1}=...=A_{n}$, dann heisst $R\subseteq A^{n}$ eine n-stellige Relation auf A.

Beispiel: Relationale Datenbanken

Spezielle Relationen

Sei R eine binäre Relation auf A.

$R\subseteq A^{2}$

Betrachte $G_{R}$ zugehöriger Graph der Relation R:

• Knoten: Elemente von A
• gerichtete Kanten: eine gerichtete Kante verläuft von a nch b. g.d.w. a R b. $\forall (a,b)\in R$

A = {a,b,c,d}

R = {(a,a), (b,b), (a,b), (b,a), (a,c), (d,c)}

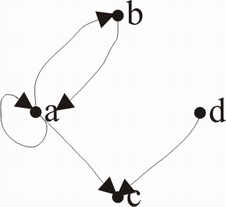
Definition: Sei R eine binäre Relation auf A. Dann heißt die Relation R

• (R) reflexiv, falls a R a, $\forall a\in A$
• (S) symmetrisch, falls: a R b $\Rightarrow$ b R a, $\forall a,b\in A$
• (A) antisymmetisch, falls: a R b $\wedge$ b R a $\Rightarrow$ a = b, $\forall a,b\in A$
• (T) transitiv, falls a R b $\vee bRc\Rightarrow aRc,\forall a,b,c\in A$

Falls für eine Relation R die Eigenschaften (R),(S) und (T) gelten, dann heisst R eine Äquivalenzrelation auf A.

Falls für eine Relation R die Eigenschaften (R), (A) und (T) gelten, dann heisst R eine Halbordnungsrelation auf A.

Betrachte $A=\mathbb {Z} ,aRb:\Leftrightarrow a\equiv b{\text{ mod 3 }}$

Ist (R), (S), nicht antisymmetisch, (T)

$\Rightarrow$ Äquivalenzrelation auf $\mathbb {Z}$

A = P(M) .... Potenzmenge einer Menge M

$M_{1}RM_{2}:\Leftrightarrow M_{1}\subseteq M_{2}$

Ist: (R), nicht symmetrisch, (A) da $M_{1}\subseteq M_{2}\wedge M_{2}\subseteq M_{1}\Rightarrow M_{1}=M_{2}$, (T)

A = $\mathbb {N} \qquad \leq$ natürliche Ordnung auf $\mathbb {N}$

Ist (R), (A), (T) $\Rightarrow$ Halbordungsrelation $\leq$

Es gilt weiters: für $a,b\in \mathbb {N}$ gilt: $a\leq b\vee b\leq a$. Je zwei Elemente sind vergleichbar $\Rightarrow$ Vollordnung (Kette)

• Allrelation: $\alpha =R=A^{2}$ (Graph) (R) (S) (T)
• Identische Relation: $\epsilon =R=:\{(a,b),a\in A\}$